Раздел 9. «Раскраски графа».

1. Необходимые определения и формулировки теорем.

   1. В чем состоит задача о раскраске вершин графа?

   2. Каков алгоритм решения задачи о раскраске графа?

   3. В чем состоит задача о раскраске ребер графа?

   4. Что Вы знаете о хроматическом индексе?

2. Задачи для усвоения материала.

1. Для каждого из предложенных графов найдите правильные раскраски рёбер и вершин.

Здесь, к сожалению, придется рисунки переделать вручную: номера их какие-то странные, на некоторых рисунках уже построены правильные раскраски.

]

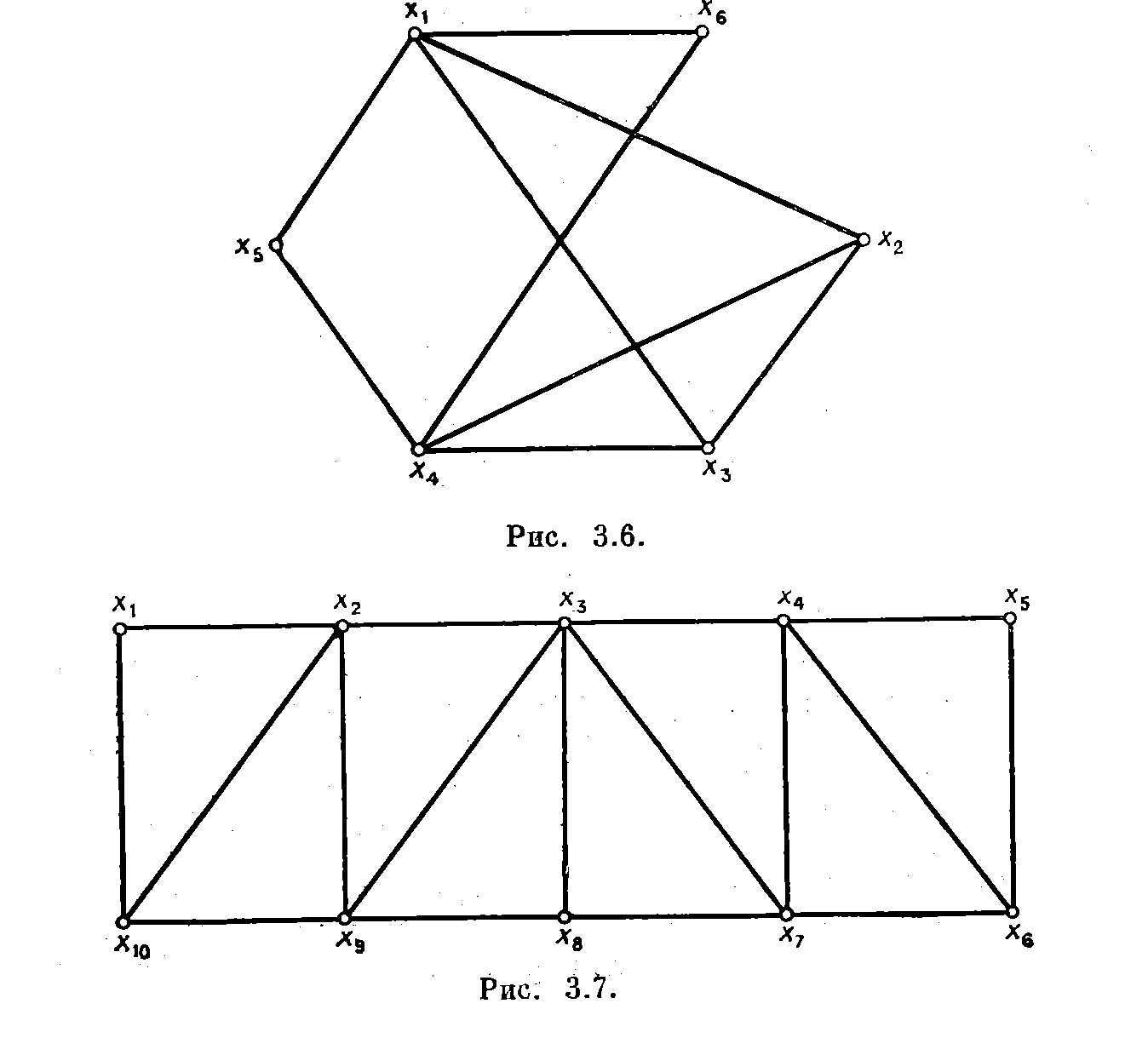
Итоговое повторение темы 2. Контрольная работа № 2.

1. Основные вопросы.

1. Что такое орграф, граф, вершина, дуга, ребро, путь, цепь, контур, цикл?

2. Каков алгоритм решения задачи о кратчайшем пути в невзвешенном графе?

3. Каков алгоритм решения задачи о кратчайшем пути во взвешенном графе?

4. Что такое эйлерова цепь (цикл), у каких графов они существуют?

5. В чем состоит формула Эйлера и для каких объектов она верна?

6. Как выглядят непланарные графы № 1, № 2, типов 1, 2 и в чем состоит теорема Куратовского-Понтрягина?

7. Что такое хроматическое число графа и что Вы знаете о его величине?

8. Что такое хроматический индекс графа и что Вы знаете и о его величине?

2. Контрольная работа.

Вариант 0

1. Вопрос по теории.

2. Обладает ли эйлеровой цепью (или эйлеровым циклом) следующий граф?

3. Является ли данный граф плоским? (планарным)

4. Считая данный граф планарным, определить количество его граней.

5. Дан граф:

Найти кратчайший путь из точки в точку В (в смысле наименьшего количества рёбер).

6. Дан граф.

B

A

а) Превратить его во взвешенный, используя следующие данные

б) Найти кратчайший путь из точки в точку В (в смысле наименьшей суммы весов).

7. Найти хроматическое число графа

Тема 3. Приложения теории графов

Раздел 10. «Матрицы смежности и инццдентности. Код Харари».

1. Необходимые определения и формулировки теорем.

   1. Что такое матрица смежности орграфа?

   2. Каким свойством обладает матрица смежности неориентированного графа?

   3. Что такое матрица инцидентности оргрфа?

   4. Как строится код Харари?

   5. Какая нумерация вершин графа считается канонической?

2. Задачи для усвоения материала.

ПРЕДСТАВЛЕНИЕ ГРАФОВ МАТРИЦАМИ

1. Написать матрицу смежности данного орграфа

.

2. Восстановить граф по матрице смежности .

3. В условиях задачи 10.2 найти число путей длины 3 из 1-й вершины в 4-ю.

4. Написать матрицу инцидентности данного орграфа

.

ПРЕДСТАВЛЕНИЕ ГРАФОВ КОДАМИ

5. Найти код Харари графа .

6. Восстановить граф по коду Харари а) 26; б) 794; в) 14400.

7. Существует ли граф с кодом Харари 282 ?