1. Идеальная и реальная жидкости и их основные физические свойства.

Идеальная жидкость- абсолютно не сжимаемая, не обладающая внутренним трением между частицами ,и не изменяющая свой обьем при изменении температуры .

Реальная жидкость- это такая жидкость которая имеет внутреннее трение чистиц и теряющая энергию . так как реальная жидкость имеет внутреннее трение при расчете нужно учитывать потери.

1.Плотностью жидкости называют массу жидкости заключенную в единице объема.

Плотность жидкостей зависит от температуры и практически не зависит от давления.

Абсолютная плотность – представляет собой отношение плотности рассматриваемого вещества к плотности другого вещества ( чаще это вода ) при определенных физических условиях. Плотность газов значительно изменяется с изменением давления и температуры. 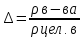формула плотности газа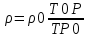

2.Вязкость жидкости - свойство жидкости сопротивляться скольжению или сдвигу ее слоев.(рисунок) При движении реальной жидкости, вследствие неравенства скоростей частиц , в ней возникают силы внутреннего трения.. Суть ее заключается в возникновении внутренней силы трения между движущимися слоями жидкости, при ее течении , прямо пропорционально градиенту скорости и определяется по формуле Ньютона

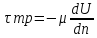
Где 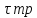– напряжение внутреннего трения (напряжение сдвига или касательное напряжение)

μ- динамический коэффициент вязкости, или сила вязкостного трения, dU /dn - градиент скорости, характеризующий изменение скорости , проходящееся на единицу расстояния по нормали между слоями.

Знак «-» указывает на то , что касательное напряжение тормозит слой , движущийся с относительно большой скоростью.

С увеличение температуры вязкость уменьшается , газы уменьшаются. При увеличении давления и температуры 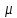для капельных жидкостей уменьшается.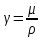[м²/с]

3. Сжимаемость - свойство жидкости изменять свой объем под действием давления. Сжимаемость жидкости характеризуется коэффициентом объемного сжатия, который определяется по 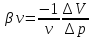[Па^-1] «_» потому что, при увеличении давлений, объем уменьшается 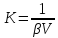– модуль упругости.

4. Температурное расширение . увеличение температуры приводит к росту объема жидкости. Характеризуется коэффициентом объемного расширения , который представляет собой относительное изменение объема при изменении температуры на 1 градус

(К^-1)

При изменении температуры в небольших интервалах принимают

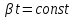
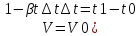Поскольку для капельных жидкостей коэффициент температурного расширения ничтожно мал, то при практических расчетах его не учитывают.

5. Поверхностное натяжение - в ряду процессов в химической технологии жидкость соприкасается с другой жидкостью , практически не смешивается с первой. Поверхность раздела стремится к меньшему , соответственно капли жидкости взвешенные в другой жидкости принимают форму шара. Силы поверхностного натяжения всегда направлены ко внутренне нормально рассматриваемой площадке (рис)

Поверхностное натяжение характеризует работу, которую необходимо затратится для увеличения поверхности натяжения.( Рисунки ) для увеличения поверхности натяжения надо добавить ПАВ

2.гидростатическое давление и его основные свойства. Понятие абсолютного давления, избыточного давления , вакуума. Единицы измерения.. Абсолютным (полным, барометрическим) называют давление, отсчитываемое от абсолютного нуля, т. е.истинное давление. Оно может быть как выше, так иниже атмосферного. Если абсолютноедавление ниже атмосферного, его называютостаточным. Если абсолютное давление больше атмосферного разность абсолютного и атмосферного давления называют избыточным манометрическим давлением . если абсолютное давление меньше атмосферного вероятность атмосферного и абсолютного давления называется разрежение, вакуум или вакуумметрическое давление. вакуум - это недостаток до атмосферного давления. Для измерения давления используют барометр и манометр и вакуумметры. В СИ давление измеряется в Па . один паскаль равен в силе в 1Н, действующей на поверхность площадью в 1м². Атмосферное давление это гидростатическое давление столба воздуха , которое на уровне моря равнозначно давлению столбика ртути высотой h₀=760мм и равно 1011325Па. Давление изменяется в разных единица. Между единицами давления существует следующее соотношение: 1атм(физическая атмосфера)= 760мм рт ст = 1,013*10⁵Па=10,33мводст= 1,033кгс/см².; 1 кгс/см²=1ат (техническая атмосфера) = 10⁴ кгс/м²=9,81*10⁴Па=735,6ммртст=10мводст

3. Основное уравнение гидростатики в дифференциальной форме. Поверхности равного давления.

Соотношение между силами действующими на жидкость , находящихся в состоянии относительного покоя выражаются диффиринциальным уравнением Эйлера . в жидкости выделим элементарный объем в покоящейся жидкости в виде параллелепипеда (рисунок) . на выделенный параллелограмм действуют поверхностные массовые силы P= f(x,y,z) . массовые силы действующие со стороны жидкости на выделенный элементарный объем со стороны х будут x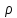dxdyzdz- проекция массовой силы вдоль оси х. изменение давления вдоль оси

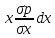
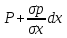гидростатическое давление .

Действующая со стороны жидкости на правую грань параллелепипеда .

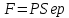
Сила направлена на левую грань

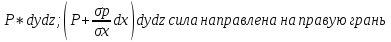
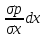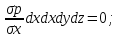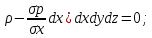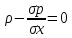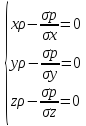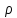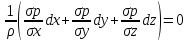Согласно основному принципу статики сумма проекции всех сил( на координатной плоскости) равно 0. В противном случае происходило бы смещение жидкости. Сумма проекции всех сил ( массовых и поверхностных) x*pdxdydz+pdydz-(p+)dydz=0; x*pdxdydz-(xx- Сумма проекций всех сил действующих со стороны жидкости в доль оси х. Разделив все члены на и умножим на dx, dy, dz после сложения получим xdx+ydy+zdz- по скольку давление является функцией на оси координат , то выражение в () полное диффиринциальное давление давления получим xdx+ydy+zdz- 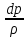=0

Dp= (xdx+ydy+zdz) основное уравнение в диффиринциальной форме.

Поверхность, все точки которой испытывают одинаковое давле­ние, называются поверхностью равного давления.

4. Равновесие жидкости в поле силы тяжести. Основное уравнение гидростатики в интегральной форме. Закон Паскаля. Понятие геометрического и пьезометрического напоров.

Равновесие жидкости в поле тяжести .Из условия равновесия жидкости в поле тяжести следуют два утверждения:

1) давление во всех точках, лежащих в одной горизонтали, одинаково;

2) при увеличении глубины на h давление возрастает на величину .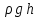

Таким образом, если давление на свободной поверхности жидкости равно P₀, то на глубине h будем иметь давление P(h)=P₀+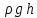

Давление P₀ называют внешним давлением, а член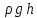– давлением столба жидкости.

Закон Архимеда. На тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх и равная численно весу вытесненной жидкости,

F_A=.

Основное уравнение гидростатики в интегральной форме

Если на жидкость из массовых сил действует только сила тяжести то Z=-g, a X=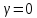тогда

dp= -.

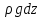Последняя зависимость показывает, что при действии только сил тяжести давление в покоящейся жидкости меняется только по вертикали. при интегрировании для двух горизонтальных поверхностей 1и 2 P₂- P1= (z₁-z₂)*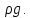 или z₁+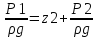Полученную зависимость называют основным уравнением гидростатики в интегральной форме.

Плоскость сравнения -это горизонтальная плоскость проведенная на произвольный высоте . Напором в гидравлике называют удельную энергию жидкости (энергию жидкости относительную единице веса). Следовательно, Согласно основному уравнение гидростатики, для каждой точке покоящейся жидкости сумма геометрической и пьезометрического напора является величиной постоянной.

С энергетической точки зрения геометрический напор представляет удельную энергии потенциальной энергии положения данной точки над выбранной плоскости сравнения, а пьезометрический напор потенциальную энергию давления в этой точке. 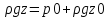Сумма указанных напоров равна общей Удельной потенциальной энергии или гидростатическому напору жидкости основное уравнение гидростатики представляет собой частный случай закона сохранения энергии : Удельная потенциальная энергия во всех точках покоящейся жидкости есть величина постоянная : z+илиp+илиp=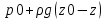обозначена черезh=(z0-z) получим p=p0+ .h- глубина погружения рассматриваемой точки жидкости .

Последнее уравнение является выражением закона Паскаля еще одна запись основного уравнения гидростатики в интегральной форме согласно которому давление создаваемое на поверхности жидкости передается во всех точках жидкости одинаково.