Теория массового обслуживания (ТМО) / Конспект лекций по ТМО / TEMA3~1

Однокальная СМО с отказами.

Проанализируем функционирование одноканальной СМО с отказами. Пусть СМО включает в себя только один канал (n = 1), и на ее вход подается пуассоновский поток заявок П_вх, интенсивность¹ которого in П_вх = λ. В общем случае интенсив­ность входящего потока может изменяться во времени, быть, таким образом, функцией времени t; чтобы это подчеркнуть, вместо λ пишут λ (t).

Заявка, поступившая на вход в момент, когда канал занят обслуживанием, получает отказ и покидает систему.

Пусть (непрерывная) случайная величина T_об— время об­служивания каналом одной заявки — распределена по показа­тельному закону:

с параметром μ.

Поток обслуживании (П_об), — поток обслуженных каналом заявок при условии, что канал не простаивает, т.е. занят об­служиванием непрерывно: по окончании обслуживания оче­редной заявки канал сразу же приступает к обслуживанию сле­дующей.

Таким образом, время обслуживания каналом одной заявки Т_об является интервалом времени между двумя соседними со­бытиями в потоке обслуживании П_об.

Из формулы (3.1) следует (см. [5], с. 74), что поток обслу­живании П_об является простейшим² с интенсивностью μ: in П_об = μ. Интенсивность μ потока обслуживании П_об есть производительность канала. Имеет место равенство: где - среднее время обслуживания одной заявки, относя­щееся только к обслуженным заявкам, т.е. математическое ожидание М[Т_об] случайной величины Т_об (см. [5], с. 74).

Поток обслуживании П_об не следует путать с реальным вы­ходящим потоком П_вых обслуженных каналом заявок, поскольку в последнем интервал времени между двумя соседними об­служенными заявками может включать в себя кроме времени обслуживания и время простоя канала.

Состояния СМО будем характеризовать простаиванием или занятостью ее канала. Тогда СМО может находиться в одном из двух состояний: s₀ — канал свободен (простаивает); s₁ — ка­нал занят.

Переход системы из состояния s₀ в состояние s₁ происходит под воздействием входящего потока заявок П_вх, а из состояния s₁ в состояние s₀ систему переводит поток обслуживании П_об: если в данный момент времени система находится в некотором состоя­нии, то с наступлением первого после данного момента времени события этого потока система тут же «перескакивает» в другое состояние (см. [5], с. 114). Плотности вероятностей перехода¹ из состояния s₀ в состояние s₁ и обратно равны соответственно λ и μ ([5], с. 114). Поэтому размеченный граф² состояний системы имеет вид, указанный на рис. 3.1.

Так как входящий поток заявок и поток обслуживании, пе­реводящие СМО из состояния в состояние, являются пуассоновскими, то в ней протекает марковский случайный процесс (см. |5], с. 114) с дискретными состояниями и непрерывным временем), который, учитывая структуру графа состояний (см. рис. 3.1.), является одновременно и циклическим процессом¹ и процессом «гибели и размножения»².

рис. 3.1.

Обозначим через p_o(t) и p₁(t) — вероятности событий, со­стоящих в том, что в момент времени t СМО находится соот­ветственно в состояниях s₀ и s₁. Эти вероятности называются вероятностями состояний (см. [5], с. 42). Очевидно, что вероят­ности состояний для любого момента времени t удовлетворяют нормированному условию

(см. [5], с. 42).

Вероятности состояний p_o(t) и p₁(t) являются основными характеристиками случайного процесса, протекающего в СМО. Так как этот процесс марковский, то вероятностные функции времени p_o(t) и p₁(t) можно найти из

системы дифференциаль­ных уравнений Колмогорова¹:

составляемой по одному из правил, данных в [5], с. 45, 46.

В силу нормировочного условия (3.2) уравнения системы (3.3) зависимые, и потому одно из них, например второе, мож­но отбросить.

Из условия (3.2):

Подставив выражение (3.4) в первое уравнение системы (3.3), получим дифференциальное уравнение

с неизвестной функцией p_o(t). Это уравнение будем решать при естественном предположении, что в начальный момент време­ни t=0 канал был свободен и, следовательно, начальные усло­вия будут выглядеть так:

Для упрощения решения уравнения (3.5) предположим так­же, что входящий поток заявок П_вх - простейший, т.е. что пуассоновский поток П_вх является к тому же стационарным. Это означает, что интенсивность λ потока П_вх не изменяется с течением времени, т.е. является постоянной: λ = const. В этом случае (см. [5], с. 74), где - среднее время простаивания (свободного состояния) канала или, что то же самое, средний интервал времени между любыми двумя соседними заявками, поступающими на вход СМО (т.е. математическое ожидание М [Т_пр] непрерывной случайной величины Т_пр, пред­ставляющей собой интервал времени между любыми двумя соседними заявками во входящем потоке П_вх).

Уравнение (3.5) представляет собой линейное дифференци­альное уравнение первого порядка с постоянными коэффици­ентами. Из теории дифференциальных уравнений (например, см. [14], с. 56) известно, что общее решение такого уравнения имеет вид:

Отсюда

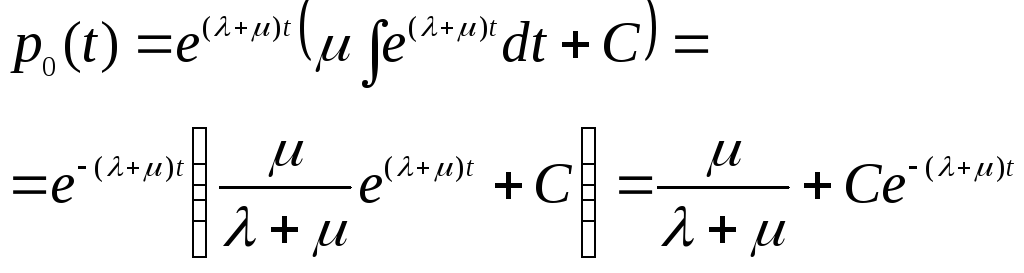
Подставим в равенство (3.7) первое из начальных условий (3.6) p₀(t)=1, получим

, откуда

С учетом найденного значения С равенство (3.7) примет вид

Тогда из равенства (3.4):

Итак, частным решением системы (3.3), удовлетворяющим начальным условиям (3.6), является:

Так как , то функция р₀(t) убывает. А так как , то функция р₀(t) выпукла вниз.

Аналогично из того, что , мы делаем вывод о возрастании функции р₁(t), а из того, что , следует, что функция р₁(t) выпукла вверх.

При t = 0 из системы (3.8) находим: , что соответствует начальным условиям (3.6). Так как из первого уравненеия системы (3.8)

,

то прямая является горизонтальной асимптотой графика функции p₀(t). Аналогично из второго уравнения системы (3.8)

и поэтому прямая является горизонтальной асимптотой графика функции р₁(t).

Рассмотрим три случая:

Случай 1:

Случай 2:

Случай 3:

Построим в одной системе координат графики функций p_o(t) и p₁(t) .

Случай 1. Так как >0, то , т. е. прямая лежит выше прямой и обе лежат в верхней полуплоскости. Поэтому графики функций p_o(t) и p₁(t) пересекаются и пересекают соответственно прямые и . Асимптота отстоит от прямой у = 1 на расстоянии , т.е. на та­ком же расстоянии, что и асимптота от горизон­тальной оси координат. Абсциссу t₁ точки А пересечения гра­фика функции p₀(t) с прямой находим из уравнения :

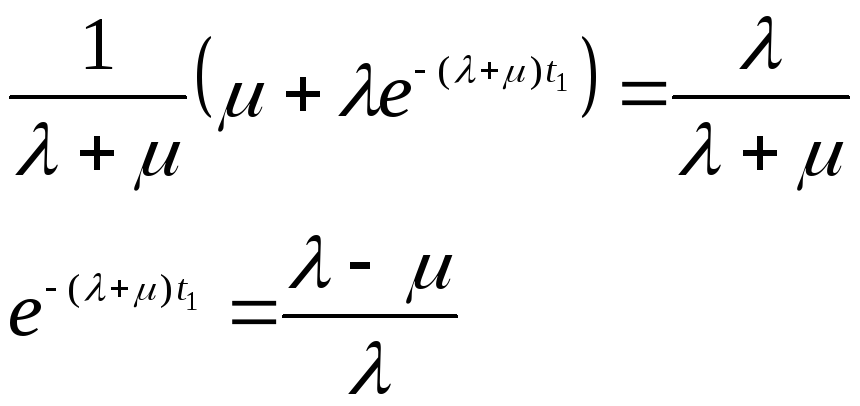
прологарифмировав это равенство, получим

откуда

Отметим, что в силу неравенства отношение >1 и ln существует и больше 0, а следовательно, t₁> 0.

Аналогичным образом из уравнения нахо­дим абсциссу точки В пересечения графика функции p₁(t) с прямой и убеждаемся, что она равна абсциссе t_i (рис. 3.2). Таким образом, точки А и В лежат на одной вертикали/

Теперь найдем абсциссу t₂ точки С пересечения графиков функций p_o(t) и p₁(t). Так как, то из нормировоч­ного условия (3.2) заключаем, что = 1/2. Тогда t₂ можно найти, например, из уравнения = 1/2:

откуда

и после логарифмирования

Отсюда

Так как натуральный логарифм является функцией возрастающей и , то t₁<t₂.

Г рафики функций p_o(t) и p₁(t) в случае 1 () символически изображены на рис. 3.2.

Рис. 3.2.

Случай 2. В случае 2() асимптоты и совпадают = 1/2. Поэтому графики функций p_o(t) и p₁(t) не пересекаются и имеют общую асимптоту у = 1/2; они изображены на рис. 3.3.

Случай 3. Наконец, в случае 3 ( ) имеем , т.е. асимптота графика функции р₀(t) ле­жит выше асимптоты графика функции p₁(t). По­этому графики функций p_o(t) и p₁(t), не пересекаясь с течением времени , сближаются до определенного предела, ко­торый равен (рис. 3.4).

Рис. 3.4.

Поскольку p₀(t) — вероятность того, что в момент времени t канал свободен, то p₀(t) = р_об(t), где р_об(t) — вероятность того, что заявка, поступившая на вход СМО в момент времени t будет принята к обслуживанию, так как ситуация, когда свободный канал не принимает на обслуживание пришедшую за явку, запрещена. Итак,

.

Одной из часто рассматриваемых характеристик продуктивности СМО является относительная пропускная способность СМО, обозначаемая нами Q(t)¹.

Относительная пропускная способность СМО для момента времени t представляет собой отношение среднего числа обслуженных заявок за единицу времени к среднему числу всех поступивших заявок за то же время, т.е. это есть средняя доля обслуженных заявок среди всех поступивших. Тогда (по опре­делению вероятности):

Таким образом, из равенств (3.9) и (3.10) Q(t) = р_об(t), т.е. относительная пропускная способность СМО в момент време­ни t есть вероятность того, что заявка, поступившая в момент времени t, будет обслужена.

Важнейшей характеристикой эффективности функциониро­вания СМО является абсолютная пропускная способность СМО, обозначаемая A(t)². Абсолютная пропускная способность СМО для момента времени t — среднее число заявок, которое может обслужить СМО за единицу времени.

Из определений Q(t) и A(t) следует с очевидностью, что

Также очевидно, что абсолютная пропускная способность A(t) есть не что иное, как интенсивность v(t) выходящего пото­ка П_вых обслуженных заявок (который, подчеркнем еще раз, не следует путать с потоком обслуживании):

in П_вых = v(t) = A(t)

Поскольку поступившая в СМО заявка получает отказ толь­ко в случае занятости канала, то вероятность отказа р_отк(t) в момент t равна вероятности p₁(t) того, что канал в момент вре­мени t занят:

.

Вероятность отказа p_отк(t) в момент времени t есть не что иное, как средняя доля необслуженных заявок среди всех поступивших для момента t.

Из равенства (3.13), нормировочного условия (3.2) и равенства (3.9) получим, что

P_отк(t) = 1 – p₀(t) = 1 – p_об(t) = 1 – Q(t)

Полезной характеристикой функционирования СМО является среднее время пребывания заявки в системе поступившей в момент t, которое можно определить по формул полного математического ожидания М [Т_сис(t)] непрерывной случайной величины Т_сис(t), представляющей собой время пребывания в системе заявки, поступившей в СМО в момент t.

Можно выдвинуть две несовместные гипотезы Н₀ и Н₁, со стоящие соответственно в том; что в момент t система находилась в состоянии s₀ и в состоянии s₁. Поэтому вероятности этих гипотез р(Н₀) и р(Н₁) равны р(Но) = р₀(t) и р(Н₁) = p₁(t). Если момент t поступления заявки в систему выполняется гипотеза H₀, т.е. канал свободен, то заявка немедленно попадает под обслуживание и условное математическое ожидание М [Т_сис(t) Н₀] величины Т_сис(t) при гипотезе H₀ будет равно среднему времени обслуживания заявки. Если же в момент t поступления заявки выполняется гипотеза Н₁, т.е. канал занят, то заявка получает отказ и М [Т_сис(t) Н₁] = 0. Следовательно, по формул полного математического ожидания (см. [9], с. 77)

откуда, используя то, что , и выражение p₀(t) по формуле (3.8), получим

Среднее время пребывания в системе заявки, поступившей в момент t, совпадает, таким образом (в случае рассматриваемой системы), со средним временем обслуживания заявки, относящимся ко всем заявкам — как обслуженным, так и получившим отказ. А среднее время обслуживания одной заявки представляет собой среднее время пребывания за­явки в системе, относящееся только к обслуженным заявкам.

Из формул (3.9) - (3.11), (3.14), (3.15) видно, что все харак­теристики функционирования СМО выражаются через p₀(t).

Так как процесс, протекающий в СМО, является процессом гибели и размножения, то (см. [5],с. 177) через достаточно дли­тельное время устанавливается предельный (стационарный) режим его протекания, при котором существуют предельные Вероятности состояний, не зависящие ни от времени, ни от начального состояния системы:

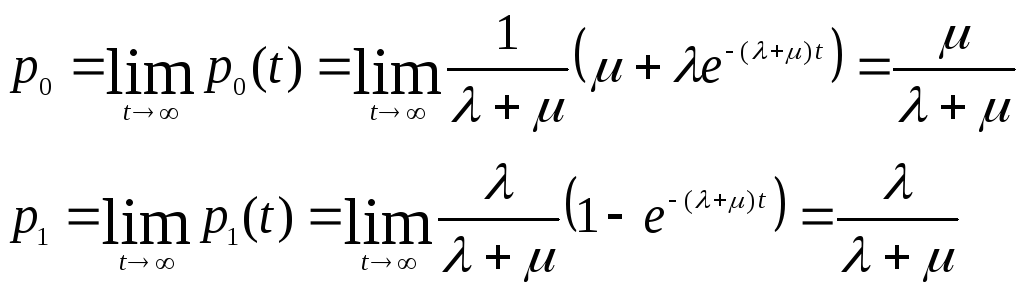
Выражения (3. 17), (3. 18) можно было бы вывести и из об­щих формул предельных вероятностей состояний для процесса гибели и размножения:

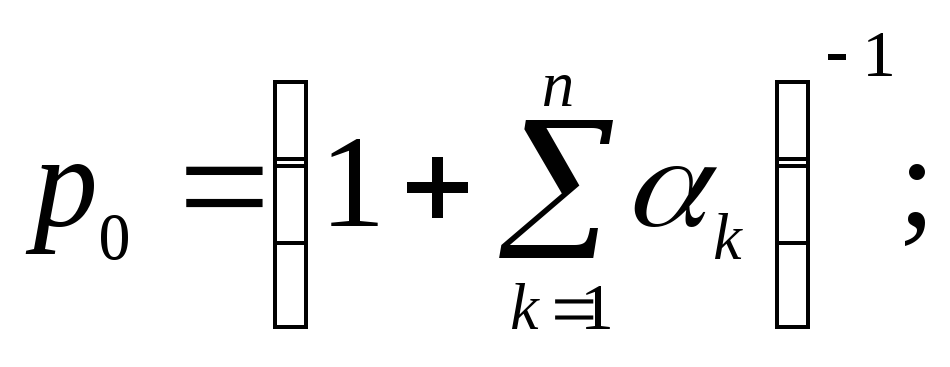
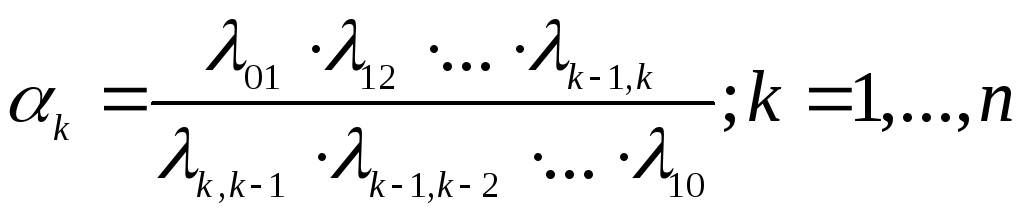
где λ_ij — плотность вероятности перехода системы из i -то со­стояния в j-е (|5],с. 179) при n = 1, λ₀₁ = λ, λ₁₀ = μ.

Предельные вероятности состояний р₀ и р₁ можно выразить через средние времена простоя канала и обслуживания одной заявки . Для этого в формулы (3.17) и (3.18) следует подставить и .

В результате получим:

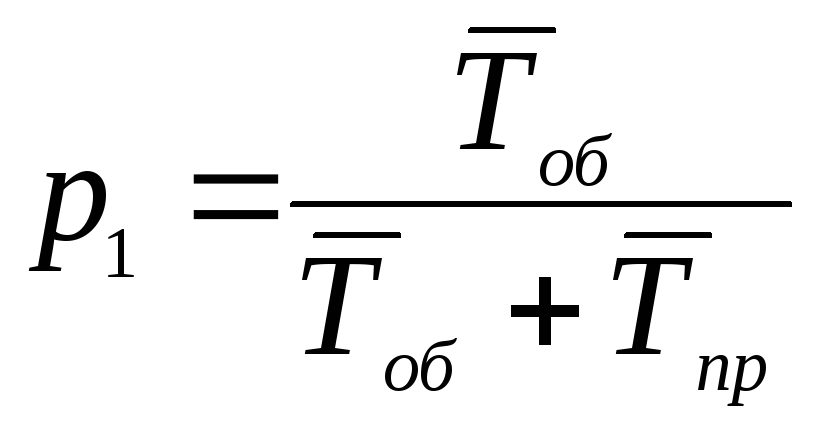
1 in – от англ. Intensity - интенсивность

2 Стационарный пуассоновский поток называется простейшим. Стационарность потока означает, что его вероятностные характеристики не зависят от времени ([5],с. 69)

1 Плотностью вероятности перехода λ_y(t) системы из состояния s_i, я состояние s_j в момент времени tназывается величина

,

где - вероятность того, что система, находившаяся в момент времени t в состоянии s_i, за промежуток времени , (т.е. за время ) перейдет из него в состояние s_j . Полагают, что =0 (см. [5], с. 43). Напомним также, что вероятность р(А) события А есть отношение числа m благоприятствующих событию А элементарных исходов в данном опыте к об­щему числу n исходов: . Таким образом, вероятность любого собы­тия не меньше 0 и не больше 1, т.е. .

2 Размеченным графом состояний системы (в которой протекает случайный про­цесс с дискретными состояниями и непрерывным временем) называется схема, в которой состояния системы обозначаются квадратами (прямоугольниками, кругами), внутри которых помещается обозначение состояния, а стрелками указаны возможные непосредственные переходы из состояния в состояние, при этом у каждой стрелки указывается плотность вероятности перехода (см. [5], с. 7, 27, 44).

1 Случайный процесс, протекающий в системе с n постоянными s₁, … , s_n называется циклическим, если граф состояний этой системы имеет вид:

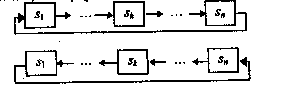
2 Случайный процесс, протекающий в системе с n постоянными s₁, … , s_n называется процессом гибели и размножения, если граф состояний этой системы имеет вид:

1 Колмогоров Андрей Николаевич (25.04.1903 - 20.10.1987) — выдающийся матема­тик, академик, член Академии педагогических наук СССР, профессор Мос­ковского государственного университета, президент Московского математиче­ского общества (1964—1966), иностранный член Парижской академии наук, член Лондонского королевского общества и ряда других зарубежных академий наук. Герой Социалистического Труда, лауреат Ленинской и Государственных премий СССР и международной премии им. Э. Бальзама; основные научные достижения в области теории функций действительного переменного, теории вероятностей, конструктивной логики, топологии, теории дифференциальных уравнений, функционального анализа, приложения математики в механике, военном деле, биологии, технике и лингвистике; заложил основы теории мар­ковских случайных процессов с непрерывным временем.

1 Q – первая буква английского quota – доля, часть, квота.

2 A – первая буква английского absolute – абсолютный.