IT-1_RGR_1

7

Срок сдачи 01.12.15

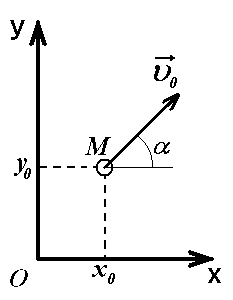Задача 1

Из точки М с координатами и брошено под углом к горизонту с начальной скоростью . Исследовать движение тела в том случае, когда можно пренебречь сопротивлением воздуха и кривизной поверхности Земли. Тело считать материальной точкой. Отсчет времени вести с момента броска тела. Начало декартовой системы координат считать расположенным на поверхности земли. Численные значения начальных параметров движения тела приведены в таблице 1.

Задание 1

Учитывая начальные условия движения тела найдите:

1. зависимость от времени радиус-вектора тела:

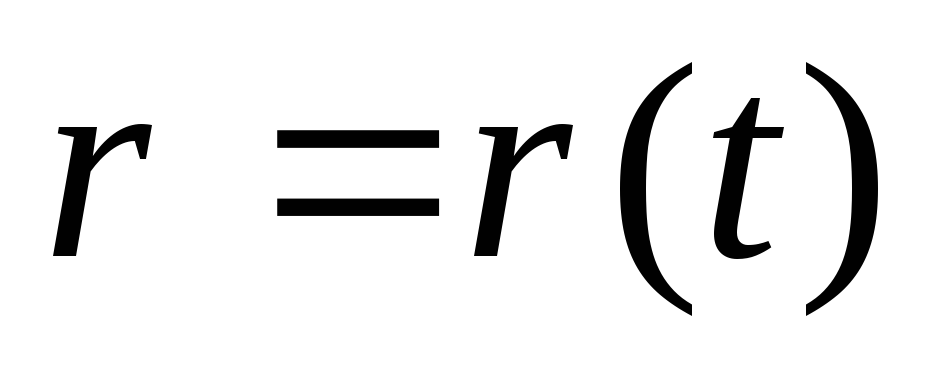
2. зависимости от времени координат тела: ,

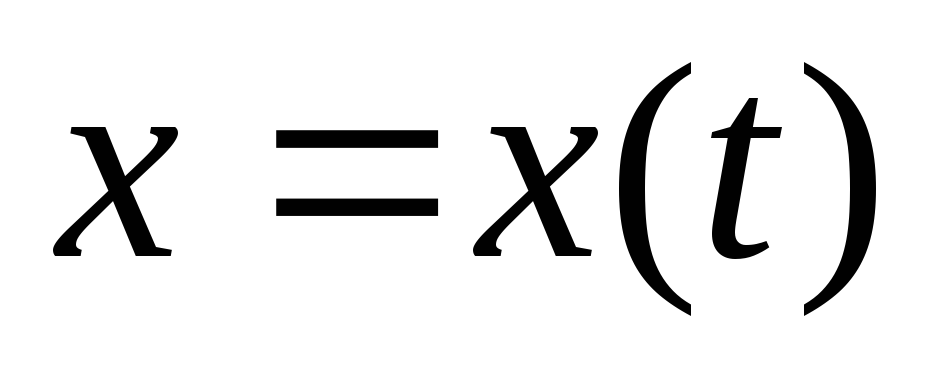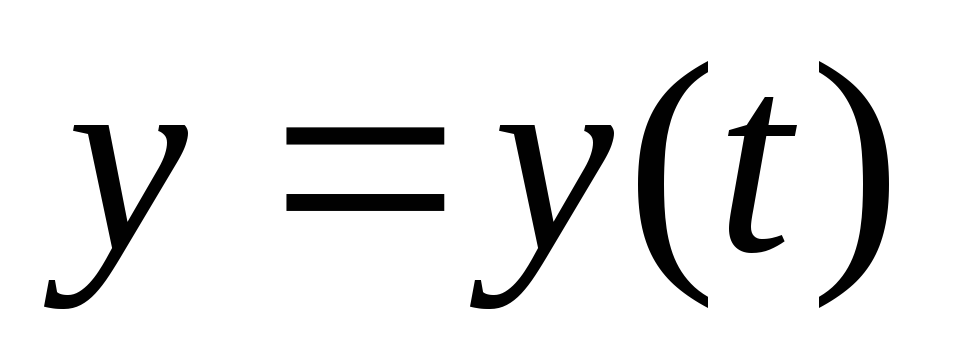
3. уравнение траектории тела:

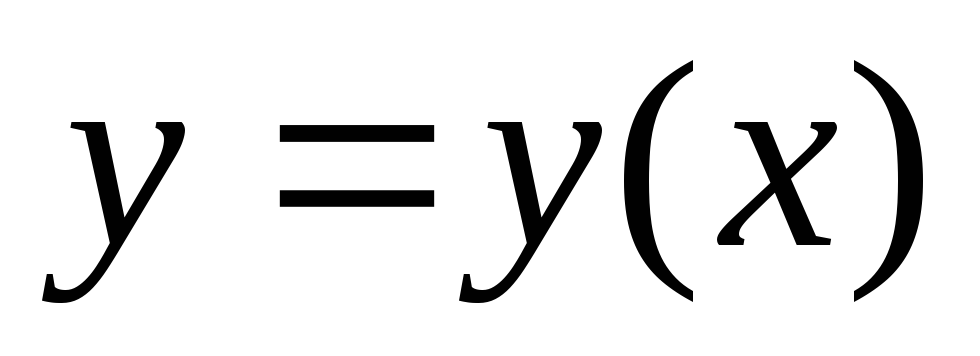
4. зависимости от времени проекций скорости тела: ,

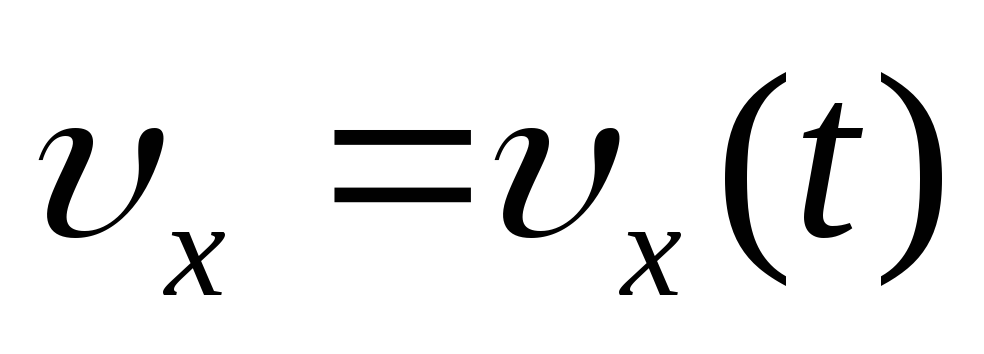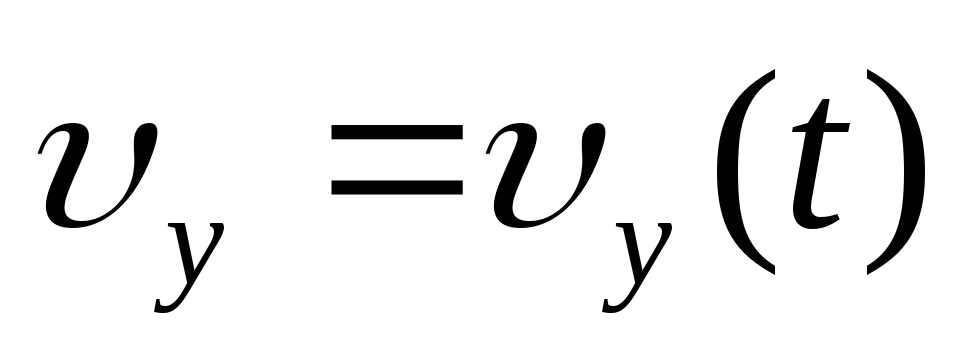
5. зависимость от времени модуля скорости тела:

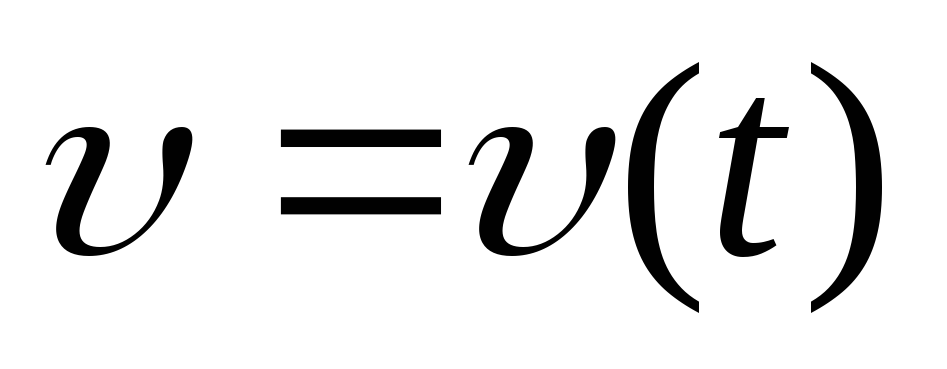
6. зависимость от времени угла между вектором скорости тела и горизонтом

7. зависимости от времени модулей нормального 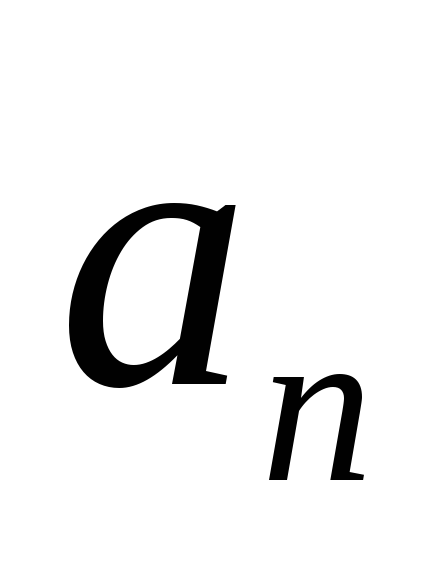и тангенциального ускорений тела

8. зависимость от времени угла между вектором полного ускорения тела и вектором скорости

Задание 2

Найдите численные значения следующих величин:

2.1 продолжительность полета тела , с

2.2 дальность полета тела , м

2.3 модуль полного перемещения тела за время полета , м

2.4 максимальную высоту подъема тела , м

2.5 модуль конечной скорости тела , м/с

2.6 модуль средней скорости за время полета, , м/с

2.7 модули тангенциального ускорения тела в моменты времени =0 и

2.8 модули нормального ускорения тела в моменты времени =0 и

2.9 радиусы кривизны траектории в моменты времени =0 и

Задание 3

Для моментов времени и рассчитайте следующие величины:

3.1 координаты тела , и ,

3.2 модули радиус-векторов и

3.3 модули скоростей и

3.4 модули тангенциальных ускорений и

3.5 модули нормальных ускорений и

3.6 модули полных ускорений и

3.7 радиусы кривизны траектории и

Задание 4

Для промежутков времени , и определите следующие величины:

4.1 проекции модулей перемещений на ось : , ,

4.2 проекции модулей перемещений на ось : , ,

4.3 модули перемещений , ,

4.4 модули средней скорости , ,

Задание 5

Выбрав соответствующие масштабы перемещение и скоростей, изобразите на миллиметровой бумаге формата А4:

5.1 систему отсчета

5.2 траекторию, указав на ней положения тела в моменты времени и

5.3 векторы скорости тела в моменты времени , , и

5.4 векторы нормального и тангенциального ускорений в моменты времени , , и

5.5 вектор полного перемещения тела

Таблица 1

№ варианта	Начальная скорость тела , м/с	Начальные координаты тела		Угол бросания , град	№ варианта	Начальная скорость тела , м/с	Начальные координаты тела		Угол бросания , град
		, м	, м				, м	, м
1	1	1	2	25	16	6	6	3	45
2	2	1	3	30	17	7	5	3	50
3	3	1	4	35	18	8	4	3	55
4	4	1	5	40	19	9	3	3	60
5	5	1	6	45	20	10	2	3	65
6	6	6	1	50	21	1	4	2	70
7	7	5	1	55	22	2	4	4	25
8	8	4	1	60	23	3	4	5	30
9	9	3	1	65	24	4	4	6	35
10	10	2	1	70	25	5	4	7	40
11	1	3	2	20	26	6	6	4	45
12	2	3	3	25	27	7	5	4	50
13	3	3	4	30	28	8	6	2	55
14	4	3	5	35	29	9	6	5	60
15	5	3	6	40	30	10	5	5	65

Задача 2

Диск радиусом вращается из состояния покоя вокруг неподвижной оси согласно уравнению . Направление вращения диска указано на рисунке. Численные значения , , , , и приведены в таблице 2.

Задание 1

Учитывая начальные условия движения тела, найдите: для точек, лежащих на ободе диска, к моменту времени после начала движения:

1. модуль угловой скорости ;

2. модуль линейной скорости ;

3. модуль углового ускорения ;

4. модуль тангенциального ускорения ;

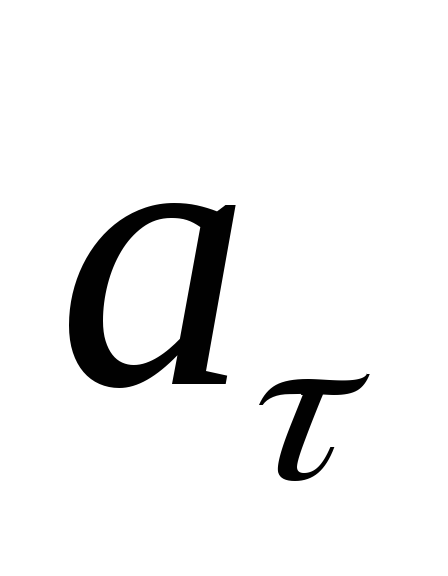5. модуль нормального ускорения ;

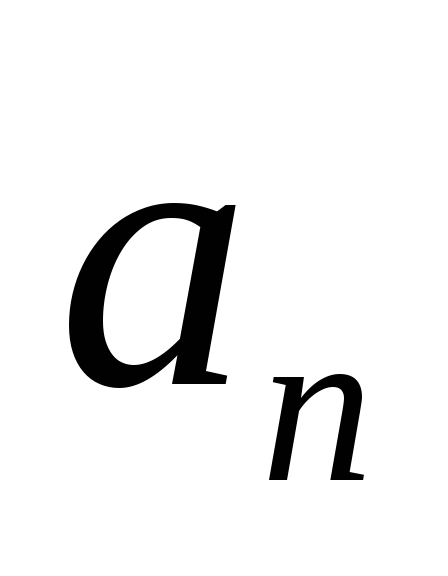6. угол , составляемый вектором полного ускорения с вектором линейной скорости

Задание 2

Выбрав соответствующие масштабы изобразите на миллиметровой бумаге формата А4 взаимное расположение векторов , , и в данный момент времени (рис.1), а также взаимное расположение векторов , и (рис. 2).

Таблица 2

№ вар	, м	, рад	, рад/с	, рад/с2	, рад/с3	, с	№ вар	, м	, рад	, рад/с	, рад/с2	, рад/с3	, с
1	0,1	0	-1	2	1	10	16	0,15	10	0	0,1	0	5
2	0,1	5	1	2	-1	1	17	0,05	2	9	1	-1	2
3	0,05	7	4	0	-0,1	3	18	0,1	3	3	5	-1	1
4	0,2	3	1	2	0	5	19	0,1	4	0	0	0,1	5
5	0,1	0	0	0	1	1	20	0,2	8	34	-1	-0,5	3
6	0,3	8	13	0	-1	2	21	0,2	6	0	1	0,1	5
7	0,1	4	0	1	0	5	22	0,05	4,5	-50	1	1	3
8	0,2	3	6,75	-2,5	1	0,5	23	0,05	7,5	0	0,1	0,5	3
9	0,05	2	0	0	2	1	24	0,1	1	8	0,5	0,5	3
10	0,1	0	5	-0,5	-1	1	25	0,1	0	0	0,5	1	2
11	0,2	0	0	-1	1	2	26	0,15	2	30	-2	-0,5	2
12	0,05	7	0	0,2	2	10	27	0,15	3	0	-1,5	3	1
13	0,15	10	0	-2	4	1	28	0,2	4	5	1	1	1
14	0,1	3	0	0	0,5	2	29	0,2	2	0	10	-2	1
15	0,2	2	0	0,5	0	3	30	0,1	0,1	0,1	1,5	-1	0,5

Задача 3

На вершине клина расположен блок в виде сплошного диска (цилиндра) массой и радиусом . Через блок перекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы массой , и . Коэффициенты трения грузов о плоскость соответственно равны , и . Углы наклона плоскостей клина к горизонту равны и . Получите выражения для определения ускорения тел и сил натяжения нитей. Значения параметров приведены в таблице 3.

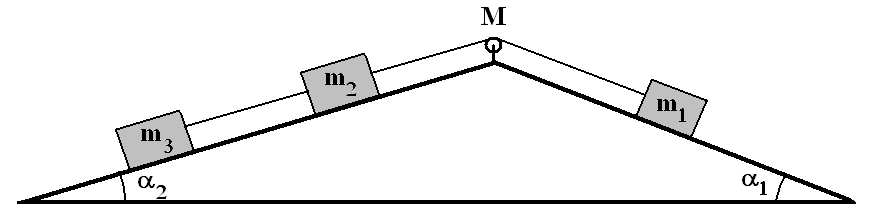
Таблица 3

№ вар.	M	m1	m2	m3	µ1	µ2	µ3	1, град	2, град
1.1	0	m1	m2	m3	0	0	µ3	90	45
1.2	M	m1	m2	m3	0	0	µ3	90	45
2.1	0	m1	m2	0	µ1	µ2	0	45	30
2.2	M	m1	m2	0	µ1	µ2	0	45	30
3.1	0	m1	m2	m3	0	µ2	µ3	90	0
3.2	M	m1	m2	m3	0	µ2	µ3	90	0
4.1	0	m1	m2	m3	0	µ2	0	90	60
4.2	M	m1	m2	m3	0	µ2	0	90	60
5.1	0	m1	m2	m3	µ1	µ2	µ3	60	0
5.2	M	m1	m2	m3	µ1	µ2	µ3	60	0
6.1	0	m1	m2	m3	0	0	µ3	90	60
6.2	M	m1	m2	m3	0	0	µ3	90	60
7.1	0	m1	m2	m3	µ1	µ2	µ3	60	45
7.2	M	m1	m2	m3	µ1	µ2	µ3	60	45
8.1	0	m1	m2	m3	0	µ2	µ3	90	60
8.2	M	m1	m2	m3	0	µ2	µ3	90	60
9.1	0	m1	m2	m3	µ1	µ2	0	45	60
9.2	M	m1	m2	m3	µ1	µ2	0	45	60
10.1	0	m1	m2	m3	0	µ2	0	90	30
10.2	M	m1	m2	m3	0	µ2	0	90	30
11.1	0	m1	m2	m3	µ1	µ2	µ3	60	60
11.2	M	m1	m2	m3	µ1	µ2	µ3	60	60
12.1	0	m1	m2	0	µ1	µ2	0	60	30
12.2	M	m1	m2	0	µ1	µ2	0	60	30
13.1	0	m1	m2	m3	0	µ2	0	90	45
13.2	M	m1	m2	m3	0	µ2	0	90	45
14.1	0	m1	m2	m3	µ1	0	µ3	45	60
14.2	M	m1	m2	m3	µ1	0	µ3	45	60
15.1	0	m1	m2	m3	µ1	µ2	0	60	0
15.2	M	m1	m2	m3	µ1	µ2	0	60	0
16.1	0	m1	m2	m3	µ1	0	µ3	45	0
16.2	M	m1	m2	m3	µ1	0	µ3	45	0
17.1	0	m1	m2	m3	µ1	µ2	µ3	45	30
17.2	M	m1	m2	m3	µ1	µ2	µ3	45	30
18.1	0	m1	m2	m3	µ1	µ2	0	45	0
18.2	M	m1	m2	m3	µ1	µ2	0	45	0
19.1	0	m1	m2	m3	µ1	0	µ3	60	60
19.2	M	m1	m2	m3	µ1	0	µ3	60	60
20.1	0	m1	m2	m3	µ1	µ2	µ3	45	0
20.2	M	m1	m2	m3	µ1	µ2	µ3	45	0
21.1	0	m1	m2	m3	µ1	µ2	0	60	60
21.2	M	m1	m2	m3	µ1	µ2	0	60	60
22.1	0	m1	m2	m3	0	µ2	µ3	90	45
22.2	M	m1	m2	m3	0	µ2	µ3	90	45
23.1	0	m1	m2	m3	µ1	µ2	0	60	30
23.2	M	m1	m2	m3	µ1	µ2	0	60	30
24.1	0	m1	m2	m3	µ1	0	µ3	60	0
24.2	M	m1	m2	m3	µ1	0	µ3	60	0
25.1	0	m1	m2	m3	µ1	µ2	µ3	45	60
25.2	M	m1	m2	m3	µ1	µ2	µ3	45	60
26.1	0	m1	m2	0	µ1	µ2	0	60	45
26.2	M	m1	m2	0	µ1	µ2	0	60	45
27.1	0	m1	m2	m3	0	µ2	µ3	90	30
27.2	M	m1	m2	m3	0	µ2	µ3	90	30
28.1	0	m1	m2	m3	µ1	µ2	0	45	30
28.2	M	m1	m2	m3	µ1	µ2	0	45	30
29.1	0	m1	m2	m3	µ1	µ2	µ3	60	30
29.2	M	m1	m2	m3	µ1	µ2	µ3	60	30
30.1	0	m1	m2	m3	µ1	µ2	0	60	45
30.2	M	m1	m2	m3	µ1	µ2	0	60	45