
lec_opt1
.pdfЗадачи оптимизации |
|
Основные понятия ............................................................................................. |
2 |
....................................................................................................... |
2 |
Процесс оптимизации |
|
Методы одномерной оптимизации ............................. |
3 |
.......................................................................... |
3 |
Аналитический способ нахождения локального минимума |
|
Численные методы.................................................................................................. |
4 |
Методы одномерного поиска .............................. |
6 |
.................................................................................... |
4 |
Методзолотого сечения ........................................................................................ |
5 |
Одномерная оптимизация с использованием производных |
|
Деление пополам...................................................................................................... |
6 |
Метод Ньютона(метод касательной) ............................................................... |
6 |
Безусловная оптимизация ................................................................................ |
12 |
......................................................................................... |
8 |
Квадратичная аппроксимация |
|
Методы прямого поиска .............................................................................. |
17 |
........................................................................................... |
16 |
Метод координатного спуска |
|
Градиентные методы ............................................................................... |
17 |
................................................................................................ |
17 |
Метод наискорейшего спуска |
|
Метод Ньютона..................................................................................................... |
19 |
Задачи оптимизациис ограничениями – разностями (ЗОР) |
|
............................ |
21 |
Метод исключения................................................................................................. |
22 |
Метод множителей Лагранжа. .......................................................................... |
26 |
Нелинейное программирование (НЛП). |
|
................................................................ |
27 |
Методы решения НЛП........................................................................................... |
30 |
Задачи линейного программирования (ЛП)........................................................ |
31 |

Основные понятия
Процесс оптимизации
Имеется задача. Для решения задачи нужно формализовать объект и представить его в виде математической модели.
Модели:
-физические;
-геометрические (фотография, рисунок);
-математические.
Математическая модель, та которая определена с помощью математических формализмов. Математическая модель не является точной, а является идеализацией. Модель характеризуется параметрами, которые могут быть и числовыми р1 , р2 ,K, рп
. Их часть может характеризовать состояние объекта – параметры состояния (р1 , р2 ),
а другие могут относиться к процессу проектирования – переменные проектирования
(рп ).
Определение параметров состояния - задача моделирования. Определение переменных проектирования – задачи проектирования или задачи оптимизации.
Допустим имеются 2 переменные р1 , р2 . Задавая конкретные значения получаем точку.
|
R – множество чисел |
|
R |
G |
множество допустимых |
|
вариантов |
p2 |
допустимое решение |
p1
недопустимое решение – не удовлетворяющее наложенным ограничениям
Плоскость множества возможных вариантов, на нее могут быть наложены ограничения.
Отображение множества F : G → R - целевая функция позволяет формировать критерий для сравнения различных решений.
2вида задач оптимизации:
-максимизации;
-минимизации.
Для оптимизационного решения задачи требуется:
1.Сформулировать задачу;
2.Построить математическую модель (определить множество переменных);
3.Определить ограничения на возможные решения;
4.Определить целевую функцию. Далее применим формальные математические методы, позволяющие найти решения.
2
Методы одномерной оптимизации
Постановка: требуется оптимизировать х (формальная постановка)
|
|
Z = f (x)→opt |
|
|
a ≤ x ≤ b |
f (x) - функция одной переменной a,b, x, f (x) R f (x) - целевая функция.
Решение: найти х, при котором f (x) принимает оптимальное значение.
2варианта:
-минимизировать – задача минимизации;
-максимизировать – задача максимизации.
Рассмотрим случай минимизации
|
|
a,b, x, f (x) R |
Z = f (x)→opt |
||
|
a ≤ x ≤ b |
|
2способа:
-аналитический
-численный
В аналитическом f (x) задается в виде формулы, в численном f (x) задается в виде
черного ящика, на входе подается х, на выходе значение целевой функции в этой точке.
Пусть функция определена в некоторой области S ( x S ), в случае одномерной |
||||||||
оптимизации S – интервал S = {x | a ≤ x ≤ b}: |
|
|
|
|
||||
1. |
точка х* |
называется глобальным минимумом, если для х S, f (x* )≤ f (x) |
|
|||||
2. |
точка |
х* |
называется |
строгим |
глобальным |
минимумом, |
если |
для |
|
х S, f (x* )< f (x) |
|
|
|
|
|
||
3. |
точка х* |
называется локальным минимумом, если для х Ε(x* ), f (x* )≤ f (x) |
||||||
4. |
точка |
х* |
называется |
строгим |
локальным |
минимумом, |
если |
для |
х Ε(x* ), f (x* )< f (x)
Следствие: любая точка глобального минимума является локальным минимумом, обратное не верно.
Аналитический способ нахождения локального минимума f (x) - дифференцируема
f '(x)= 0 - необходимое условие точки локального минимума.
3

f '(x)< 0 |
f '(x)> 0 |
x*
f '(x)= 0
Численные методы
Пусть функция f (x) задана на интервале (a,b), при этом существует такая точка x* , что на [a, x* ]– монотонно убывает, а на [x* ,b]– монотонно возрастает, то функция унимодальная.
а |
x* |
b |
Если из того что |
х1 ≤ х2 следует, что |
f (x1 )≤ f (x2 ), то функция называется |
монотонно возрастающей. Если из того что |
х2 ≤ х1 следует, что f (x2 )≤ f (x1 ), то |
|
функция называется монотонно убывающей.
Методы одномерного поиска
Разобьем [a,b]и вычислим значение функции в каждой точке.
х0 = а х1 х2 |
хn−2 хn−1 b = xn |
|
искомый минимум |
В результате остается интервал меньшего размера, к которому применяется тот же метод, и находим еще один интервал, в конце находим интервал с заведомо нужной точкой.
Интервал неопределенности – интервал, в котором заведомо находится точка минимума. Наиболее эффективное разбиение – двумя точками на 3 равных отрезка.
4

а |
х1 |
х2 |
b |
1)f (x1 )< f (x2 ) (a, x2 )
2)f (x1 )> f (x2 ) (x1 ,b)
2 n - после выполнения n шагов сокращение исходного интервала
3
2 n (b − a)= δ3
δ - точность с которой надо найти решение задачи.
|
2 |
n |
= |
δ |
n ln |
2 |
= ln |
δ |
|
|
|
|
|
|
|
||||
3 |
b − a |
3 |
b − a |
||||||
|
|
|
|
|
N=2n, где n – число шагов, N – число вычислений (мера эффективности данного решения).
Метод золотого сечения
Точки должны быть расположены на равном расстоянии.
|
|
|
|
τ |
|
|
|
|
|
1−τ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
а |
|
|
|
|
|
х1 |
|
|
х2 |
|
b |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
1−τ |
|
|
|
|
|
|
|
τ |
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
τ |
= |
1 −τ |
; |
τ 2 =1 −τ ; τ 2 +τ −1 = 0 ; |
||||||
|
|
1 |
|
|
||||||||
|
|
|
|
τ |
|
|
|
|
|
|||
τ1,2 |
= |
−1 ± |
5 |
τ = |
5 −1 |
≈ 0,618 ; τ - золотое сечение. |
||||||
2 |
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
а
Ε
Εа <1
λ - величина сокращения на каждом шаге
(λ)N = Εa ; N = ln aΕλ
число итераций растет как логарифм функции.
5

Одномерная оптимизация с использованием производных
f (x)→ min . Пусть целевая функция дифференцируема f '(x)= 0 .
точка локального |
точка локального |
точка перегиба |
минимума |
максимума |
|
Методы для нахождения корня уравнения функции 1-ой переменной
Деление пополам
Имеется хотя бы 1 корень. Выбираем любую точку и смотрим какой знак она имеет, такой знак нам и искать. Выбираем точку приблизительно в середине интервала, исследуя значения в 3-х можно отбросить половину интервала.
+
b
а
-
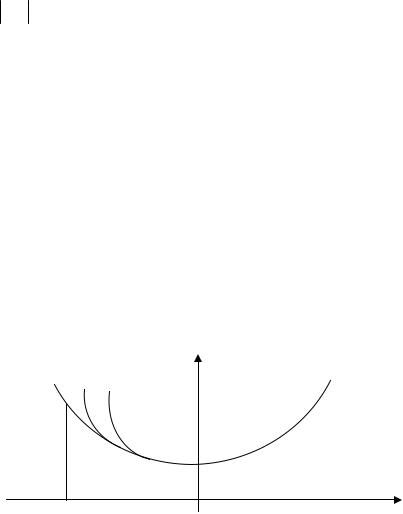
Метод Ньютона (методкасательной)
В случае если известна производная, то выбираем х0 - начальное приближение.
α
х* (х(к+1)) х0 (хк ) х
Допустим, что точка х0 достаточно близка к корню функции и примерно себя ведет линейно не отклоняется. Проведем касательную и находим точку ближе чем х0 , и повторяем до х* .
6
Для метода Ньютона необходимо:
-функция должна иметь производную;
-точка должна быть взята близко к корню;
-функция изменяется близко к линейной функции.
х(к) = х(к+1) − хк ;
f (xк + хк )= f (хк )+ f '(хк ) хк +О(K) - уравнение касательной;
14243
0 |
|
|
|
|
|
h(xк ) |
|||
|
|
х |
к |
= − |
|||||
|
|
|
|
|
|
|
|||
|
|
h'(хк ) . |
|||||||
|
|
|
|
|
|
||||
|
х |
к+1 |
= х |
к |
+ |
х |
к |
||
|
|
|
|
|
|
||||
Если хк < Ε, то вычисления можно прекратить и считать что нужный нам
корень – условие прекращения поиска. (Е – значение корня с некоторой точностью). В методе Ньютона каждя его итерация удваивает количество значащих цифр.
Если все условия выполнены, то эти методы удваивают (ускоряют) количество
значащих цифр: |
h(x)= f '(x); |
|
||||||
|
|
|||||||
|
|
х |
к |
= − |
h(xк ) |
|||
|
|
|
|
|
|
|||
|
|
h'(хк ) |
||||||
|
|
|
|
|
|
|||
|
х |
к+1 |
= х |
к |
+ |
х |
к |
|
|
|
|
|
|
||||
Представим что h(x) линейная функция, то метод Ньютона позволяет найти ее
корень за 1-у итерацию. Целевая функция представляет собой квадратичную зависимость следовательно метод Ньютона позволяет найти минимум или максимум квадратичной функции за 1-у итерацию.
Замена функции на касательную, называется – линейная аппроксимация, и ее применение к целевой функции парабола в точке приближения.
f(x)
xк |
х |
Замена заданной зависимости квадратичной зависимостью, называется – квадратичной аппроксимацией. Метод Ньютона основан на замене заданной зависимости более простой зависимостью.
7

Безусловная оптимизация
Целевая функция зависит от нескольких переменных f(х1, х2, …, хn)→ min. Т.к. нет дополнительных условий накладывающихся на переменные – безусловная оптимизация.
Функции 2-х переменных
f(x1,x2)
x2
x1
Условия определяющие точку минимума – необходимо проанализировать поведение функции в некоторой точке.
х2
х2
Часто под окрестностью подразумевают шар.
Рассмотрим вспомогательное построение:
f (x1 +
линейное векторное пространство
x |
|
, x |
|
+ |
x |
|
)= |
f (x , x |
|
)+ |
|
∂f |
x |
+ |
∂f |
x |
|
|
+O(K) |
2 |
2 |
2 |
2 |
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
1 |
|
∂x1 |
1 |
∂x2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x3
(х1,х2,х3)
x2
x1
8

Скалярное произведение векторов (a,b)= 
 a
a


 b
b
 cos a b , где
cos a b , где 


 - длина вектора
- длина вектора
(норма вектора), a b - угол между векторами.
а S
b

 а
а
 = (а, a)12
= (а, a)12
Допустим, что: a = (a1 , a2 ,K, an ), b = (b1 ,b2 ,K,bn )
n |
|
|
n |
||||||
Тогда: (a,b)= ∑ai bi ; |
|
|
|
а |
|
|
|
= |
∑ai2 |
|
|
|
|
||||||
i=1 |
|
|
i |
||||||
Допустим, что имеется 2 вектора:
(a,b) |
S = ( |
|
, |
|
) |
||||
a |
b |
||||||||
|
b |
|
|
||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
α |
|||||
|
|
|
|
|
|
|
|
(a,b) |
|

 a
a

Чтобы задать направление, мы задаем вектор.
t |
Нормируем вектор |
|
= |
|
|
S |
|
λ |
|
||||||
|
|
|
|
||||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
S
Нормированный вектор имеет тоже самое направление, но 
 λ
λ
 =1, длина.
=1, длина.
Допустим, что задан нормированный вектор 
 λ
λ
 =1.
=1.
|
|
аλ |
аλ = (λ, а)= |
|
|
|
а |
|
|
|
cos a λ |
|
|
|
|
|
|
||||||
|
λ |
|
Скалярное произведение равно 0, |
||||||||
|
|
|
тогда года cos a λ прямой. |
||||||||
|
|
отрицательный |
|
|
|
|
|
|
|
|
|
Возвращаемся к функции 2-х переменных: |
|
|
|
|
|
|
|
|
|
||
9
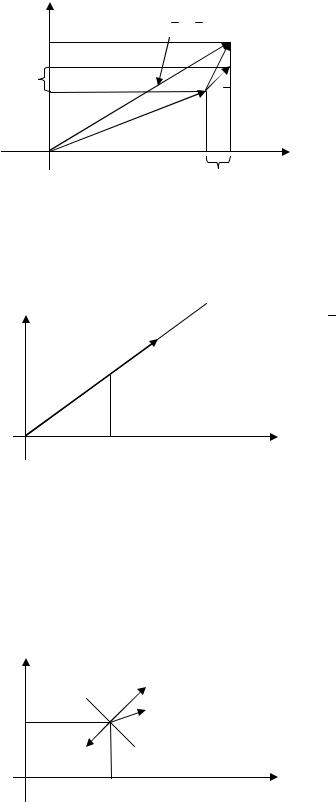
f (x + x |
, x |
+ x |
)= f (x , x |
)+ |
∂f |
x + |
∂f |
x |
+O(K) |
|
∂x |
∂x |
|||||||||
1 2 |
2 |
2 |
1 2 |
|
1 |
2 |
|
|||
|
|
|
|
|
1144242443 |
|
||||
gradf
Отбрасываем члены О(K), приращение будет более точным.
х2 |
|
|
|
х+ х |
|
|
|
х2 |
х = (х1 , х2 ) |
||
х |
х = ( |
х1 , |
х2 ) |
х1 |
х1 |
|
|
|
|
|
|
|
∂f |
|
∂f |
|
|
f (x + |
|
; |
|
|
|||
∂x |
∂x |
|
||||
Вектор gradf = |
|
|
||||
|
1 |
|
|
2 |
|
|
λ
х2  х
х
х1
x)= f (x)+(gradf , x)+O(K) - формула Тейлора.

 λ
λ
 =1
=1
Мы рассматриваем как изменяется точка вдоль данного направления. Функция становится функцией одной переменной.
х- скалярная величина.
f (x + x)= f (x)+(gradf , x)+O(K)
∂∂fx = (gradf , x) - производная по направлению (вдоль данного направления)
max ∂∂fx - направление ряда равное направлению grad (≤ 0).
grad – вектор, в сторону которого функция изменяется более быстро. Антиградиент – grad направленный в другую сторону (-grad).
х2
f(x) |
grad f |
|
|
Необходимое условие: |
|
||
х2 |
gradf = 0 - |
локальный минимум (или |
|
-grad f |
максимум). |
Точки |
локального |
экстремума. |
|
||
х1 |
х1 |
|
|
10
