
lec_opt1
.pdf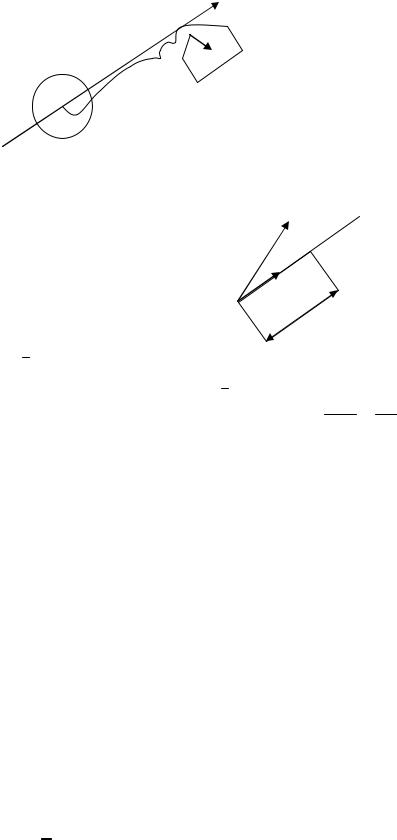
|
|
|
|
|
|
хк - приближение |
в точке |
локального |
||
|
L |
|
S |
x* |
|
минимума, чтобы приблизиться к искомой |
||||
|
|
xK |
|
|
|
точкехк . |
Мы |
должны |
выбрать |
|
|
|
|
|
|
|
направление, в конце получим локальную |
||||
|
|
|
|
|
|
линию. |
|
|
|
|
Допустим, |
требуется |
f(x)Æmin; |
x0 - начальное |
приближение; xK - |
текущее |
|||||
приближение |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x K +1 |
x* |
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
x K |
n |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S K |
|
|
|

 n
n
 =1
=1
а) выбор направления (gradf , n) < 0 ;
б) движение вдоль выбранного направления X K +1 = X K + S K * nK
Задачи оптимизации с ограничениями – разностями (ЗОР)
f (x1 , x2 ,...., xn ) → min |
||||||
g1 (x1 , x2 ,...., xn ) = 0 |
||||||
................................ |
||||||
|
|
|
|
|
|
|
g |
m |
(x , x |
2 |
,...., x |
n |
) = 0 |
|
1 |
|
|
|||
Пример:
f (x) → min g(x) = 0
f |
(x |
, x |
|
, x |
|
x |
|
) → min |
Функции заданы аналитическим выражением |
q1 |
||||||
|
|
1 |
|
2 |
|
|
3, |
|
4 |
|
|
|
можно разрешить относительно |
одной из |
переменных |
|
g1 (x1 , x2 , x3, x4 ) = 0 |
x1 = h1 (x2 , x3 , x4 ) x1 можно |
исключить |
из f |
и q2 , |
||||||||||||
g |
|
(x , x |
, x |
|
x |
|
) = 0 |
|||||||||
|
m |
|
1 |
|
2 |
|
|
3, |
|
|
4 |
|
подставив вместо нее L1 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, x3, x4 ) |
||||
|
|
|
|||||||
f (x2 |
|||||||||
|
|
|
|
, x |
|
x |
|
) = 0 |
|
|
|
|
|
||||||
g(x |
2 |
3, |
4 |
||||||
|
|
|
|
||||||
Тогда, f (x3 , x4 ) x2 x1
x2 = h2 (x3 , x4 )
-задача безусловной оптимизации. Находим x3 , x4 вычисляем
21
Метод исключения
Численное решение:
f (x1 , x2 ) → min
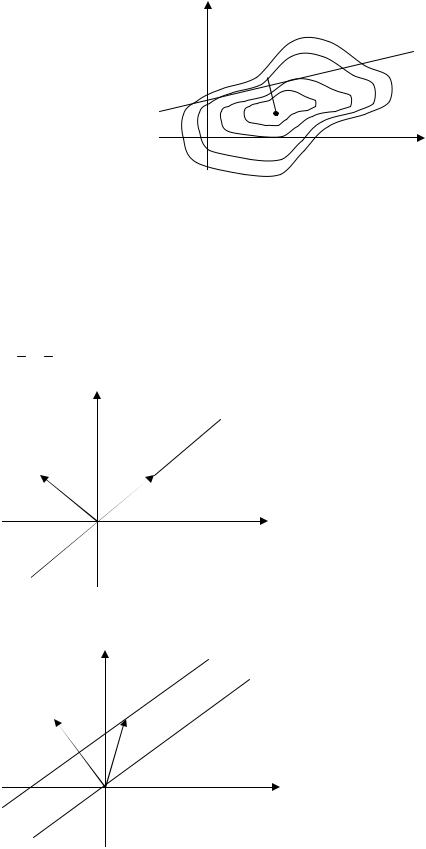
a1 x1 + a2 x2 = b
[g(x1 , x2 ) = a1 x1 + a2 x2 −b] точка min должна лежать на прямой.
x2
g(x)
x1
В каждый момент линия уровня будет касаться прямой эта точка и является точкой
условного локального min. Если в окрестности заданной точки, удовлетворяющей всем значениям равенства, значение функции больше, чем в точке, то эта точка – есть точка условного локального min.
Пример:
a1 x1 + a2 x2 = 0
(a,x)=0 a x
x2
a |
|
x |
x1
Если (a1x)=b
x2
a |
x0 |
x − x0 |
x1
22
Допустим, b = (a1 x0 )
(a, x) −(a, x0 ) = 0 (a, x − x0 )
Прямая будет проходить через некоторую точку удовлетворяющую условию и a Для n переменных f (x) → min , Ax=b
Рассмотрим i-ое ограничение:
ai1 x1 + ai2 x2 +... + ain xn = 0 , (a, x) = 0
a - задан → x - все вектора, лежащие a . Они и составляют гиперплоскость.
При добавлении еще одного условия, уменьшаются размерности. В конечном итоге получится пространство n-m.
|
Для двух переменных возможно 2 случая: |
1. |
2. |
В случае 2 это не точка минимума, а седловая точка.
Рассмотрим точку 3-х переменных:
x3
|
Ограничение – плоскость, следовательно, все |
|
− gradf |
допустимые точки на плоскости. |
|
Если угол grad не равен 90 градусам следовательно |
||
плоскость |
||
|
можно двигаться дальше. На плоскости существует |
|
|
направление, которое будет составлять острый угол |
|
|
с – grad, и двигаясь в этом направлении можно |
|
|
уменьшить значение f. |
|
x |
Если -grad f перпендикулярен плоскости эта точка |
|
2 |
может быть точкой минимума. |
x1
Пусть существует 2 ограничения:
|
|
f (x)→ min |
|
|
||||
|
|
+ a12 x2 +K+ a1n = b1 |
||||||
a11 x1 |
||||||||
a |
x |
+ a |
22 |
x |
2 |
+K+ a |
2n |
= b |
|
21 1 |
|
|
|
2 |
|||
|
|
|
|
|
23 |
|
|
|
Рассмотрим опять случай 3-х переменных:
Точка минимума должна принадлежать пересечению плоскостей. Необходимое условие – вектор антиградиента должен составлять угол 90 градусов с прямой пересечения плоскостей.
Для п-мерного случая имеется п переменных следовательно рассматривая каждое ограничение, получаем п-1 гиперплоскость следовательно рассмотрев т ограничений получим п-т гиперплоскость (т<п).
a11 x1 + a12 x2 +K+ a1n = b1 |
Ax = b |
|||||||||
a |
x |
+ a |
|
x |
|
+K+ a |
|
= b |
|
|
|
21 1 |
|
22 |
|
2 |
M |
2n |
|
2 |
все ограничения |
|
|
|
|
|
|
|
|
|
независимы |
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
+ am2 x2 |
+K+ amn = bm |
|
|||||||
am1 x1 |
|
|||||||||
Т.о. вектора a1 , a2 ,K, am
могут быть выбраны в качестве базиса ортогонального дополнения следовательно градиент принадлежит ортогональному дополнению:
− gradf = λ1 a1 + λ2 a2 +K+ λm am
т.е. линейная комбинация базисных векторов.
v
V = λ1 a1 + λ2 a2
a1 
a2
24
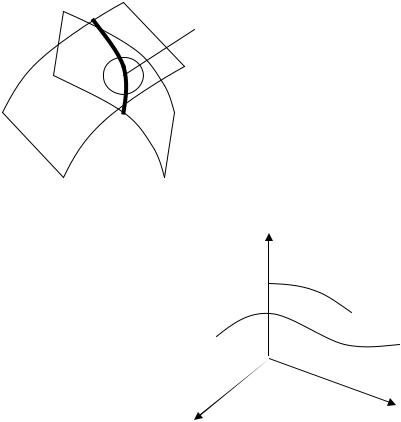
λ1 + λ2 +K+ λm - множители Лагранжа. Рассмотрим матрицу АТ , в ней а1 ,K, аm - столбцы.
− gradf = AT λ
это условие может быть использовано для численного решения задачи оптимизации с ограничивающими уравнениями.
f (x)→ min |
|
Пример: |
Ax = b |
|
|
Ax = b
AT λ = −gradf
Если найдем такие вектора х и λ , для которых эти условия выполняются то точка может быть точкой локального минимума.
Рассмотрим случай когда система ограничений – равенств нелинейная:
f (x1 |
,K, xn )→ min |
|
|
|
|
|
|
||||||
|
g |
|
(x ,K, x |
|
|
)= 0 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
f (x)→ min |
||||||||||
|
|
|
|
M |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)= 0 |
g(x)= 0 |
|||||||
|
g |
m |
(x ,K, x |
n |
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
||
Если функции дифференцируемы, то в окрестности точки минимума они будут вести себя как линейные.
|
|
|
|
* |
|
|
|
|
* |
|
∂gi |
|
|
|
x K |
|
gi (x |
+ x) |
= gi (x |
)+ |
x +O(K) |
|
|||||||
|
|
|
∂x j |
|
||||||||||
|
следовательно в |
окрестности |
точки |
|||||||||||
|
локального |
минимума |
эта |
зависимость |
||||||||||
|
линейная |
следовательно |
получается |
|||||||||||
|
система вида: |
|
|
|
|
|
|
|||||||
|
|
А х = gi (x* )− |
|
(x* + x)+ O(K), |
где |
|||||||||
|
|
gi |
||||||||||||
А = ∂gi
∂x j
следовательно необходимое условие локального минимума: xn
n-m
x1 |
x2 |
− gradf = λ1 gradg1 + λ2 gradg2 +K+ λm gradgm
25

λ1 + λ2 +K+ λm - множители Лагранжа.
f (x)→ min
g(x)= 0
− gradf = λ1 gradg 1 + λ2 gradg 2 +K + λm gradg m
х* - точка может быть искомой в задаче
λ1 + λ2 +K+ λm - множители Лагранжа.
− gradf = λ gradg1 |
+ λ2 gradg2 |
+K+ λm gradgm |
|
n |
14444444244444443 |
||
|
|
m |
|
m |
|
g(x)= 0 |
|
|
|
|
|
Обозначения для скалярного произведения (x, y)= xT y ;
|
|
|
|
|
y1 |
|
( |
|
, |
|
)= (x1 |
,K, xn ) M |
= ∑xi yi ; |
x |
y |
|||||
|
|
|
|
|
|
i |
|
|
|
|
|
yn |
|
L(x, y )= f (x )+ λT g (x )= f (x )+ λ1 g1 (x )+ K + λm g m (x )
Необходимое условие точки локального минимума исходное задание с ограничениями представляет собой необходимое условие точки локального экстремума для функции Лагранжа.
∂L |
=K= f (x)+ λ g |
(x)+K+ λ |
|
g |
|
(x)= |
∂f |
+ λ ∂g1 +K+ λ |
∂gm = 0 |
∂x j |
|
|
∂x j |
||||||
1 1 |
|
m |
|
m |
|
1 ∂x j |
m ∂x j |
∂∂L = gi (x)= 0,i =1,K, m x j
Метод множителей Лагранжа.
Применяется для нахождения точки локального минимума для точек исходной задачи h(x, λ)= f (x)+ λT g(x). Экстремальными точками локального минимума являются седловые.
Пример:
Найти расстояние от точки до прямой в 3-х мерном пространстве.
Плоскость : а11 x1 + a12 x2 +K+ a1n = b1
a21 x1 + a22 x2 +K+ a2n = b2
 y
y
26
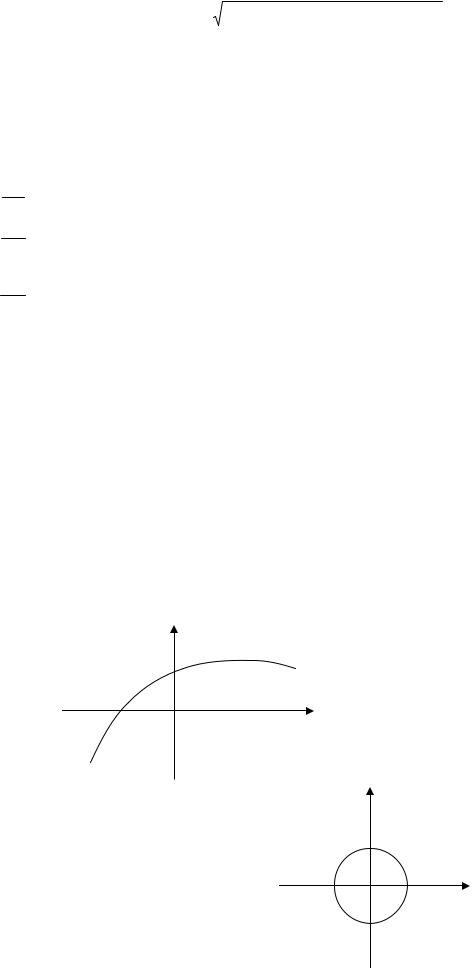
Пересечение плоскостей – линия d = |
(x |
− y )2 |
+ (x |
2 |
− y |
2 |
)2 |
+(x |
3 |
− y |
3 |
)2 |
→ min |
|
1 |
1 |
|
|
|
|
|
|
|
Z = (x1 − y1 )2 + (x2 − y2 )2 + (x3 − y3 )2 → min
а11 x1 + a12 x2 +K+ a1n −b1 = 0 a21 x1 + a22 x2 +K+ a2n −b2 = 0
L(x1 , x2 , x3 , λ1 , λ2 )= ∑j3=1 (x j − y j )2 +λ ∑j3=1 a1 j x j −b1 + λ2 ∑j3=1 a2 j x j −b2
∂L∂x∂ 1
L
∂x2∂LM
∂λ2
= 0 |
|
= 0 |
5 условий дают систему линейных уравнений |
|
|
= 0 |
|
Нелинейное программирование (НЛП).
|
|
|
|
|
|
|
|
|
f (x1 ,K, xn )→ min |
||||||||||||||
|
|
|
|
|
|
|
g |
(x ,K, x |
n |
)= 0,i =1,K, m |
|||||||||||||
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hк (x1 |
,K, xn )≥ 0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
f , gi , hк - заданные функции нелинейные |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
f ( |
|
|
|
)→ min |
||||||||||
|
|
|
|
|
|
|
|
|
x |
||||||||||||||
|
|
|
|
|
|
|
|
|
НЛП |
|
|
|
|
( |
|
|
|
)= 0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
g |
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
)≥ 0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
h |
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим g(x1 , x2 )≥ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x1, x2 ) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 |
+ x2 |
≤ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
2 |
)= 4 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x , x |
2 |
− x2 |
≥ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1
27
В случае системы неравенств пересечение всех областей. Если g > 0, то ограничение неравенства – неактивно (точку можно смещать).
Если точка точно на границе, то говорят, что ограничение активно.
Рассмотрим случай:
аТ х = а х + а |
2 |
х |
2 |
≥ 0 |
|
|
|
|
|
|
|||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если задано |
линейное ограничивающее |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неравенство, |
то вектор |
|
направлен |
||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
внутрь допустимой области. Если аТ х ≤ 0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, то вектор |
а |
будет направлен из |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
допустимой области. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
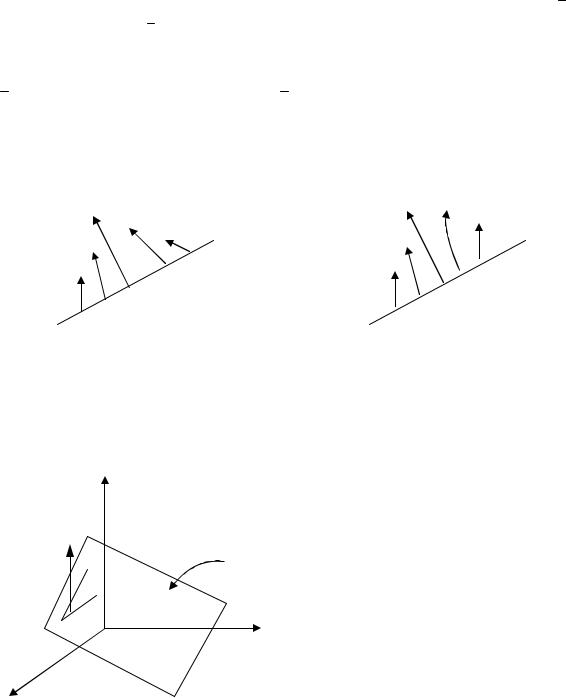
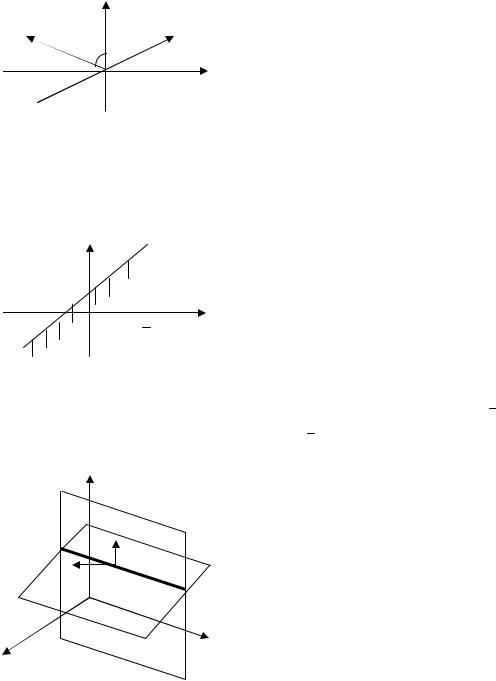
Если аТ х ≥ b , то граница проходит не через начало координат. Необходимые условия:
f (x1 , x2 )→ min a1 x1 + a2 x2 ≥ b
 a
a
1.Если локальный минимум внутри допустимой области, то gradf = 0 ;
2.Если точка локального минимума точно на границе, то gradf = λa , точка является точкой локального, если gradf = λa и λ ≥ 0
|
|
a1 |
|
|
|
|
|
|||
|
|
|
|
|
, |
|
- |
вектора |
нормали |
к |
|
|
|
а1 |
а2 |
||||||
a2 |
|
|||||||||
|
соответствующей плоскости. |
|
||||||||
λ1 , λ2 ≥ 0
В общем случае:
28
f ( |
|
)→ min |
|||||||
x |
|||||||||
|
g1 |
( |
|
|
)= 0 |
||||
x |
|||||||||
|
|
|
|
|
|
M |
|||
|
|
|
|
|
|
|
|
|
|
gm (x)= 0 |
|||||||||
|
h1 |
( |
|
|
)≥ 0 |
||||
|
x |
||||||||
|
|
|
|
|
|
M |
|||
|
h ( |
|
)≥ 0 |
||||||
m |
|||||||||
|
m |
|
|
|
|
|
|
|
|
а) gradf (x)= h1 gradg1 (x)+K+ hm gradgm (x)+ λ1 gradh1 (x)+K+ λp gradhp (x);
λ1 ≥ 0
б) λ2 M≥ 0 ;
λp ≥ 0
в) Если hк = 0 , то λк > 0 . Если hк ≥ 0 , то λк = 0 . Т.е. λк + hк = 0, к =1,K, р. Условие дополняющей нежесткости.
Все 3 условия в совокупности называются условиями Куна-Таккера (условия оптимальности первого порядка).
f (x)→ min
g(x)= 0h(x)≥ 0
Можно записать и так:
f ( |
|
|
)→ min |
|||
x |
||||||
|
|
( |
|
)= 0 |
||
g |
x |
|||||
|
|
|
х ≥ 0 |
|||
|
|
|
|
|
|
|
Ограничения неравенства
ti = hi (x)≥ 0
ti − hi (x)= 0,ti ≥ 0
Поскольку постановка задачи h(x)≥ 0
Основные результаты:
Область п-мерного пространства называется выпуклой если вместе с 2-ми точками, она содержит весь отрезок, соединяющий эти 2 точки.
29
Пример:
Функция нескольких переменных f (x) называется выпуклой если ее матрица Гесса положительно определена.
|
∂2 f |
|
|
|
Т |
|
H = |
|
|
; |
х |
|
Нх ≥ 0 |
|
|
|||||
|
|
|
|
|
|
|
|
∂xi ∂x j |
|
|
|
|
|
Если мы рассматриваем неравенство |
|
f (x)≤ C , то данное неравенство |
||||
определяет выпуклую область.
область будет выпуклой
Th: Пусть дана задача НЛП, если целевая функция этой задачи – выпуклая, и область целевых решений так же выпукла, то локальный оптимум совпадает с ее глобальным оптимумом задачи (задачи выпуклого программирования).
1случай – когда все ограничительные неравенства являются не активными.
2случай – когда точка лежит на границе.
|
|
|
Методы решения НЛП |
|
|
|||
Нулевого порядка – |
Первого |
порядка |
– |
Второго |
порядка. |
|||
поисковые |
методы |
аналогичны градиентным |
Ньютоновские |
методы. |
||||
(безусловные |
методам. |
Условно |
Они |
являются |
||||
ориентиры |
похожи на |
градиентные |
методы. |
специальными |
|
|||
это). |
Используется |
Используется |
и |
Z и |
вариантами |
методов |
||
только |
|
значение |
вектор |
градиента |
(grad |
Ньютона |
для |
|
целевой функции (Z). |
Z). |
|
|
|
оптимизации. |
|
||
|
|
|
|
|
|
|
Используется Z, grad Z и |
|
|
|
|
|
|
|
|
матрица Гесса (Н) |
|
(*) |
|
|
(**) |
|
|
|
(***) |
xK +1 |
|
|
|
|
|
|
|
|
|
xK
(**)
1случай – вектор grad направлен по нормали;
2случай – идет под углом (надо спроецировать поверхность следовательно она будет показывать направление)
Если мы внутри, двигаемся как в (*), а далее (**). Это более эффективный метод.
30
