1.3. Удар

а) классическая теория удара

Интересные превращения кинетической энергии в потенциальную и обратно наблюдаются при ударе тел. Ударом называется кратковременное взаимодействие тел, при этом оба тела деформируются и возникают ударные силы значительной величины. Процесс соударения можно разделить на две фазы:

1. Сближение тел - возникновение деформаций.

2. Разлет - исчезновение деформаций (полное или частичное).

Различают два предельных случая: абсолютно упругий и абсолютно неупругий удары.

При абсолютно упругом ударе на первой фазе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации, на второй фазе тела снова приобретают первоначальную форму, отталкивая друг друга. В итоге потенциальная энергия упругой деформации опять переходит в кинетическую и тела разлетаются. При абсолютно упругом ударе механическая энергия тел не переходит в другие немеханические виды энергии.

Рассмотрим абсолютно упругий удар двух шаров, центры которых движутся вдоль одной прямой. При этом движение вправо будет соответствовать положительной скорости, движение влево - отрицательной.

При абсолютно упругом ударе не выделяется теплота, следовательно систему из двух взаимодействующих шаров можно считать замкнутой (консервативной). К такой системе можно применить закон сохранения импульса и энергии.

Обозначим массы шаров m₁ и m₂ , их скорости до удара и , а после удара и (рис. 1).

Рис. 1. Удар шаров: а) положение до удара; б) положение после удара

Применяем к двум взаимодействующим шарам законы сохранения энергии и импульса:

                                              (1.8)

                                                (1.9)

Перенося слагаемые, содержащие m₁ в одну, а m₂ в другую сторону равенства, получим:

                                               (1.10)

                                                 (1.11)

Деление равенства (1.10) на (1.11) дает:

.                                                        (1.12)

Решая совместно уравнения (1.11) и (1.12), находим значения скоростей U₁ и U₂:

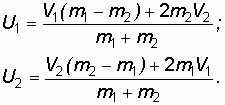                                             (1.13)

По этим формулам определяются скорости шаров после удара. Следует помнить, что в формулах (1.13) скорости U₁ и U₂ могут иметь как одинаковые, так и противоположные знаки, в зависимости от направления векторов и . Проведем анализ полученных результатов по формулам (1.12) и (1.13).

1, Преобразуем равенство (1.12)

  или   .                            (1.14)

В левой части равенства (1.14) - есть относительная скорость шаров до удара, в правой - относительная скорость шаров после удара.

Вывод: относительная скорость шаров после удара остается по абсолютной величине равной относительной скорости шаров до удара, но меняет знак на противоположный.

2. Положим , тогда из первого равенства (1.13) следует, что и из второго равенства (1.13) следует .

Вывод: при упругом центральном ударе двух шаров одинаковой массы, шары обмениваются скоростями.

3. Пусть и , тогда из равенства (1.13) получим: , а .

Вывод: при ударе шара о массивную стенку его скорость меняется на противоположную, скорость же стенки практически не изменяется.

Абсолютно упругий удар является идеальным случаем. В реальных случаях в зависимости от того, из какого вещества изготовлены шары, большая или меньшая часть механической энергии переходит в тепло.

Абсолютно неупругий удар характеризуется тем, что потенциальная энергия упругой деформации не возникает, кинетическая энергия тел полностью или частично превращается во внутреннюю энергию, после удара сталкивающиеся тела либо покоятся, либо движутся с одинаковой скоростью.

При таком ударе шары деформируются, скорости их выравниваются, суммарная кинетическая энергия шаров после удара уменьшается по сравнению с первоначальной (до удара), так как часть ее перейдет в другие формы энергии - тепловую, энергию пластических деформаций и т.д.

Для этого случая закон сохранения энергии запишется в виде:

.                                        (1,15)

Система из двух шаров в этом случае будет являться диссипативной, так как часть механической энергии теряется, рассеивается и по формуле (1.15) можно определить потерю механической энергии Q, которую называют энергией диссипации. Скорость же шаров после удара можно найти, воспользовавшись законом сохранения импульса:

,

откуда

.                                                     (1.16)

При абсолютно неупругом ударе относительная скорость шаров после удара равна нулю: , так как . При абсолютно упругом ударе она, как известно, равна: . При частично неупругом ударе относительная скорость после удара будет составлять некоторую долю относительной скорости шаров до удара:

,                                                 (1.17)

где - коэффициент восстановления относительной скорости шаров при ударе, характеризующий степень упругости взаимодействующих тел и может принимать значения .

Из формулы (1,17) определяется величина коэффициента восстановления

                   

б) волновая теория удара

Классическая теория удара, основывающаяся главным образом на законах сохранения импульса и энергии, позволяет однозначно определить конечные скорости тел. Так как предполагается, что все элементы каждого тела жестко связаны и будут мгновенно испытывать одинаковые изменения движения, являющиеся результатом удара.

В действительности возмущение, порожденное в точке соударения, распространяется в телах с конечной скоростью, и его отражение от граничных поверхностей вызывает колебания и вибрации в телах. Таким образом, все сечения каждого тела при соударении одновременно не подвергаются одинаковому действию сил. Местные быстро изменяющиеся деформации и механические напряжения, вызванные этим возмущением, не могут быть определены методами классической теории, но могут быть исследованы с помощью рассмотрения волнового явления.

Выводы классической теории удара приводят к серьезным ошибкам, когда значительная часть общей энергии обуславливает вибрацию. Этот эффект зависит от соотношения продолжительности удара и периода колебаний, возникающих в телах.

В основе волновой теории удара лежит классическая теория упругости. Уравнения распространения упругих волн получаются в результате совместного рассмотрения трехмерных соотношений между механическими напряжениями и деформациями, условий совместности и уравнений движения.

Соотношения между механическим напряжением и деформацией для однородной изотропной среды записываются следующим образом:

,                                                 (1.19)

где и - проекции нормальных и касательных напряжений; - относительная деформация растяжения (сжатия); - деформация сдвига;

 

- постоянная Ляме; E и G - модули упругости и сдвига соответственно;

Рис. 2. Проекции напряжений, действующих на элементарный объем

Уравнения движения могут быть получены из условия равновесия проекций напряжений, действующих на элементарный объем, который показан на рис. 2

При отсутствии объемных сил в элементе со сторонами dx, dy, dz

Условие равновесия сил приводит к выражениям:

,                                          (1.20)

где - плотность тела; - проекции перемещения (деформации).

Подстановка (1.19) в (1.20) приводит к уравнению движения в перемещениях:

,                                   (1.21)

где 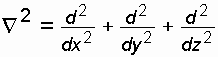- оператор Лапласа.

Решение этих уравнений при заданных начальных и граничных условиях определяет в любой точке тела весь процесс деформирования. С помощью соответствующих преобразований уравнения (1.21) могут быть приведены к виду:

      или                                  (1.22)

где - скорость распространения деформации.

Уравнение (1.22) называется волновым уравнением, указывающим, что  (объемное расширение) распространяется со скоростью волн расширения.

При ударе тел возникает весьма сложное поле напряжений, изменяющихся не только от точки к точке (как при статической нагрузке), но и в данной точке тела со временем. Поле напряжений еще больше усложняется в результате отражения волн от границ тела.

В силу сказанного математическое описание процесса удара в общем виде оказывается настолько сложным, что выходит за рамки возможностей теории упругости. Решение уравнений (1.21) или (1.22) может быть получено лишь для ограниченного числа специальных случаев. В остальных случаях для решения частных прикладных вопросов теории удара приходится применять упрощения и допущения, которые не вели бы одновременно к ошибкам качественного и количественного характера.

Для примера рассмотрим удар двух тонких и длинных стержней с плоскими торцами (рис. 3).

Рис. 3. Удар двух стержней

Для таких стержней все точки, расположенные на поверхности контакта обоих тел, находятся в одинаковых условиях, и, следовательно, скорости и напряжения в них будут одинаковыми.

Это постоянство скоростей и напряжений сохранится для каждого сечения, которого достигнет распространяющаяся волна, расположенного перпендикулярно ее распространению. Пусть ось ОХ направлена вдоль осей стержня. Так как жесткость воздуха ничтожно мала по сравнению с жесткостью стержней и силы трения воздуха о стержень малы, то напряжения на боковые поверхности нормальные к ней , и касательные к ней , . Взаимные касательные напряжения и также равны нулю.

Поскольку диаметр стержней принят малым и стержни однородные, можно полагать, что напряжения в центре сечения мало отличаются от соответствующих напряжений в других точках этого сечения.

С учетом перечисленных условий, можно приближенно считать, что для любой точки соударяющихся стержней справедливы условия , . Таким образом, из рассмотрения исключаются все напряжения, кроме направленного вдоль оси стержней, нормального напряжения .

Напряжения, направленные вдоль оси стержня вызывают кроме продольных  и поперечные деформации и . Эти деформации можно определить по известным в теории упругости уравнениям:

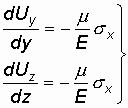,                                                      (1.23)

Решая уравнения (1.23) получим:

; ,

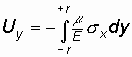где r - радиусы стержней по осям y и z.

Так как  _x не зависит от координат y и z, то

.                                           (1.24)

Если по стержням бежит волна сжатия, то и из равенства (1.24) вытекает, что диаметр стержней увеличивается на величину . В случае волны растяжения, диаметр стержней уменьшается на величину .

Общая система уравнений (1.20) с учетом сделанных допущений значительно упрощается. Второе и третье уравнения тождественно обращаются в нуль, а первое примет вид:

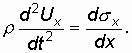
Поскольку , то это уравнение можно переписать в виде:

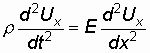 или 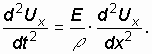                                 (1.25)

Сравнивая (1.25) с (1.22) видим, что волновое уравнение имеет простой вид и легко может быть решено при задании начальных и граничных условий. Коэффициент определяет скорость продольной волны механических напряжений в данном материале.

Простой анализ уравнения (1.25) показывает, что механические напряжения и деформации от поверхности контакта стержней распространяются вдоль стержня со скоростью звука

.