1.5 Передача на местности дирекционных углов линий

Измерить непосредственно на местности дирекционный угол линий не представляется возможным. Для того, чтобы определить дирекционный угол линии, на местности необходимо выполнить определенные построения. Иначе говоря, дирекционный угол можно передать от известного направления другой линии.

Рассмотрим простейший случай. Пусть линия 1-2 имеет дирекционный угол α_1-2 (см. рис. 1.6)

Если линию 1-2 представить в виде вектора, то переход к направлению следующего вектора 2-3 можно выполнить следующим образом. Сначала поменять направление вектора на обратное путём его вращение по часовой стрелке на 180°. Напомним, что вращение по часовой стрелке считается положительным. Затем совершить 2-ой поворот против часовой стрелки на угол βпр, то есть вычесть этот угол. Или иначе:

Рис. 1.6. Схема передачи дирекционного угла

α_2-3 = α_1-2 + 180° - β_пр . (1.4)

В более сложном случае дирекционный угол последовательно передаётся от одной стороны теодолитного хода к другой.

В общем случае можно записать, что дирекционный угол последующей стороны полигона равен дирекционному углу предыдущей плюс 180° и минус угол при вершине лежащей справа по ходу движения.

1.6. Прямая геодезическая задача на плоскости

При производстве съёмочных работ необходимо производить передачу координат от одних пунктов местности к другим. Предположим, что пункт 1 имеет известные плоские прямоугольные координаты x₁ и y₁ (рис. 1.7). Требуется определить координаты пункта 2, то есть x₂ и y₂. Для того, чтобы решить эту задачу необходимо сначала передать дирекционный угол на линию 1-2 и измерить её длину. Линия может иметь наклонное положение, поэтому в конечном итоге требуется знать длину её проекции на горизонтальную плоскость, так называемое «горизонтальное проложение».

Окончательно прямую геодезическую задачу можно сформулировать так. По известным координатам начала линии, её направлению и горизонтальному проложению требуется определить координаты конца линии.

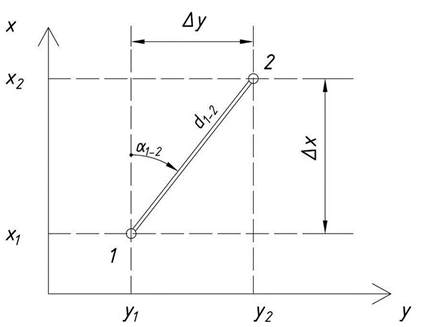
Рис. 1.7 К решению прямой и обратной геодезических задач

Решение задачи может быть проиллюстрировано чертежом (рис. 1.7) и оно состоит из 2 действий.

1). Определяются приращения (разности) координат в виде

Δx=d₁₂ × cos α₁₂ ; (1.5)

Δy=d₁₂ × sin α₁₂ . (1.6)

2). Определяются координаты конца отрезка

x₂=x₁+Δx ; (1.7)

y₂=y₁+Δy . (1.8)

Значения тригонометрических функций вычисляются на инженерных калькуляторах. При этом следует помнить, что прежде, чем использовать функции, значения аргумента, необходимо переформатировать. Минуты с долями переводятся в доли градуса путем деления на 60 и складываются с целыми градусами.

1.7 Обратная геодезическая задача на плоскости

По известным координатам начала и конца линии требуется определить её горизонтальное проложение и направление. Решение задачи осложняется тем обстоятельством, что обратные тригонометрические функции в области определения от 0 до 2π неоднозначны. Исключить неоднозначность можно путём использования понятия румб.

Решение задачи сводится к следующим действиям(см. рис. 1.7):

1. Определяется приращение координат в виде

Δx = x₂ - x₁ ; (1.9)

Δy = y₂ - y₁ . (1.10)

2. Находится модуль румба по одной из зависимостей

│r│=arctg│Δx / Δy│, (1.11)

или │r│=arccos│Δx / d│. (1.12)

При составлении компьютерных программ удобнее пользовать второй зависимостью, поскольку она допускает в вычисленном алгоритме Δx=0.

3. По знакам приращений координат и таблице 1.1 устанавливается четверть, в которой находится направление линии.

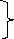
+/- Δx

• четверть

+/- Δy

4. Определяется окончательно румб линии и её дирекционный угол по таблице 1.1.

5. Горизонтальное проложение линии определяется по формуле:

. (1.13)

Решение обратной геодезической задачи целесообразно иллюстрировать схемой для исключения грубых ошибок.