
- •1. Mathcad как инструментальное средство научной работы.
- •2. Приемы работы с системой Mathcad
- •Ввод формул
- •Ввод текста
- •Форматирование формул и текста
- •Работа с матрицами
- •Стандартные и пользовательские функции
- •Решение уравнений и систем
- •Построение графиков
- •Аналитические вычисления
- •Практические занятия
- •Упражнение 1. Простые вычисления с использованием программы Mathсad
- •Упражнение 2. Физические вычисления с использованием единиц измерения
- •Упражнение 3. Векторы и матрицы
- •Упражнение 4. Аналитические вычисления
- •Упражнение 5. Анализ результатов испытаний
- •Упражнение 6. Построение графиков
- •Упражнение 7. Построение трехмерных графиков
- •Упражнение 8. Решение дифференциальных уравнений

Основы Mathcad
4. Дайте команду Insert.Graph.Surface Plot (Вставка.График.Поверхность)
или воспользуйтесь кнопкой Surface Plot (Поверхность) на панели инструментов Graph (График).
5.В появившейся области графика вместо заполнителя укажите имена отображаемых матриц через запятую, заключив все их в скобки: (X0,Y0,Z0).
6.Чтобы изменить формат построенного графика, дважды щелкните на его области. Откроется диалоговое окно 3-D Plot Format (Формат трехмерного графика).
7.На вкладке General (Общие) установите флажок Equal Scales (Равный масштаб), чтобы обеспечить одинаковый масштаб по осям координат.
8.На вкладке Appearance (Оформление) установите переключатель Fill Surface (Заливка поверхности), чтобы обеспечить заливку построенной поверхности.
9.На вкладке Lighting (Подсветка) включите режим освещения поверхности. Установите флажок Enable Lighting (Включить подсветку), отключите все источники света, кроме первого.
10.На панели Light Direction (Направление света) задайте координаты источника света. Используйте кнопку Применить, чтобы сразу видеть последствия сделанных настроек. По окончании настройки закройте диалоговое окно щелчком на кнопке ОК.
11.Путем протягивания мыши в области графика измените направление осей координат, чтобы изображение было видно наиболее отчетливо.
12.Изменяя значение l, можно увидеть форму электронных облаков для разных орбиталей, в том числе и не встречающихся в природе.
Итог. Мы научились строить трехмерные графики с изображением объемных
поверхностей, заданных параметрически. Это фактически означает умение изображать любые фигуры, которые могут потребоваться в ходе практической работы.
Упражнение 8. Решение дифференциальных уравнений
Задача. Найти функцию y(x), удовлетворяющую дифференциальному уравнению
dy/dx+ y = x cos x и имеющую значение 0 при x = 0.
Анализ. Это простое дифференциальное уравнение допускает точное аналитическое решение. В данном упражнении предполагается использование стандартной функции программы Mathcad, осуществляющей численное решение данного уравнения. Результат вычислений можно после этого сравнить с точным решением.
28 |
каф. МиИТ, 2015 |

Основы Mathcad
Рис. 7. Трехмерное изображение электронной f-орбитали
1.Запустите программу Mathcad.
2.Задайте начальное значение функции как элемент вектора y, размерность которого соответствует числу решаемых уравнений (в данном случае единице):
y0: = 0.
3. Создайте функцию T(x, y), которая вычисляет значение производной при за-
данных значениях независимой переменной и неизвестной функции:
T(x, y): = –y0 + x · cos(x).
4. Определите начальное (точка 0) и конечное значение отрезка интегрирования.
a: = 0, b: = 12 ·p.
5.Укажите число шагов интегрирования.
K: = 20.
6.Вычислите численное решение уравнения при помощи функции r k f i x e d. Z: = r k f i x e d (y, a, b, K, T).
7.Результат вычислений — матрица Z с двумя столбцами, первый из которыхсодержит значения независимой переменной, а второй — соответствующиезначения функции.
8.Постройте график полученного решения.
9.Определите аналитическое решение данного уравнения при тех же начальных условиях.
10.Нанесите аналитическую кривую на тот же график и сравните поведение численного и точного решения.
11.Измените число шагов, на которые делится отрезок интегрирования, и исследуйте, как изменяется результат расчета при уменьшении и увеличении этого параметра.
Усков Ю.И. |
29 |
каф. МиИТ, 2015 |
Основы Mathcad
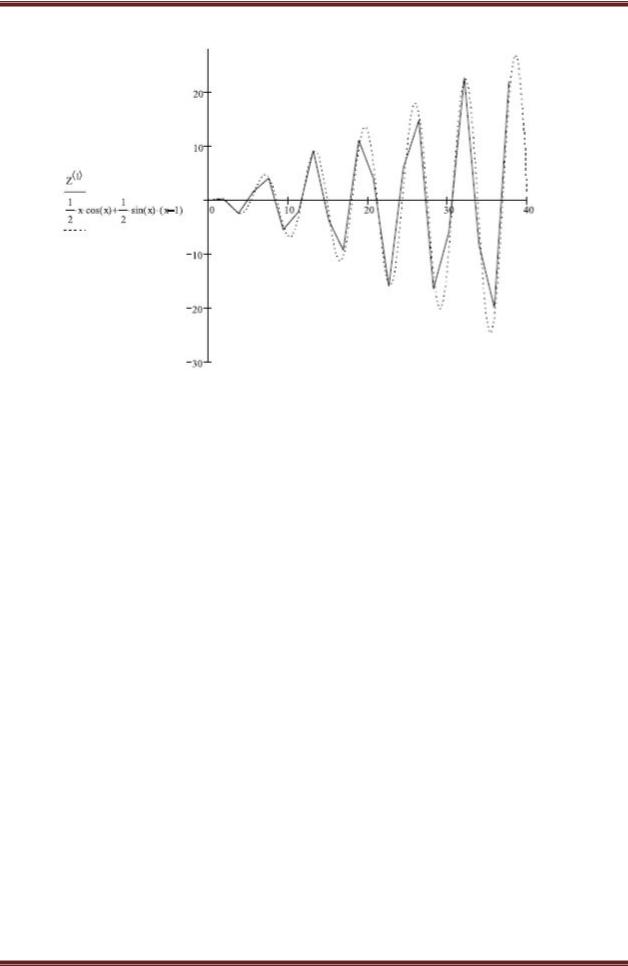
Рис. 8. Графики численного и точного решения дифференциального уравнения
Итог. Мы научились численно решать дифференциальные уравнения первого
порядка с помощью программы Mathcad. Использованный метод без изменений переносится на системы, содержащие два или большее число дифференциальных уравнений. Увеличение величины шага интегрирования ускоряет получение результата, но снижает его точность. При слишком большой величине шага результат расчетов может вообще не соответствовать реальному решению.
Усков Ю.И. |
30 |
каф. МиИТ, 2015 |
