
Глава I.
Системы линейных алгебраических уравнений.
Определение 2.1. Линейным уравнением
с
 неизвестными
неизвестными
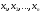 называется
уравнение вида
называется
уравнение вида 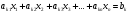 .
.
Здесь коэффициенты
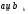 заданные
числа.
заданные
числа.
Определение 2.2. Системой
 линейных уравнений с
линейных уравнений с
 неизвестными
называется выражение вида
неизвестными
называется выражение вида
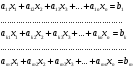 ,
,
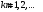 (2.1)
(2.1)
Приведём примеры конкретных систем линейных алгебраических уравнений
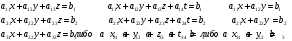 (2.2)
(2.2) 
Чем различаются эти системы. В первой количество уравнений и количество неизвестных совпадают. Во второй количество уравнений меньше количества неизвестных. В третьей количество уравнений больше количества неизвестных.
Определение 2.3.
Если все
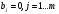 ,
то система называется однородной.
,
то система называется однородной.
Для простоты изложения будем рассматривать системы вида
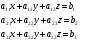 (2.3)
(2.3)
Решением системы (2.3) называется
совокупность трёх чисел
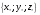 ,
которые после их подстановки в систему
превращают каждое уравнение в тождество.
,
которые после их подстановки в систему
превращают каждое уравнение в тождество.
Определение 2.4. Система называется совместной, если она имеет хотя бы одно решение.
В противном случае система несовместна.
Определение 2.5. Совместная система называется определённой, если она имеет только одно единственное решение. Совместная система называется неопределённой, если она имеет бесконечно много решений .
Определение 2.6. Главной матрицей системы (2.3) называют матрицу
 (2.4)
(2.4)
Матрицы
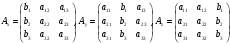
Назовём вспомогательными матрицами системы (2.3)
Матрицу
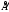 =
=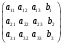 (2.5)
(2.5)
назовём расширенной матрицей системы (2.3)
Теорема Крамера . Если определитель
главной матрицы системы
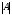
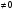 ,
то формулы
,
то формулы
 (2.6)
(2.6)
Дают единственное решение системы(2.3).
Замечание. Если

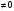 ,
то существует и другой метод решения
системы (2.3).
,
то существует и другой метод решения
системы (2.3).
Матричный метод решения определённых систем уравнений.
1шаг. Записываем систему (2.3) в матричном виде
 (2.7)
(2.7)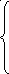
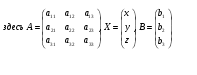
2 шаг. Находим матрицу
 обратную к главной матрице
обратную к главной матрице
 системы.
системы.
3шаг. Умножаем обе части матричной
записи системы
(2.7) на
матрицу
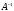 :
:
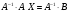
И так как
 получаем решение системы
получаем решение системы
 .
.
Пример 2.1. Решить систему 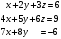
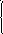
двумя способами: 1) методом Крамера и 2) матричным методом.
-
Решение системы методом Крамера
Так как определитель главной матрицы
системы
 ,
то решать систему методом Крамера
по формулам (3.6) можно.
,
то решать систему методом Крамера
по формулам (3.6) можно.
Находим последовательно
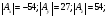
отсюда
Решим эту же систему матричным методом
1 шаг. Записываем систему в матричном
виде
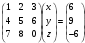
2шаг. Вычисляем
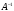 по формуле
по формуле 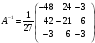
3 шаг. Умножаем обе части системы
слева на обратную матрицу
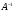

отсюда

Используя результаты занятия 1 (матрицы), рекомендуем читателю все вычисления проделать самостоятельно .
Прежде чем изучать один из наиболее распространённых методов решения систем линейных уравнений, определим понятие равносильных систем уравнений.
Определение 2.7. Две системы линейных уравнений равносильны, если они имеют одни и те же решения.
Теорема 2.1. Если расширенные матрицы двух систем линейных алгебраических уравнений эквивалентны (см. определение 1.12), то системы равносильны.
Приведённый далее метод преобразования одной системы линейных алгебраических уравнений в равносильную ей систему называется методом Гаусса.
