
Глава I.
Матрицы. Основные определения и правила действия.
Определение
1.1. Матрица
это прямоугольная таблица элементов,
имеющая
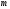 строк
и
строк
и
 столбцов
столбцов
 (1.1)
(1.1)
Матрица
(1.1) называется прямоугольной матрицей
размером
 .
Каждый элемент матрицы нумеруется двумя
индексами. Первый индекс
.
Каждый элемент матрицы нумеруется двумя
индексами. Первый индекс
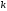 обозначает
номер строки. Второй индекс
обозначает
номер строки. Второй индекс
 обозначает
номер столбца.
Матрица, состоящая из одной строки,
называется вектор - строкой. Матрица,
состоящая из одного столбца, называется
вектор – столбцом.
обозначает
номер столбца.
Матрица, состоящая из одной строки,
называется вектор - строкой. Матрица,
состоящая из одного столбца, называется
вектор – столбцом.
Если число
строк равно числу столбцов ,
то такую матрицу называют квадратной
матрицей размером
,
то такую матрицу называют квадратной
матрицей размером
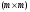 .
.
Пример
1.1. Матрица размером
 имеет
2 строки и 3 столбца
имеет
2 строки и 3 столбца 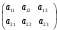
Матрица
размером (3 2)
имеет 3 строки и 2 столбца
2)
имеет 3 строки и 2 столбца
 .
.
Пример
1.2. Элемент
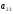 расположен
на пересечении второй строки и третьего
столбца. Элемент
расположен
на пересечении второй строки и третьего
столбца. Элемент
 расположен
на пересечении третьей строки и второго
столбца. Элемент
расположен
на пересечении третьей строки и второго
столбца. Элемент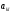 расположен на пересечении
расположен на пересечении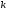 -ой
строки и
-ой
строки и
 -го
столбца.
-го
столбца.
Определение
1.2. Матрицы обозначаются заглавными
буквами. Например, матрица
 ,
матрица
,
матрица
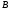 .
Две
.
Две
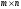 -
матрицы
-
матрицы
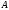 и
и
 равны,
если соответствующие элементы матриц
равны. То есть
равны,
если соответствующие элементы матриц
равны. То есть
 для всех
для всех .
Между матрицами
разных размеров равенства быть не может.
.
Между матрицами
разных размеров равенства быть не может.
Элементы алгебры матриц.
Суммой
двух матриц
А и В одинакового
размера
 называется
называется
 -матрица
, элементами которой являются суммы
соответствующих элементов матриц А и
В. Таким образом С=А+В если
-матрица
, элементами которой являются суммы
соответствующих элементов матриц А и
В. Таким образом С=А+В если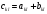 для всех
для всех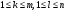 .
.
Пример
1.3. Вычислить
сумму матриц

Решение.
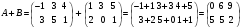 ;
;
Замечание. Матрицы разных размеров складывать нельзя.
Определение
1.3. Чтобы
умножить число
 на
матрицу
на
матрицу
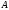 нужно
каждый элемент
матрицы
нужно
каждый элемент
матрицы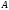 умножить
на число
умножить
на число
 .
.
Определение
1.4. Выражение
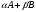 ,
где
,
где
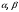 -числа,
а
-числа,
а
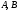 - матрицы называют линейной комбинацией
матриц
- матрицы называют линейной комбинацией
матриц
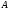 и
и
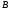 .
.
Правило
1. Умножение вектор
 строки
на вектор – столбец.
строки
на вектор – столбец.
Чтобы перемножить вектор- строку на вектор-столбец с одинаковым числом элементов нужно перемножить первый элемент строки на первый элемент столбца, второй элемент строки на второй элемент столбца ит.д. и затем полученные произведения сложить.
Пример
1.4. Пусть
заданы:
вектор- строка
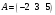 и вектор-
столбец
и вектор-
столбец требуется
перемножить А на
В.
требуется
перемножить А на
В.
РЕШЕНИЕ.
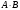 =
=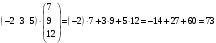 .
.
Правило
2. Умножение матрицы А размером
(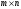 ) на матрицу В размером (
) на матрицу В размером (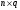 ).
).
При умножении
матрицы А размером
 на матрицу В размером
на матрицу В размером
 получается
матрица С размером
получается
матрица С размером
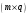 .
Причем элемент
.
Причем элемент
 матрицы С получается перемножением
матрицы С получается перемножением
 ой
строки А матрицы и
ой
строки А матрицы и
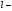 го
столбца В матрицы.
го
столбца В матрицы.
Замечание. Правило 2 говорит нам о том, что если число столбцов первого сомножителя совпадает с числом строк второго сомножителя, то такие матрицы перемножать можно .
Пример 1.5. Перемножить матрицы А и В
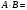
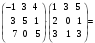
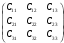
РЕШЕНИЕ.
Условия перемножения матриц выполнены.
Начнём с вычисления элемента
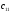 .
Нужно первую строку А матрицы умножить
на первый столбец В матрицы:
.
Нужно первую строку А матрицы умножить
на первый столбец В матрицы:
 =
=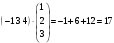 .
Чтобы вычислить элемент
.
Чтобы вычислить элемент
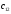 нужно
первую строку А матрицы умножить на
второй столбец В матрицы:
нужно
первую строку А матрицы умножить на
второй столбец В матрицы: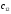 =
= .
.
Чтобы
вычислить элемент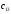 нужно первую строку А матрицы
умножить на третий столбец
нужно первую строку А матрицы
умножить на третий столбец
матрицы В
матрицы:
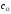 =
= .
.
Остальные элементы С матрицы находим аналогично. Рекомендуем читателю самостоятельно их вычислить.
Ответ: 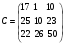 .
.
Пример 1.6.
Умножение столбца на строку. Перемножить .
.
Решение.
Выписываем правило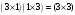 .
В результате должна получиться матрица
.
В результате должна получиться матрица

С размером
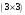 (сравните
с результатом умножения строки на
столбец ( см. пример 1.4))
(сравните
с результатом умножения строки на
столбец ( см. пример 1.4))
Ответ: 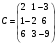 .
.
Пример
1.6. Умножение матрицы на столбец.
Перемножить
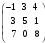
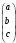
Решение.
Выписываем правило
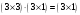 .
Перемножать можно. В результате
получается матрица-столбец размером
.
Перемножать можно. В результате
получается матрица-столбец размером
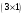 .
Выписываем ответ
.
Выписываем ответ
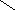

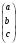 =
=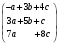
Квадратные матрицы.
Матрица, у которой число строк совпадает с числом столбцов ,называется
квадратной
матрицей. Матрицу размером
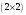 называют матрицей 2-го порядка.
называют матрицей 2-го порядка.
Матрицу
размером
 называют
матрицей 3-го порядка и так далее.
называют
матрицей 3-го порядка и так далее.
Определители квадратных матриц.
Определение
1.5. Определитель матрицы обозначается
обозначается
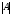 или
или
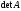 .
.
Определение 1.6. Определитель третьего порядка вычисляется разложением по первой строке по формуле
 (1.2)
(1.2)
Определение 1.7. Определитель 2-го порядка также вычисляется разложением по первой строке по формуле
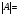
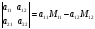 (1.3)
(1.3)
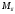 -называется
минором элемента
-называется
минором элемента
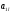 .
Минор
.
Минор
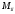 -
это определитель, который получается
из определителя
-
это определитель, который получается
из определителя
 вычёркиванием первой строки и
вычёркиванием первой строки и
 го
столбца.
го
столбца.
Определение
1.8. Минор элемента
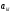 -
это определитель, который получается
из заданного определителя вычёркиванием
-
это определитель, который получается
из заданного определителя вычёркиванием

 ой
строки и
ой
строки и
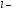 го
столбца.
го
столбца.
Пример 1.7. Выписать миноры всех элементов определителя 3-го порядка и вычислить определитель

Решение.
Вычисляем
миноры элементов первой строки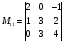
 .
.
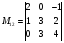
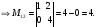
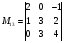
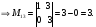
О стальные миноры определителя вычисляются аналогично (проделайте это)
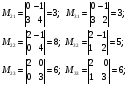
Вычисляем
определитель по формуле (1.2) 
Замечание. Определители любого порядка большего, чем третий также можно вычислять
разложением по первой строке по правилу

Здесь
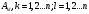 -это
алгебраические дополнения .Вычисляемые
по формуле
-это
алгебраические дополнения .Вычисляемые
по формуле .
.
Единичные матрицы
Определение 1.9. Матрицы вида
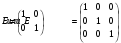
называются единичными матрицами второго и третьего порядков соответственно.
Замечание.
 .
Матрица не изменится , если её умножить
на единичную
.
Матрица не изменится , если её умножить
на единичную
матрицу (проверьте).
Обратные матрицы
Определение
1.10. Матрица
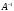 называется
матрицей обратной к матрице
называется
матрицей обратной к матрице
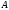 если
если
