
Лекция 7
.pdfУСТОЙЧИВОСТЬ ЯВНОЙ РАЗНОСТНОЙ СХЕМЫ
Исследуем гармонику umj j ei m , ( ) - амплитуда, - фаза
Решение будет устойчиво, если числа лежат внутри круга |
||||||||
единичного радиуса: |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
Подставив гармонику в волновое уравнение, получим: |
||||||||
2 |
|
|
2 |
2 |
2 |
|
0 |
|
|
|
|
|
|
sin |
|
|
|
2 1 2r g |
|
1 |
||||||
|
|
|
|
|
|
|
2 |
|
По теореме Виета произведение корней уравнения равно 1.
Для того, чтобы модули чисел 1,2 были меньше 1, они должны быть комплексно сопряженными, т.е. дискриминант уравнения
2 |
2 |
2 |
|
2 |
2 |
|
2 |
|
|
|
|
|
|
D 4r g |
sin |
|
|
r g |
|
sin |
|
|
|
0. |
|
|
|
|
2 |
|
2 |
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Неравенство выполняется для всех , если |
K g |
|
1 |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
K - число Куранта
НЕЯВНАЯ РАЗНОСТНАЯ СХЕМА
uij 1 2uij uij 1 |
gi |
j 12 |
uij 11 2uij 1 uij 11 |
|
2 |
j 1 |
|
|
|
|
|
|
fi |
||
|
|
|
|
|
|
||
2 |
|
|
|
h2 |
|
|
|
Неявная схема безусловно устойчива, т.е. обеспечивает сходимость разностной задачи к решению соответствующей дифференциальной при любом отношении /h.
Решение на первых двух временных слоях определяется из начальных данных так же, как это сделано для явной схемы.
Обозначив gij 12r2 , перепишем схему в виде
uij 11 (1 2 )uij 1 uij 11 2uij uij 1 2 fi j 1, i 1, 2, ..., N 1.
Дополнив схему формулами, аппроксимирующими краевые условия, получим СЛАУ с трехдиагональной матрицей, которая решается с помощью метода прогонки
СТАНДАРТНЫЕ ФУНКЦИИ MATHCAD
Используется блок Given – Pdesolve
Необходимо уравнение записать в виде системы, введя функцию v(t) = u (t):
Given
u |
(x,t) v(x,t) |
|
v (x,t) g 2 |
u |
xx |
(x,t), |
||||||||||
|
t |
|
|
|
x |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v(x,0) 0 |
|
|
|
|
|
|
|||||
u(x,0) sin |
|
|
|
|
|
|
|
|||||||||
u(0,t) 0 |
|
L |
|
|
v(0,t) 0 |
|
|
|
||||||||
u(L,t) 0 |
|
|
|
|||||||||||||
|
u |
|
|
|
u |
|
|
0 |
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
: Pdesolve |
|
, x, |
|
,t, |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
v |
|
L |
T |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(Подробнее см справку MathCAD)
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
u |
2u |
|
2u |
F (x, y), |
(x, y) G R2 |
|
x2 |
|
y2 |
|
|
2D уравнение Пуассона
Описывает распределение электростатического поля и стационарное распределение температуры
В одномерном случае уравнение Пуассона - краевая задача первого рода для ОДУ второго порядка
Необходимо задать граничные условия на границе G
u(x, y) G = γ
Краевые условия первого, второго и третьего рода
Частный случай: уравнение Лапласа u 0
МЕТОД УСТАНОВЛЕНИЯ
Уравнение Пуассона является стационарным вариантом уравнения теплопроводности
На этом основан Метод установления. В правую часть
u
уравнения Пуассона добавляют слагаемое t и решают 2D
уравнение теплопроводности до тех пор, пока решение не перестанет изменяться в зависимости от времени
Решение нестационарной задачи стремится к решению стационарной независимо от выбора начальных данных
Время в этой задаче является фиктивным, и в разностных схемах надо использовать максимально возможный шаг
При использовании явных схем процесс установления занимает продолжительное время
Применение схем дробных шагов существенно сокращает время решения
ИТЕРАЦИОННЫЕ МЕТОДЫ
Не связаны со сведением к уравнению теплопроводности
Приводят к решению СЛАУ с заполненной матрицей, которая решается итерационным методом
Лежат в основе стандартных функций пакета MathCAD
Область решения - прямоугольник G a x b, c y d
Краевые условия первого рода: |
u(x, y) G = γ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
h |
|
|
b a |
|
hy |
d c |
|
|||
Прямоугольная расчетная сетка с шагами |
x |
|
|
|
|
|
||||||||||
|
||||||||||||||||
|
|
|
|
N x , |
|
|
N y . |
|||||||||
|
u j |
2u j |
u j |
|
u j 1 |
2u j |
u j 1 |
F j |
||||||||
|
i 1 |
|
i |
i 1 |
|
|
|
i |
|
|
|
i |
i |
|||
Конечно-разностная схема: |
|
hx2 |
|
|
|
|
|
|
|
hy2 |
|
|
|
i , |
||
i 1, ...,Nx 1, j 1, ...,Ny 1, |
|
|
|
|
|
|
|
|
|
|||||||
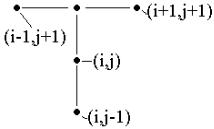
Граничные условия u0j 1j , uNj x |
2j , ui0 |
3i |
, uiN y |
4i . |
||||||||||||
|
|
|
|
|
|
РЕАЛИЗАЦИЯ СХЕМЫ |
|
|
|
|||||||
Приведем к общему знаменателю: |
|
u j 1 h2 h2 F j |
|
|||||||||||||
|
h2 |
u j |
2u j u j |
h2 |
u j 1 |
2u j |
|
|||||||||
|
y |
i 1 |
|
|
i |
i 1 |
|
x |
i |
|
i |
|
i |
y x i |
|
|
Выразим uij через остальные неизвестные: |
|
|
|
|
||||||||||||
|
2 h2 h2 |
u j |
h2u j |
|
h2u j |
h2u j 1 |
h2u j 1 h2h2 F j , |
|
||||||||
|
|
x |
y |
|
i |
y i 1 |
y |
i 1 |
|
x i |
|
x i |
x x i |
|
||
|
|
|
|
ПОТОЧЕЧНЫЙ ИТЕРАЦИОННЫЙ МЕТОД |
|
|
|
|||||||||
2 h2 |
h2 |
u j n 1 |
h2u j n |
|
h2u j n h2u j 1 n |
h2u j 1 n |
h2h2 F j , |
, |
||||||||
x |
y |
i |
|
|
|
y i 1 |
|
y |
i 1 |
|
x i |
|
x i |
|
x x i |
|
где n – номер итерации, i 1, ...,Nx 1, |
j 1, ...,N y 1 |
|
|
|
||||||||||||
Начальное |
приближение |
uij (0) |
задается |
произвольно. |
||||||||||||
Метод сходится медленно. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
БЛОЧНЫЙ МЕТОД ЗЕЙДЕЛЯ |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Векторно-матричная форма: |
Aiui 1 |
Ciui |
Bi ui 1 Fi , |
|
|||||||||||||||||||||
|
|
ui0 |
|
|
0 |
0 ... |
0 |
|
|
|
|
0 |
|
0 |
... |
0 |
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
hy2 ... |
|
|
|
|
|
|
|
|
hx2 |
|
|
|
|
|
|
|
|
|
|
ui |
|
|
0 |
0 |
|
Bi |
0 |
|
... |
0 |
|
|
|
|
|||||||||
ui |
|
... |
|
Ai |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
... ... |
|
|
|
, |
|
|
|
|
... |
... |
|
|
|
|
|
|
||||
|
|
|
N y |
|
|
... |
... |
|
... |
|
... |
|
|
|
|
||||||||||
|
|
ui |
|
|
0 |
0 ... |
0 |
|
|
0 |
|
0 |
... |
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
0 |
|
0 |
... 0 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
hx2 |
2 hx2 hy2 |
hx2 |
... 0 |
|
h2 h2 fi |
|
|
|
|
|
|
|
|
|||||||||||
|
|
F |
|
|
|
|
|
|
|
||||||||||||||||
Ci |
|
|
|
|
|
|
|
|
|
|
i |
|
x |
y |
... |
|
|
j |
|
|
j |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u0 1 , |
uN x |
2 , |
j 1, ...,N y . |
||||||
|
... |
|
|
... |
|
... |
... 0 , |
|
|
|
|
|
|
i |
|||||||||||
|
|
0 |
|
|
0 |
|
0 |
...1 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
n |
|
|
|
|
n |
|
|
i 1, ...,Nx 1. |
|
|
||||||||
Итерации: Aiui 1 |
|
Ciui |
|
Biui 1 |
|
Fi , |
|
|
|||||||||||||||||
Система с блочно-трехдиагональной матрицей
Решается с помощью метода матричной прогонки
Есть много модификаций метода
СТАНДАРТНЫЕ ФУНКЦИИ MATHCAD
Для решения уравнения Пуассона с нулевыми краевыми условиями используют функцию multigrid(F,ncycle)
F – матрица размера (M+1) (M+1), содержащая правую часть уравнения в узлах разностной сетки;
ncycle – параметр численного алгоритма (количество циклов в пределах каждой итерации), можно выбрать равным 2.
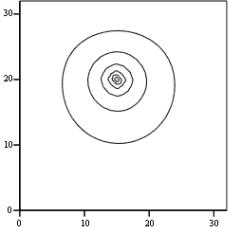
Пример |
решения |
краевой |
M=32 |
||
FM,M =0 |
|||||
задачи для уравнения Пуассона |
|||||
F15,20=104 |
|||||
на сетке из |
33 33 |
узлов. |
G=multigrid(-F,2) |
||
|
|
|
|
||
Функция |
правой |
части |
|
||
F(x,y) = 0 всюду, кроме одной |
|
||||
точки с номером (15, 20), в |
|
||||
которой |
она |
принимает |
|
||
значение 104 |
|
|
|
||
G
СТАНДАРТНЫЕ ФУНКЦИИ MATHCAD
Для решения краевой задачи с ненулевыми краевыми условиями можно использовать встроенную функцию relax(a,b,c,d,e,F,v,r)
a, b, c, d, e – квадратные матрицы коэффициентов разностной схемы:
a uij 1 b uij 1 c uij 1 d uij 1 e uij F,
F – квадратная матрица, задающая правую часть уравнения,
v – квадратная матрица граничных условий и начального приближения к решению
r – параметр, характеризующий скорость сходимости метода, должен лежать на интервале (0,1).
