Файловый архив студентов. Файловый архив студентов.
1260 вузов, 4594 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Новосибирский государственный архитектурно-строительный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Лекция 7

.pdf
Скачиваний:
7
Добавлен:
14.03.2016
Размер:
597.9 Кб
Скачать
☆

УРАВНЕНИЕ С ПЕРЕМЕННЫМ КОЭФФИЦИЕНТОМ

u

C(x,t)

u

0

,

0 x L

,

t 0

t

 

x

 

 

 

устойчивая аппроксимация зависит от знака С(x, t)

гибридная схему Куранта – Изаксона – Риса (КИР):

un 1

un

 

C j

C j

 

 

un un

 

C j

C j

 

 

un

un

 

j

j

 

 

 

 

 

j j 1

 

 

 

 

 

j 1

j 1

0

 

 

 

 

 

 

 

2

 

 

h

2

 

 

 

h

 

 

 

 

 

 

 

 

 

 

симметричная схема

 

un 1

un 1

un un

 

 

 

un 1 un (un 1

un

)

 

 

j

j 1

j

j 1

C

 

j

 

 

j

j 1

j 1

 

 

0

 

 

 

2

 

 

 

 

 

 

 

 

2h

 

 

 

 

схема Лакса

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

un 1

un

 

 

un

un

 

 

h2

 

un

2un un

 

 

 

 

j

j

C j

j 1

 

j 1

 

 

 

 

j 1

j

j 1

0

 

 

2h

 

2

 

h2

 

 

 

 

 

 

 

 

 

 

 

 

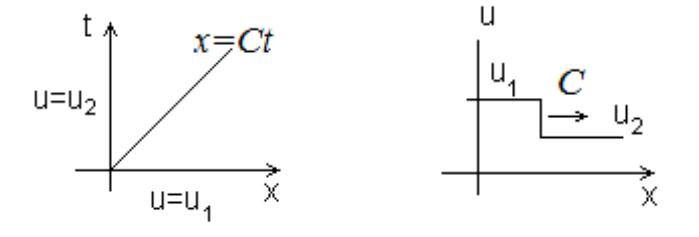
РАЗРЫВНЫЕ РЕШЕНИЯ

Уравнение переноса может иметь разрывные решения.

Разрыв может формироваться в начальный момент из-за несогласованности начальных данных и краевых условий на прилегающей границе Если начальные данные содержат разрыв, то он будет

«переноситься» по характеристике:

а

Будет ли разностная схема сохранять это свойство уравнения?

ПЕРВОЕ ДИФФЕРЕНЦИАЛЬНОЕ ПРИБЛИЖЕНИЕ

Способность разностной схемы воспроизводить разрывные решения называется К-свойством.

Первое Дифференциальное приближение (ПДП)

 

un 1 un

 

un un

 

 

j

j

C

j j 1

0

Явная схема «против потока»

 

h

 

 

Разложим решение в ряд Тейлора в окрестности точки (tn, x ):

 

 

 

 

 

 

 

 

 

 

 

 

 

j

unj 1 unj

ut

 

2

utt ...

 

un

un h u

 

 

h2

u

 

...

2

;

 

 

 

 

 

 

 

j 1

j

x

2

 

xx

 

Подставив эти выражения в схему, получим Г-форму ПДП:

 

 

 

 

 

 

h

 

 

ut

 

 

utt

C ux

 

 

uxx

0

2

2

 

 

 

 

 

 

 

СХЕМНАЯ ВЯЗКОСТЬ

Преобразуем выражение, используя исходное уравнение:

 

u Cu

,

 

u Cu

xt

C(u )

x

C

2u

xx

 

t

 

 

 

x

 

 

tt

 

 

 

 

 

 

t

 

 

 

 

u Cu

 

C2u

 

 

Ch

u

 

 

 

 

 

 

П-форма ПДП:

 

 

 

 

 

 

 

 

 

 

t

x

 

2

 

xx

 

2

 

 

xx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ch C

 

 

 

 

 

 

 

 

 

 

 

 

 

Обозначим

 

 

 

 

 

 

1

. Получили:

ut Cux uxx

 

 

h

 

 

2

 

 

 

 

 

 

В правой части - вторая производная (вязкость, диффузия)

r

C

 

1

, > 0, схема «размазывает» разрывы

 

h

 

 

 

 

 

 

 

 

 

 

r

C

 

1, =0, разрывные решения воспроизводятся точно

 

 

 

 

 

h

 

 

 

 

r

 

C

 

1,

< 0. Задача некорректна. Любое

решение с

 

 

h

 

 

 

 

 

 

 

 

 

начальными данными при t = 0 разрушается за

несколько

 

временных шагов

 

ПДП НЕЯВНОЙ СХЕМЫ

ut Cux

 

Ch

 

C

 

 

1

 

uxx

,

2

 

 

 

 

 

h

При любом числе Куранта в схеме присутствует положительная схемная вязкость

Это обеспечивает абсолютную устойчивость

Однако разрывы всегда «размазываются»

ПРОГРАММА В MathCAD

для явной противопоточной схемы

advec(u0 C L T M N)

h

L

 

 

 

 

 

 

 

 

 

N

 

 

 

 

ta

 

T

 

 

 

 

 

 

 

 

 

M

 

 

 

 

K C tau

 

 

 

 

 

 

 

h

 

 

 

 

for i 0 N

 

 

 

 

xi h i

 

 

 

 

 

 

 

 

ui 0 u0 xi

 

 

 

 

 

 

 

 

 

 

for j 1 M

 

 

 

 

u0 j u0 j 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

for i 1 N

K ui j 1

ui 1 j 1

 

 

ui j

ui j 1

 

 

 

 

 

 

 

 

 

u

 

 

 

Начальные

данные

 

 

 

u0(x)

1

if x 0

 

otherwise

 

0

Задание: исследовать поведение решения при различных значениях K

ВОЛНОВОЕ УРАВНЕНИЕ

utt g2 x,t uxx f x,t

 

 

 

x

 

 

, t

 

 

 

 

Область решения:

G:

 

0, 1

 

0,T

 

.

 

 

 

 

 

 

 

Начальные данные: u(x,0) 1 (x);

 

ut (x,0) 2 (x)

 

p0u (0,t) p1 ux (0,t) A(t)

Краевые условия

s0 u (1, t) s1

ux 1,t B(t)

 

dx

g(x, t)

 

 

 

 

Характеристики:

 

 

 

 

 

dt

 

 

 

 

 

 

 

 

КОНЕЧНО-РАЗНОСТНЫЙ МЕТОД

Построим в области G сетку:

x= ih, t= j , i= 0, 1, ... , N; j= 0, 1, ... , M,

h и — шаги сетки по x и t, соответсвенно.

uij - значение сеточной функции в точке (xi, t j). Используем конечно-разностные соотношения:

2ut 22ux2

( x ,t j )

u( x

i

,t j 1 ) 2u( x

,t j ) u( x

i

,t j 1 )

 

u j 1 2u

j u

j 1

 

 

 

i

 

 

 

 

i

i

i

 

,

 

 

 

 

2

 

 

 

 

 

 

2

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,t j )

u( x

i 1

,t j

) 2u( x

,t j ) u( x

i 1

,t j

)

 

 

u j

2u j

u j

 

 

( x

 

 

i

 

 

 

 

i 1

i

i 1

,

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

h2

 

 

 

 

 

 

 

 

h2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Подставив эти выражения в уравнение, получим явную разностную схему:

u j 1

2u j u j 1

 

u j

2u j u j

i

i

i

(g j )2

i 1

i

i 1

f j

 

 

 

 

 

 

 

2

 

i

 

h2

 

i

 

 

 

 

 

 

ЯВНАЯ КОНЕЧНО-РАЗНОСТНАЯ СХЕМА

Для вычисления значения искомой

(i, j+1)

 

 

 

 

функции на временном слое j+1

(i-1, j)

 

 

 

 

необходимо

знать значения этой

 

 

 

 

 

функции

на

двух

предыдущих

 

 

 

 

(i+1,j)

 

 

 

 

слоях j и j - 1. Решение на

 

 

 

 

 

временном

слое t = t0

определено

 

(i,j-1)

 

 

 

 

 

начальными данными: u i0 1(xi ).

Шаблон явной схемы для

волнового уравнения

Для того, чтобы вычислить решение при t=t1, воспользуемся формулой Тейлора и исходным уравнением:

u(t1 , x) u(t 0 , x) ut (t 0 , x)

2

utt (t 0 ,

2

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

0

 

 

d 2 1 ( x)

1 ( x)

2 ( x)

 

g

 

(t

 

, x)

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

2

 

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

x) 63 uttt (t 0 , x) ...

f (t 0 , x) C 3 .

РЕАЛИЗАЦИЯ ЯВНОЙ СХЕМЫ

Во внутренних узлах i=1,2,…N-1 используем формулы:

u j 1 2u j u j 1 r2 g 2 (u j

2u j u j

) 2 f j ,

r

 

 

 

 

 

h ,

i

i i

i 1

i i 1

i

 

 

 

 

 

 

Для определения решения при x=x0, x=xN, воспользуемся краевыми условиями. В случае первой краевой задачи значения

функции задаются точно: u 0j A(t j ), u Nj B(t j ).

Для второй и третьей краевой задачи производные в краевых условиях заменяем конечно-разностными соотношениями

 

 

 

u j u j

 

 

 

 

 

 

u j

u j

 

p u j p

1

0

A j ,

s u j

s

 

N

N 1

B j ,

 

 

 

 

 

 

 

0 0

 

1

 

 

h

 

 

0

N

1

 

 

h

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

j

 

 

p u j A j h

 

 

j

 

 

B j h s u j

j 2,3,...M .

откуда получим:

u

0

 

1 1

 

,

u

N

 

 

 

1

N 1

,

 

 

 

 

 

 

 

 

 

 

 

p1 p0h

 

 

 

 

hs0

s1

 
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности