
Лекция4
.pdfПриближенное решение ОДУ
ОБОБЩЕНИЕ МЕТОДА ЭЙЛЕРА НА СИСТЕМУ ОДУ
|
dyj |
f |
x, y , y |
,...,y , |
j 1, 2,..., n |
Все условия |
|
|||||||||
|
|
заданы в |
|
|
|
|
||||||||||
|
dx |
j |
1 |
2 |
n |
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
одной точке! |
|||||||||
|
Начальные условия |
|
||||||||||||||
|
y j x0 y j |
|
|
|
|
|
|
|
|
|
||||||
ЗАДАЧА КОШИ ИСПОЛЬЗУЕМ МЕТОД ЭЙЛЕРА |
|
|
|
|||||||||||||
ПРИМЕР: Система 2х ОДУ первого порядка: |
|
|
|
|
|
|||||||||||
y f (x, y, z) |
|
. |
y(a) y0 , |
z(a) z0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
, |
x [a, b]; |
|
|
|
|
|
||||||||
z g(x, y, z) |
|
|
|
yi 1 |
yi |
f (x , y |
|
|
|
|||||||
Обобщение метода Эйлера: |
, z |
), |
||||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
h |
|
i |
i |
|
i |
|
|||
Реализация: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
zi 1 |
zi |
|
|
|
|
|
|
||||||
|
|
|
|
|
0 |
0 |
g(xi |
, yi |
, zi |
). |
||||||
|
|
|
y0 =y , z0 =z , |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
yi+1=yi+h f(xi , yi ,zi), |
h |
|
|
|
|
zi+1=zi+h g(xi, yi, zi). i=0, 1,..., M-1. |
11 |
|
|
|
|
Приближенное решение ОДУ
ОБОБЩЕНИЕ МЕТОДОВ РУНГЕ-КУТТЫ НА СИСТЕМУ ОДУ
Система 2х ОДУ первого порядка:
y f (x, y, z) |
x [a, b]; |
y(a) y0 , |
z(a) z0 |
|
|
, |
|||
z g(x, y, z) |
|
|
|
|
Обобщение двухэтапного метода Рунге-Кутты:
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
k1 f (xi , yi , zi ), |
l1 g(xi , yi , zi ), |
|
|
|
||||||||||
k2 f (xi h, yi hk1, zi hl1 ), |
|
|
|
|||||||||||
l2 g(xi h, yi hk1, zi |
hl1 ) |
|
|
|
|
|
||||||||
y |
|
y |
|
h |
k1 k2 |
, z |
|
z |
|
h |
l1 l2 |
. |
|
|
i 1 |
i |
|
i 1 |
i |
|
|
||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
12 |
|||
Приближенное решение ОДУ
УРАВНЕНИЕ ВТОРОГО ПОРЯДКА:
y p( t )y q( t )y r( t ), |
t [ a, b ] |
2 дополнительных условия на функцию y заданы в одной точке x=a
|
0 |
|
0 |
- начальные данные |
|
y(a) y , |
y (a) z |
|
|
||
|
|
|
|||
Задача Коши с помощью замены: z(t)=y(t), z(t)=y(t) |
|
||||
|
|
|
. |
|
|
сводится к системе 2х ОДУ первого порядка: |
|
||||
y f (t, y, z) z |
|
|
|
||
|
|
|
|
|
|
z g(t, y, z) p(t)z q(t) y r(t) |
|
||||
y(t), z(t) – искомые функции; |
|
||||
f ( t, y, z ), g (t ,y ,z) –функции правых частей; |
|
||||
y0, z0– начальные данные |
|
13 |
|||
Приближенное решение задачи Коши для ОДУ 1 порядка
•Для решения задачи Коши в MathCAD используется процедура Odesolve
•Член с высшей производной должен быть линейным
•Количество начальных условий должно равняться порядку ОДУ
•Необходимо создать блок решения, который начинается с ключевого слова Given и заканчивается вызовом Odesolve
•Внутри блока задается ОДУ и начальные условия
•Число разбиений можно не задавать, программа сама выберет оптимальное значение
•Для решения используются методы Адамса (многошаговые) или Рунге-Кутты (одношаговые)
•Опции решателя выбираются через контекстное меню

Пример 1 - начало
Дано: |
d y |
- y cos(t) ½ sin 2 t , |
t [0, 3], |
y(0) 0 |
|||
dt |
|||||||
|
|
|
|
|
|
||
|
|
|
|
||||
Точное решение: |
u(t) sin(t) e- sin(t) -1 |
|
|
||||
Проверка точного решения в MathCAD:
u(t) sin(t) e sin(t) 1
d u(t) cos (t) e sin(t)cos (t) dt
Начальные данные u(0) 0 
|
1 |
|
sin(2 t) |
|
|
|
sin(t) |
|
|
u(t)cos (t) |
|
|
sin(2 t) |
|
cos (t) |
|
e |
|
sin(t) 1 |
2 |
2 |
|
|
||||||
|
|
|
|
|
|
|
|||
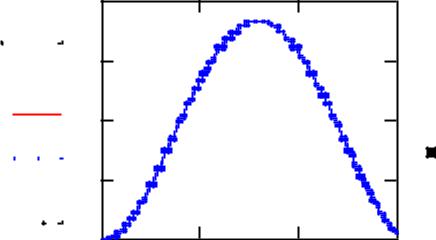
Пример 1 - конец
Решение в MathCAD
Given |
d y(t) |
|
y(t)cos (t) |
1 |
sin(2 t) |
y(0) |
|
0 |
||
|
|
|
|
|||||||
2 |
||||||||||
|
|
|||||||||
|
dt |
|
|
|
|
|
|
|||
y Odesolve(t 3)
0.4 |
|
|
|
|
0.368 |
|
|
|
|
0.3 |
|
|
|
|
u(t) |
|
|
|
|
y(t) 0.2 |
|
|
|
|
0.1 |
|
|
|
|
0 |
|
|
|
|
0 |
0 |
1 |
2 |
3 |
|
0 |
|
t |
3 |
ПРИМЕР 2
Задано уравнение гармонического осциллятора |
|||||
2 |
d 2 y |
|
dy |
y 0 |
|
dt 2 |
dt |
||||
|
|
|
|||
Описывает колебание маятника (угол отклонения от вертикали) с демпфированием. Начальные данные задают начальное значение угла и скорости
|
0, y(0) 1 |
|
y (0) |
||
Параметры 0.5, |
0.2 |
|
задают частоту колебаний и величину демпфирования.
Найти решение задачи Коши с помощью встроенных функций MathCAD
Использование блока Given-Odesolve
Решение с помощью вычислительного блока Given-Odesolve
|
0.5 |
|
0.2 |
|
|
|
|
|
Given |
2 y'' (t) |
y' (t) y (t) |
|
0 |
||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
y' (0) |
|
0 |
y (0) |
|
1.0 |
||
|
|
|
||||||
|
|
|
||||||
y Odesolve(t 10)
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t) |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
|||||||
Сведение к системе ОДУ
|
|
|
|
|
|
y (t) z |
|
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
z (t) |
|
2 ( y y ) |
|||
|
|
|
|
|
|
y(0) 1, |
|
z(0) 0 |
|||
Обозначим: u1=y(t), u2=z(t)

Решение с помощью встроенной функции
rkfixed
ORIGIN 1 |
|
|
|
|
|||
u1 1 |
u2 0 |
t0 0 |
tk |
||||
|
|
|
|
u2 |
|
|
|
|
|
|
|
|
|
|
|
D(t u) |
u1 |
|
u2 |
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
||
U rkfixed u t0 tk n D
10
|
1 |
|
|
|
|
|
|
U 2 |
0 |
|
|
|
|
|
|
U 3 |
1 |
|
|
|
|
|
|
|
2 |
0 |
2 |
4 |
6 |
8 |
10 |
|
|
|
|
U 1 |
|
|
|
