Задание на самостоятельную работу
По изложенной в методических указаниях теме в соответствии с рабочей программой предусмотрена самостоятельная работа. Задание на самостоятельную работу студент получает от преподавателя на занятии. Чтобы выполнить самостоятельную работу необходимо решить следующие задачи по 3: 16.1 – 16.30.
Контрольные вопросы
Дайте определение плоскопараллельному движению. Приведите примеры.
Сформулируйте теорему, в соответствии с которой можно определить скорость любой точки тела при плоскопараллельном движении.
Что такое вращательная скорость токи М вокруг полюса А? Как определить ее модуль и направление?
Сформулируйте следствие из теоремы о проекциях скоростей двух точек тела при плоскопараллельном движении?
Что такое план скоростей?
Что такое мгновенный центр скоростей?
Как можно представить плоскопараллельное движение твердого тела, если известно положение МЦС?
Что надо знать для определения положения мгновенного центра скоростей?
Практическое занятие № 5
Тема: определение ускорений точек тела при плоскопараллельном движении.
Цель: освоить два способа определения ускорений точек тела при плоскопараллельном движении.
Время проведения: 2 часа.
1. Последовательность выполнения
изучить теоретический материал;
ответить на контрольные вопросы;
разобрать предложенные примеры решения задач;
решить самостоятельно предложенные номера задач.
2. Краткие теоретические сведения
2.1. Основные понятия и определения
Определить ускорения точек тела при плоскопараллельном движении можно двумя способами.
Первый способ основан на следующей теореме.
Теорема. Ускорение любой точки тела при плоскопараллельном движении равно геометрической сумме ускорения полюса и ускорения точки в ее вращательном движении вокруг полюса:
,
(4)
где
– нормальное и тангенциальное ускорение
полюса;
–центростремительное
и вращательное ускорение звена АМ.
Перечисленные составляющие ускорения точки М определяются по формулам:
,
(5)
,
(6)
,
(7)
,
(8)
г
Рис.7.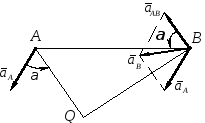
BА, BА – угловая скорость и угловое ускорение звена АМ.
Применение теоремы – см. далее пример.
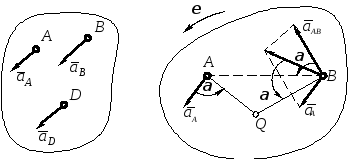
Второй способ определения ускорений точек тела при плоскопараллельном движении основан на понятии и определении положения мгновенного центра ускорений – точки Q (рис. 7). Далее подробно рассмотрено определение положения мгновенного центра ускорений при различных исходных данных задачи.
2.2. Различные случаи определения положения мгновенного центра ускорений.
Все задачи на определение положения мгновенного центра ускорений плоской фигуры можно свести к трем указанным ниже основным случаям, каждому из которых, очевидно, соответствует ряд частных случаев, зависящих от характера движения плоской фигуры.
2
Рис.
8.
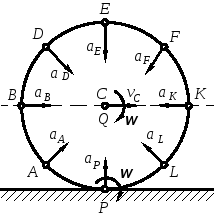
Рассмотрим,
например, качение без скольжения колеса
по прямолинейному рельсу с постоянной
скоростью центра
(рис. 8).
Мгновенный центр скоростей Р находится в точке соприкосновения колеса с рельсом. Поэтому:
vC = PC ω = R·ω,
где R – радиус колеса.
Угловая скорость вращения колеса:
.
Центр колеса движется равномерно по прямой, следовательно, его ускорение:
аС = 0,
т. е. центр колеса является мгновенным центром ускорений.
Так как колесо вращается равномерно, то ускорения всех точек колеса равны центростремительным ускорениям этих точек в их вращательном движении вокруг мгновенного центра ускорений. Например, ускорения точек обода определяются:
.
Ускорение
каждой точки колеса направлено к
мгновенному центру ускорений. В
рассмотренном примере наглядно видно,
что мгновенный центр скоростей Р
и мгновенный центр ускорений Q
является различными точками плоской
фигуры. Мгновенный центр скоростей, не
имея в данный момент скорости, имеет
ускорение
,
мгновенный центр ускорений, не имея в
данный момент ускорения, имеет постоянную
скорость
.
2.2.2.
Случай В.
Известны
модуль и направление ускорения какой-либо
точки А плоской фигуры
,а также
угловая скорость
и угловое ускорение
фигуры.
Определим положение мгновенного центра ускорений.
а)
Неравномерное вращение:
ω ≠ 0; ε ≠ 0. В этом случае мгновенный
центр ускорений находится на отрезке,
составляющем с направлением ускорения
,
угол
,
(9)
который
отложен от ускорения точки в сторону
,
на расстоянии от точкиА,
равном:
(10)
На рис. 9 показан случай ускоренного вращения плоской фигуры, а на рис. 10 – случай замедленного вращения.
|
| |
|
Рис. 9 |
Рис. 10 |
Как
видно, направление вращения на построение
угла 
не
влияет и угол
всегда откладывается от направления
ускорения в сторону
.
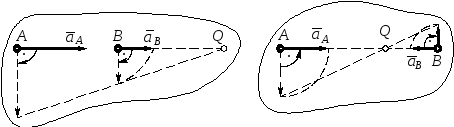
б)Равномерное вращение: ω ≠ 0, ε = 0 (также момент, когда ε = 0 при неравномерном вращении) (рис. 11).
|
| |
|
Рис. 11 |
Рис. 12 |
В этом случае:
и
= 0,
т. е. ускорения всех точек направлены к мгновенному центру ускорений. Расстояние от точки до мгновенного центра ускорений определяется по
формуле:
.
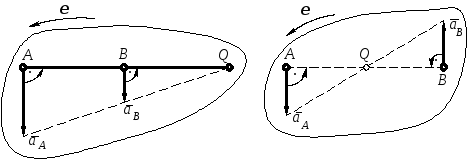
в) Момент, когда угловая скорость становится равной нулю: ω = 0,
ε ≠ 0. В этом случае:
,
= 90,
т. е. ускорения всех точек направлены перпендикулярно к отрезкам, соединяющим эти точки с мгновенным центром ускорений (рис. 12).
Расстояние от точки до мгновенного центра ускорений определяется по формуле:
.
(11)
Угловая скорость фигуры обычно обращается в нуль при изменении направления вращения фигуры.
г) Момент, когда угловая скорость и угловое ускорение становится равными нулю при непоступательном движении ω = 0, ε = 0.
В этом случае ускорения всех точек плоской фигуры в данный момент геометрически равны, так как ускорение любой точки равно ускорению полюса (рис. 13).
.
|
| |
|
Рис.13. |
Рис. 14. |
2.2.3.
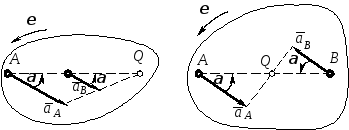
Случай С. Известны
модули и направления ускорений двух
точек плоской фигуры.
Допустим, что известны ускорения точек
А
и В
плоской фигуры
и
(рис. 14).
Примем точку А за полюс, тогда на основании (4) можно получить:
.
Построим
при точке В
параллелограмм ускорений по заданной
диагонали
и
одной из сторон
.
Другая сторона параллелограмма опре-
делит
ускорение
во вращении точкиВ
фигуры вокруг полюса А.
Ускорение
составляет угол
с отрезкомАВ,
соединяющим точку В
с полюсом А.
Отсчитывая
полученный угол 
от ускорения
к отрезку АВ,
получаем направление
,
в данном случае противоположное
направлению вращения часовой стрелки.
Определив угол
и направление
,
отложим этот угол от ускорений точек
А и В
по направлению
.
Две полученные полупрямые продолжим
до пересечения в точкеQ,
которая и будет мгновенным центром
ускорений.
Этот
способ определения положения мгновенного
центра ускорений не требует определения
угла 
путем
вычислений. Если положение мгновенного
центра ускорений по этому способу
определяется графически, то ускорения
точек должны быть отложены в масштабе
по их истинным направлениям.
|
| |
|
Рис.15 |
Рис. 16 |
Рассмотрим случаи, когда ускорения точек плоской фигуры параллельны. Положение мгновенного центра ускорений в этом случае определяется на основании того, что:
модули ускорений точек пропорциональны длинам отрезков, соединяющих точки с мгновенным центром ускорений:
ускорения точек составляют с отрезками, соединяющими точки с мгновенным центром ускорений, один и тот же угол
.
На рис. 15 и 16 выполнено построение для случая:
0
<
<
90,
т. е. ω
≠ 0, ε
≠ 0.
Рис. 17 и 18 соответствуют случаю α = 90,
,
ω
= 0, ε
≠ 0.
|
| |
|
Рис.17. |
Рис. 18. |
На рис. 19 и рис. 20 построен мгновенный центр ускорений для случая:
=0,
,
ε
= 0, ω
≠ 0.
В
случае
(рис. 21) мгновенный центр ускорений
находится в бесконечности, а ускорения
всех точек плоской фигуры геометрически
равны.
|
| |
|
Рис. 19 |
Рис. 20 |
|
| |
|
Рис. 21 | |
