2.2. Различные случаи определения положения мгновенного центра скоростей.

а

Рис. 1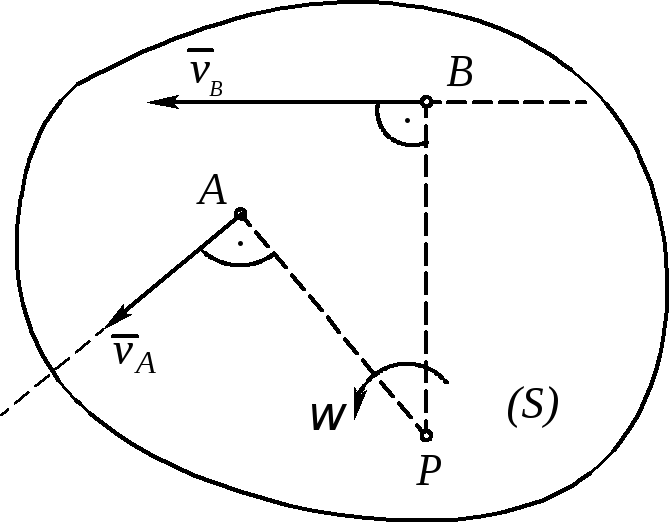

) Допустим, что известны прямые, по которым направлены скорости двух точек плоской фигуры А и В (рис. 1). Тогда мгновенный центр скоростей фигуры определится как точка пересечения перпендикуляров к этим прямым, восставленным в точках А и В. Зная модуль скорости точки А и определив расстояние этой точки от мгновенного центра скоростей РА, находим угловую скорость плоской фигуры согласно зависимости (3):

.

Модуль скорости точки В можно определить из пропорциональности скоростей точек их расстояниям до мгновенного центра скоростей по формуле:

,

откуда ,

или при помощи угловой скорости фигуры согласно (3):

.

Скорость любой другой точки плоской фигуры определяется аналогично.

б) Если скорости точек А и В плоской фигуры параллельны между собой и перпендикулярны к АВ, то для определения положения мгновенного центра скоростей должны быть известны модули скоростей обеих точек А и В (рис. 2, а и б).

Известно, что модули скоростей точек фигуры пропорциональны их расстояниям от мгновенного центра скоростей, т. е.:

.

а) б) в)

Рис.2

Следовательно, концы скоростей точек А и В лежат на прямой, проходящей через мгновенный центр скоростей. Пересечение этой прямой с прямой АВ определяет мгновенный центр скоростей фигуры.

Если скорости точек А и В плоской фигуры равны, параллельны между собой и перпендикулярны к АВ (рис. 2, в)), то мгновенный центр скоростей находится в бесконечности (АР = ∞). Очевидно, что в этом случае:

.

в) Если известно, что скорости двух точек А и В плоской фигуры параллельны и не перпендикулярны к АВ (рис. 3), то мгновенный центр скоростей находится в бесконечности (АР = ∞). Очевидно, что и в этом случае:

.

Расстояние от всех точек плоской фигуры до мгновенного центра скоростей, в этом случае, равны между собой:

АР = ВР = …= ∞.

Поэтому скорости точек плоской фигуры в рассматриваемый момент геометрически равны:

г

Рис. 3 Рис. 4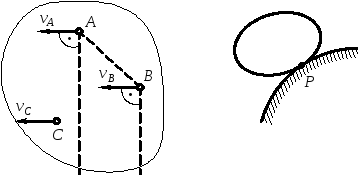

) На практике часто происходит движение плоской фигуры, при котором она катится без скольжения по некоторой неподвижной линии (рис. 4). В этом случае мгновенный центр скоростей плоской фигуры находится в точке ее соприкосновения с линией. Действительно, при отсутствии скольжения скорость точки соприкосновения плоской фигуры по отношению к неподвижной кривой равна нулю, т. е. эта точка в данный момент времени является мгновенным центром скоростей.

3. Примеры решения задач

Задача 1. К кривошипу ОА, равномерно вращающемуся с угловой скоростью _ОА = 4 с ^-1, прикреплен шатун АВ, соединенный с коромыслом ВС. ОА = r =0,5 м; АВ = 2r =1,0 м; ВС = r  2, м,  ОАВ = 90; АВС = 45. Определить для этого положения механизма скорость точки В шатуна, его угловую скорость, а также скорость точки Д, лежащей на середине шатуна АВ.

Задачу решим двумя способами, основанными на двух различных подходах (см. п. 2.1.).

Рис. 5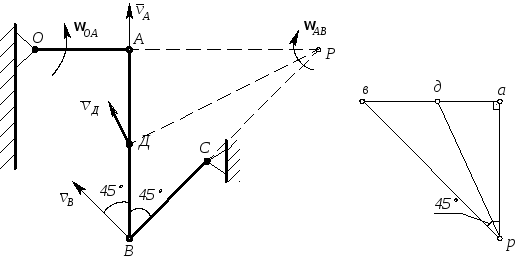

Первый способ (основан на построении плана скоростей).

1. Определяем скорость точки А. v_A = _OA  r = 4· 0,5 = 2 м/с. Так как точка А принадлежит к кривошипу, совершающему вращательное движение, направлен вектор скорости точки А по направлению стрелки _OA перпендикулярно к кривошипу ОА,

2. Из произвольно выбранного полюса, точки Р, откладываем в масштабе вектор скорости точки А (отрезок ра).

3. Точка В принадлежит двум звеньям механизма: шатуну АВ, совершающему плоское движение и коромыслу ВС, совершающему вращательное движение. Относительно коромысла ВС нам известно направление скорости точки В ( к ВС). Из полюса, точки р проводим линию перпендикулярную к коромыслу ВС.

4. По теореме о скоростях точек тела:

,

Из точки а плана скоростей проводим линию, перпендикулярную к шатуну АВ. На пересечении с проведенной ранее линией получим точку в плана скоростей. Тогда отрезок вр выразит скорость точки В, а отрезок ав – вращательную скорость шатуна АВ. Так как план скоростей представляет собой прямоугольный равнобедренный треугольник, из него можно легко найти модули искомых скоростей:

м/с,

м/с.

Угловая скорость .

Скорость точки Д определим из пропорции в соответствии с ее положением на звене АВ (см. рис. 5). Модуль скорости точки Д равен

Скорость точки Д на плане скоростей определяется отрезком рд.

Второй способ (основан на понятии мгновенного центра скоростей).

1. Построим мгновенный центр скоростей звена АВ, восстановив перпендикуляры к скоростям точек А и В. Получим АВР прямоугольный и равнобедренный с углом 45 у основания. Определим стороны треугольника по известным углам и длине катета АВ:

АР = АВ = 2r = 1,0 м,

м.

2. Определим угловую скорость звена АВ в его вращательном движении относительно МЦС точки Р. Для этого скорость точки А разделим на расстояние АР:

.

Покажем направление _АВ стрелкой относительно точки Р.

3. Определим модуль скорости точки В:

v_B = _AB  BP = 2,0  1,41 = 2,82 м/с.

Направлен вектор скоростей точки В перпендикулярно к ВР по направлению стрелки _АВ.

4. Определим модуль скорости точки Д:

v_Д = _AB  ДP = 2,0  1,12 = 2,24 м/с.

Направлен вектор скоростей точки В перпендикулярно к ДР по направлению стрелки _АВ.

Сравнение результатов решения задачи двумя способами показывает, что они идентичны.

Проиллюстрируем здесь также применение следствия из теоремы. Для скоростей точек А и В в проекции на звено АВ можно записать

Откуда

Данный результат также совпадает с полученным выше решением.

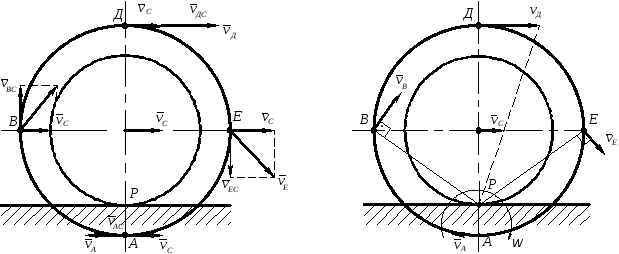
Задача 2. Цилиндр радиусом r = 0,4 м катится по плоскости без скольжения. Скорость точек его оси v_c = 0.4 м/с. Диск радиусом R = 0,5 м жестко соединен с цилиндром в сечении, где плоскость не препятствует его движению. Определить угловую скорость системы цилиндр-диск, а также скорости точек А, В, Д, Е, расположенных на двух перпендикулярных диаметрах диска.

Определяем угловую скорость диска как отношение скорости точки С к расстоянию от точки до МЦС (мгновенный центр скоростей находится в точке контакта цилиндра радиусом r с неподвижной поверхностью):

.

Далее решаем задачу двумя способами.

Первый способ (основан на теореме о скоростях точек тела).

Скорости точек А, В, Д, Е определяем, как геометрическую сумму скорости полюса (точки С) и вращательной скорости каждой из точек относительно полюса:

,

,

,

.

Так как расстояние от точек А, В, Д, Е до полюса одинаково и равно R, то модули вращательных скоростей будут равны между собой.

.

Направлены эти векторы перпендикулярно соответствующим радиусам (см. рис. 6). При сложении составляющих векторов скоростей точек В, Е видим, что они направлены друг к другу под прямым углом. Следовательно, результирующий вектор можно определить по правилу параллелограмма, а его модуль по теореме Пифагора:

,

.

Составляющие скоростей точек А и Д лежат на одной прямой, поэтому

модуль результирующего вектора скорости точки можно определить при

алгебраическом их сложении с учетом направления:

,

.

Знак «минус» у скорости точки А показывает направление вектора скорости этой точки, по отношению к скорости полюса.

Второй способ (основан на понятии мгновенного центра скоростей).

По направлению скорости точки С относительно МЦС точки Р определяем направление угловой скорости диска. Применение понятия «мгновенный центр скоростей» позволяет рассматривать плоскопараллельное движение твердого тела как мгновенное вращательное относительно оси, проходящей через МЦС. Угловая скорость диска в данной задаче уже определена, необходимо определить расстояния от точек А, В, Д, Е до точки Р (МЦС):

AP = R – r = 0,5 – 0,4 = 0,1 м,

ДP = R + r = 0,5 + 0,4 = 0,9 м,

.

Скорости точек по модулю и направлению определяем в соответствии с системой (3):

v_A = ω  AP = 1,0  0,1 = 0,1 м/c,

v_B = ω  BP = 1,0  0,64 = 0,64 м/c,

v_Д = ω  ДP = 1,0  0,9 = 0,9 м/c,

v

Рис. 6.

_Е = ω  ЕP = 1,0  0,64 = 0,64 м/c.

Сравнение результатов решения задачи двумя способами показывает, что они идентичны.