Bilety / 48

48.Производная по направлению. Градиент функции и его свойства. Поверхности уровня, их свойства. Примеры.

В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (т.е. точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению .

Рассмотрим функцию от аргументов в окрестности точки . Для любого единичного вектора определим производную функции в точке по направлению следующим образом:

Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора .

Градиент (от лат. gradiens, род. падеж gradientis — шагающий) — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».

Как видно из объяснения, градиент является векторной функцией, а величина, которую он характеризует — функцией скалярной.

Формально, для случая трёхмерного пространства, градиентом называется векторная функция с компонентами , , , где φ — некоторая скалярная функция координат x, y, z.

Если — функция n переменных , то её градиентом будет n-мерный вектор

,

компоненты которого равны частным производным по всем её аргументам.

Градиент обозначается или, с использованием оператора набла, .

Из определения градиента следует, что:

Свойства: Для любого постоянного числа и скалярных полей справедливо следующее:

• 

Линейность

• 

• 

Правило Лейбница

• , где — скалярное произведение векторов 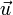и .

Пример : Например, градиент функции будет представлять собой:

Поверхность уровня: Определение 8.3   Пусть функция задана в некоторой области пространства , . Поверхность в пространстве , определённая уравнением , где  -- постоянная, называется поверхностью уровня функции . Если , то множество, заданное уравнением , называется линией уровня.     

Пример 1.

   Вычислитьпроизводную функции z = x² + y²·x в точке М(1; 2) по направлению вектора , где М₁ – точка с координатами (3; 0).    Решение. Найдем единичный вектор , имеющий данное направление

, , ,

откуда . Вычислим частные производные функции в точке М (1; 2)

, .

По формуле получим 

Пример 2

Дана функция трёх переменных , точка M₀(1, 2, 1) и вектор .    Найти:

grad u в точке М₀. Для этого вычислим частные производные и воспользуемся определением градиента

, , , — искомый градиент.