Bilety / 8

Связь между дифференцируемостью и непрерывностью функции

Рассмотрим следующие вопросы, который касаются функций.

Если функция непрерывна, то она дифференцируема?

Если функция дифференцируема, то она непрерывна?

Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.

Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность.

Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт.

Найдем производную следующей функции . Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:

Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:

данный предел равен 1, если и равен (-1), если , получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема.

Необходимый признак дифференцируемости

Если функция f(x) дифференцируема в точке x₀, то она непрерывна в этой точке.

Из непрерывности самой функции в точке x₀ не следует дифференцируемость ее в этой точке.

Геометрический смысл дифференцируемости функции. 

Напомним, что для функции одной переменной  из дифференцируемости функции в точке  следует существование касательной к графику функции в точке .

         Рассмотрим непрерывную функцию двух переменных , . График этой функции, т.е. множество точек , представляет собой поверхность в пространстве . Пусть плоскость  проходит через точку  поверхности ;  – произвольная (текущая) точка поверхности ;  – ос

нование перпендикуляра, проведенного из точки  к плоскости  (рис. 6).

Рис. 6.

         Определение. Плоскость , проходящая через точку  поверхности , называется касательной плоскостью к поверхности  в этой точке, если при  () величина  является бесконечно малой более высокого порядка, чем , т.е. .

         Теорема 8. Если функция  дифференцируема в точке , то в точке  существует касательная плоскость к поверхности  (графику этой функции), причем уравнение касательной плоскости имеет вид

.

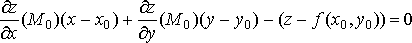         Вектор  нормали к касательной плоскости, т.е. , называется вектором нормали (или нормалью) к поверхности.