Bilety / 9

Основные правила дифференцирования. Сумма.

      Выведем несколько правил вычисления производных, В этом пункте значения функций u и v и их производных в точке х₀ обозначаются для краткости так: u(х₀) = u, v(х₀) = v, u'(х₀) = u', v'(х₀)=v`. Если функции u и v дифференцируемы в точке х₀, то их сумма дифференцируема в этой точке и

(u+v)' = u' + v'.

      Коротко говорят: производная суммы равна сумме производных.       1) Для доказательства вычислим сначала приращение суммы функций в рассматриваемой точке: Δ(u+v) = u (х₀+Δx)+ v(х₀+Δx) – (u(х₀)+v(х₀)) = (u(х₀+Δx)-u(х₀)) + (v(х₀+Δx)-v(х₀)) = Δu + Δv       2)

      3) Функции u и v дифференцируемы в точке х₀, т. е. при Δх→0

      Тогда

при Δх→0 (см. правило 3, а) предельного перехода), т. е. (u+v)' = u'+v’

Основные правила дифференцирования. Произведение.

      Если функции и и v дифференцируемы в точке х₀, то их произведение дифференцируемо в этой точке и

(uv)' = u'v+uv'.

      1) Найдем сначала приращение произведения:

Δ(uv) = u(х₀+Δx)v(х₀+Δx)-u(х₀)v(х₀)=(u(х₀)+ Δu)(v(х₀)+ Δv)-u(х₀)v(х₀) =

=u(х₀)v(х₀)+ Δuv(х₀)+u(х₀) Δv+ΔuΔv-u(х₀)v(х₀)= Δuv(х₀)+u(х₀) Δv+ΔuΔv

      2)

      3) В силу дифференцируемости функций u и v в точке х₀ при Δx→0 имеем

      Поэтому

т. е. (uv)' = u'v+uv', что и требовалось доказать.       Следствие. Если функция u дифференцируема в х₀, а С — постоянная, то функция Сu дифференцируема в этой точке и

(Сu)' = Сu'.

      Коротко говорят: постоянный множитель можно выносить за знак производной.       Для доказательства воспользуемся правилом 2 и известным из пункта о производной, фактом С' = 0:

(Сu)' = Сu' + С'u = Cu' + 0⋅u = Cu'.

Пример.

Продифференцировать функцию .

Решение.

В данном примере . Применяем правило производной произведения:

Обращаемся к таблице производных основных элементарных функций и получаем ответ:

Основные правила дифференцирования. Частное

Если функции u и v дифференцируемы в точке x₀ и функция v не равна нулю в этой точке, то частное u/v также дифференцируемо в x₀ и

Выведем сначала формулу

1) найдем приращение функции 1/v:

2) Отсюда

3) При Δx→0 имеем Δv/Δx→v’ (в силу дифференцируемости v в точке x₀), Δv→0 (по доказанной лемме). Поэтому

Теперь, пользуясь правилом нахождения производной произведения функций, находим производную частного:

Пример.

Выполнить дифференцирование функции .

Решение.

Исходная функция представляет собой отношение двух выражений sinx и 2x+1. Применим правило дифференцирования дроби:

Не обойтись без правил дифференцирования суммы и вынесения произвольной постоянной за знак производной:

Производная сложной функции.

Если функция f имеет производную в точке х₀, а функция g имеет производную в точке y₀=f(x₀)y то сложная функция h(х) = g(f(х)) также имеет производную в точке х₀, причем

h’(x₀) = g’(f(x₀))•f’(x₀) (1)

Для доказательства формулы (1) надо (как и раньше) при Δx≠0 рассмотреть дробь Δh/Δx и установить, что

при Δx→0. Введем обозначения:

Δy = f(x₀+Δx)-f(x₀)= Δf

Тогда Δh = h(х₀ + Δх) - h(x₀) = g(f(x₀ +Δx)) - g(f(x₀)) = g(y₀ + Δy) - g(y₀) = Δg. Δy→0 при Δx→0, так как f дифференцируема в точке x₀. Далее доказательство мы проведем только для таких функций f, у которых Δf≠0 в некоторой окрестности точки х₀. Тогда

при Δx→0, так как Δf/Δx→f’(x₀) при Δx→0, а Δg/Δy→g’(y₀) при Δy→0, что выполнено при Δx→0.

Пример.НА ВСЯКИЙ СЛУЧАЙ !! ! ! !!! http://www.mathelp.spb.ru/book1/proizvodnaya.htm

Производная обратной функции.

Пусть функция дифференцируема и строго монотонна на . Пусть также в точке производная . Тогда в точке   определена дифференцируемая функция , которую называют обратной к  , а ее производная вычисляется по формуле .

Примеры.

Найти производную обратной тригонометрической функции y = arcsinx.  Обратная функция  x = siny и , по формуле для обратной функции .

Найдем  функции  y = arctgx. Обратная функция  x = tgy, 

Производная суммы, производная разности.

Для доказательства второго правила дифференцирования воспользуемся определением производной и свойством предела непрерывной функции.

Подобным образом можно доказать, что производная суммы (разности) n функций равна сумме (разности) n производных 

Пример.

Найти производную функции 

Решение.

Упростим вид исходной функции 

Используем правило производной суммы (разности): 

В предыдущем пункте мы доказали, что постоянный множитель можно выносить за знак производной, поэтому

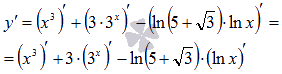
Осталось воспользоваться таблицей производных: