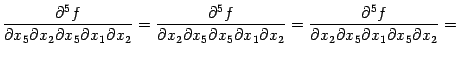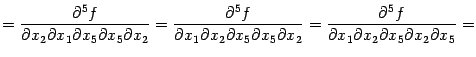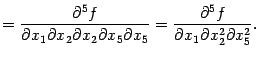Bilety / 44

44.Частные производные высших порядков. Теорема о смешанных производных (независимость результата дифференцирования от порядка дифференцирования).

Теорема о смешанных производных

   Ответ на вопрос о том, при каких условиях значения смешанных производных не зависят от того, в каком порядке производится дифференцирование, дает следующая теорема.    Теорема. Предположим, что:

1. f (x, y ) определена в некоторой (открытой) области D;

2. в этой области существуют производные , а также вторые смешанные производные ,

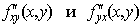3. эти смешанные производные как функции х и у непрерывны в некоторой точке (х₀, у₀) области D .

Тогда в этой точке имеет место равенство .    Доказательство. Рассмотрим выражение

где Δ х и Δ у — любые столь малые числа, что точка M₁(x₀ + Δ x, y₀ + Δ y) находится в указанной области D . Введем вспомогательную функцию

φ (x) = f (x, y₀ + Δ y) − f (x, y₀);

тогда выражение А можно рассматривать как приращение дифференцируемой на отрезке [х₀, х₀ + Δ х] функции φ(х) одной переменной х:

A = Δ φ = φ (x₀ + Δx) − φ (x₀)

Поэтому, применяя к этой разности теорему Лагранжа, запишем

где 0 < θ₁ < 1. Выражение в квадратных скобках можно рассматривать как приращение дифференцируемой на отрезке [у₀, у₀ + Δ у] функции  одной переменнойу. Применяя еще раз теорему Лагранжа (по переменной у), получаем

                     (5)

   С другой стороны, если вести вспомогательную функцию ψ (y) = f (x₀ + Δ x, y) − f (x₀, y), то, поступая аналогично, получим

A = Δ ψ = ψ (y₀ + Δ y) − ψ (y₀)

а затем

                     (6)

Сравнивая (5) и (6), получаем

.

   Переходя теперь в этом равенстве к пределу при Δ х → 0, Δ у → 0 и учитывая непрерывность частных производных  f ''_yx(x, y), f ''_xy(x, y) в точке М, получим

или

   Вопрос о существовании и равенстве смешанных производных тождественен с вопросом о существовании и равенстве повторных пределов для выражения А.

Пример 7.17   Если две производных

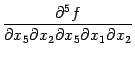
и

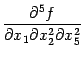
непрерывны, то они совпадают, так как соответствующие списки номеров переменных равны, соответственно,  и  и отличаются лишь порядком перечисления номеров. Значит, частные производные отличаются лишь порядком дифференцирований, и поэтому

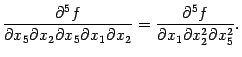
В этом примере перестановки дифференцирований можно выполнить в следующем порядке:

При первой и четвёртой перестановках переставляемые диффиеренцирования -- внешние и выполняются непосредственным применением теоремы к функциям 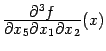 и 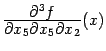соответственно; эти производные третьего порядка предполагаются непрерывными. При остальных перестановках переставляются внутренние дифференцирования. При этом, например, при второй перестановке, рассуждаем так: имеем равенство

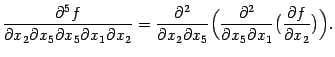
Функци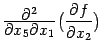и  и  непрерывны по предположению, так как содержат меньше дифференцирований по  и  , чем исходные производные пятого порядка, и столько же дифференцирований по остальным переменным. Поэтому

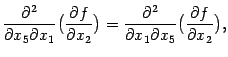
и мы можем продолжить равенство:

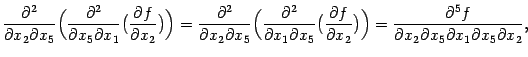
и вторая перестановка обоснована.