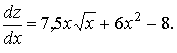Bilety / 40

40. Теорема о полной производной. Частные производные сложной ФНП. Примеры.

ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ЧАСТНЫЕ ДИФФЕРЕНЦИАЛЫ

Для упрощения записи и изложения мы ограничимся случаем функций от трех переменных; все дальнейшее, однако, справедливо и для функций любого числа переменных.

Итак, пусть в некоторой (открытой) области D имеем функцию u=f(x, y, z); возьмем точку M₀(x₀, y₀, z₀) в этой области.

Если мы припишем у и z постоянные значения у₀ и z₀ и будем изменять х, то u и будет функцией от одной переменной х (в окрестности х₀); можно поставить вопрос о вычислении ее производной в точке х=х₀.

Придадим этому значению x₀ приращение ∆х, тогда функция получит приращение:

которое можно было бы назвать ее частным приращением (по х), поскольку оно вызвано изменением значения лишь одной переменной. По самому определению производной, она представляет собою предел

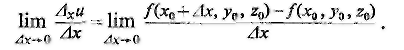
Эта производная называется частной производной функции f(x, y, z) по х в точке (х₀, y₀, z₀).

Как видим, в этом определении не все координаты равноправны, так как у₀ и z₀ наперед фиксированы, а х меняется, стремясь к х₀.

Частную производную обозначают одним из символов:

Заметим, что буква х внизу в этих обозначениях лишь указывает, по какой из переменных берется производная, и не связана с тем, в какой точке (х₀, у_0, z₀) мы производную вычисляем. И здесь цельные символы можно рассматривать как функциональные обозначения для частной производной по х. Подобных примечаний впредь мы повторять уже не станем.

Аналогично, считая х и z постоянными, а у переменным, можно рассматривать предел

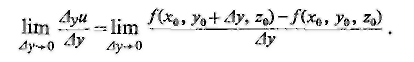
Предел этот называется частной производной функции f(x, y, z) по у в точке (х₀, у₀, z₀) и обозначается символами, аналогичными предыдущим:

Точно так же определяется и частная производная функции f(x, y, z) по z в точке (х₀, у₀, z₀).

Самое вычисление частной производной по существу не представляет ничего нового по сравнению с вычислением обыкновенной производной.

получаем так называемую формулу "полной производной":

Эта же формула "полной производной" в случае:

примет вид:

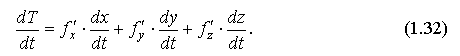
Возможны и иные вариации формул (1.27) - (1.32).

Замечание: формула "полной производной" используется в курсе физики, раздел "Гидродинамика" при выводе основополагающей системы уравнений движения жидкости.

Пример 1.10. Дано:

Найти

Решение

Согласно (1.31): 

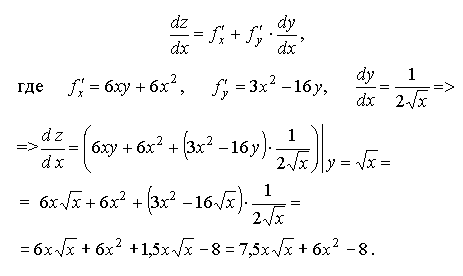
Ответ: