
- •ПРЕДИСЛОВИЕ
- •Глава 1. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- •Лабораторная работа № 1
- •Лабораторная работа № 2
- •Лабораторная работа №3
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Высота
- •подъема
- •груза
- •Контрольные вопросы
- •Лабораторная работа № 5
- •Лабораторная работа № 6
- •Таблица 4.15
- •Обработка результатов прямых измерений
- •Результаты вычислений
- •Таблица 5.2
- •Параметры лабораторной установки
- •Таблица 5.3
- •Результаты эксперимента и обработки результатов
- •Стальной брус
- •Латунный брус
- •6.1. Гармонические колебания
- •6.2 Затухающие колебания
- •6.3 Вынужденные колебания
- •Лабораторная работа № 9
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 10
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №11
- •Цель работы
- •Описание лабораторной установки
- •Содержание работы
- •Методика эксперимента
- •Порядок выполнения работы
- •Определение периода собственных колебаний маятника
- •Изучение вынужденных колебаний маятника
- •Обработка результатов измерений
- •Контрольные вопросы
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика проведения эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Цель работы
- •Содержание работы
- •Описание моделирующей программы
- •Порядок выполнения работы
- •Анализ результатов моделирования
- •Контрольные вопросы
- •ГЛАВА 7. ВОЛНОВОЕ ДВИЖЕНИЕ
- •Методика эксперимента и описание установки
- •Контрольные вопросы
- •Описание лабораторной установки
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №18
- •Цель работы
- •Содержание работы
- •Методика проведения численного эксперимента на ЭВМ
- •Порядок выполнения работы
- •Завершение работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №19
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Таблица 9.1
- •Таблица 9.2
- •Таблица 9.3
- •Глава 10. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
- •10.1. Поведение молекул в приповерхностном слое жидкости
- •10.2. Коэффициент поверхностного натяжения
- •10.3. Давление под изогнутой поверхностью жидкости
- •10.4. Краевой угол
- •Добавочное давление под изогнутой поверхностью
- •Поэтому высота жидкости в капилляре равна
- •Лабораторная работа № 22
- •Цель работы
- •Содержание работы
- •Порядок выполнения работы
- •Обработка результатов измерения
- •Контрольные вопросы
- •ОГЛАВЛЕНИЕ
Таблица 4.9
|
|
|
|
|
|
Положение светового "зайчика" |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Расстояние |
|
|
|
на шкале |
|
|
|
|
Расстояние |
|
|
|
|
|
||||||
|
|
|
от центра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Положение |
Начальное |
|
При max отклоне- |
/n0–n/, |
|
от оси |
|
φ, рад |
|
|
||||||||||||
|
грузов |
|
груза |
|
(до выстрела), n0 |
нии, n |
|
м |
|
маятника до |
|
|
|||||||||||
|
|
до оси |
|
|
|
|
|
||||||||||||||||
|
|
|
r, м |
|
|
|
|
|
|
|
|
|
|
|
|
шкалы, l, м |
|
|
|
|
|
||
|
|
|
|
делений |
|
м |
|
делений |
|
м |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.10 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Расстояние |
|
Масса |
Масса |
Расстояние |
|
Время 10 |
|
|
Период |
|
Скорость |
|
|||||||||
Положение |
от центра |
|
одного |
пули |
|
от пробоины |
|
полных |
|
колебаний |
|
|
пули |
|
|||||||||
|
грузов |
груза до |
|
груза |
|
в мишени до |
|
колебаний |
|
|
v, |
<v>, |
|
||||||||||
|
|
m, кг |
|
|
|
|
Т, с |
|
|
||||||||||||||
|
|
оси, r, м |
|
m0, кг |
|
|
|
|
оси h, м |
|
t, с |
|
|
|
|
м/с |
м/с |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Можно ли пользоваться приведенной в работе теорией, если удар пули о мишень происходит под непрямым углом?
2.Какие факторы могут влиять на точность эксперимента в данной работе?
3.При каком допущении систему "маятник–пуля" можно считать замкнутой?
4.Сформулируйте и запишите основной закон динамики вращательного движения. Что называется моментом силы, импульсом момента силы?
5.Какой удар называется неупругим? Какие законы сохранения выполняются, при неупругом ударе?
6.Сформулируйте закон сохранения момента импульса и запишите его для системы "маятник – пуля". Чему равен момент импульса материальной точки и момент импульса тела?
7.Какие превращения энергии происходят после удара в данной работе? Запишите закон сохранения энергии в применении к системе "маятник–пуля".
8.Как вычисляется момент инерции любого твердого тела? Запишите, чему равен момент инерции системы "крестовина–груз"? Как можно его изменить?
9.На чем основан метод определения скорости пули с помощью крутильно– баллистического маятника?
10.Как связан период колебаний с моментом инерции крутильно–баллистического маятника?
Лабораторная работа № 5
ИЗУЧЕНИЕ УПРУГОГО СОУДАРЕНИЯ ДВУХ ШАРОВ
Цель работы
Изучение упругого удара на примере соударения двух металлических шаров. Измерение времени удара шаров, определение средней силы их
65
взаимодействия (удара), радиуса контактной площадки и коэффициента восстановления после упругого соударения шаров. Проверка законов сохранения энергии и импульса.
Содержание работы
Ударом называется явление конечного изменения скоростей взаимодействующих твердых тел за малый промежуток времени, происходящее при их столкновении.
При соударении тел происходит их деформация, что приводит к возникновению упругих сил, изменяющих скорости этих тел. В зависимости от материала, из которого сделаны тела, эти силы могут быть связаны как с самой деформацией, так и со скоростью этой деформации, или с тем и другим вместе. Поэтому различают три типа ударов: абсолютно упругий, аб-
солютно неупругий и неупругий.
Удар называется абсолютно упругим, если в результате не происходит превращения механической энергии соударяющихся тел (например, шаров) в другие виды энергии. Для того, чтобы удар был абсолютно упругим все силы, возникающие в телах, должны зависеть только от абсолютного значения деформации, а не от скорости этой деформации (например, не должны возникать силы подобные силам трения). При этом, когда относительная скорость двух тел при ударе обращается в нуль, а деформация достигает максимума, взаимодействие продолжается до полного исчезновения деформаций и тела снова приобретают относительную скорость. К этому времени силы упругости совершат такую же положительную работу, какая была затрачена на деформацию. Потенциальная энергия деформированных тел полностью перейдет в кинетическую энергию их относительного движения.
Перейдем к более подробному изучению простейшего случая абсолютно упругого удара – центрального удара шаров. Удар шаров называет-
ся центральным, если векторы начальных скоростей шаров v1 и v2 лежат
на прямой, соединяющей их центры. В противном случае удар называется нецентральным. При нецентральном ударе шары разлетаются под углом к
исходным векторам v1 и v2 .
Рассмотрим два массивных стальных шара, подвешенных на бифилярных (двунитных) подвесах. Шары движутся так, что при соударении их скорости направлены вдоль прямой, соединяющей их центры. Это позволяет вместо векторов v рассматривать равные им проекции v на ось, проходящую через центры шаров.
При абсолютно упругом ударе выполняются законы сохранения импульса и энергии системы двух взаимодействующих тел:
66

mv |
1 |
+ m v |
2 |
= m u + m u |
, |
|
|
|
|||||||||
|
1 |
|
|
2 |
|
|
1 |
1 |
2 |
2 |
|
|
|
|
|||
m1v12 |
+ |
m2v |
2 |
2 |
= |
m1u12 |
+ |
m2u2 |
2 |
; |
(4.68) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
2 |
|
|
2 |
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где v1 , v2 и u1 , u2 – скорости шаров 1 и 2, соответственно, до и после уда-
ра; m1 и m2 – массы шаров. Отметим, что все указанные скорости рассматриваются в лабораторной (то есть неподвижной относительно наблюдателя) системе отсчета.
Зная массы и скорости шаров до удара можно найти их скорости после удара, для чего необходимо решить систему (4.68) относительно u1 и u2. Записывая уравнения системы (4.68) в проекциях на оси и преобразуя их, приходим к следующей системе уравнений:
m1 (v1 −u1) = m2 (u2 −v2 ), |
|
||||||
m (v 2 |
−u2 ) = m (u2 |
−v 2 ); |
(4.69) |
||||
|
1 |
1 |
1 |
2 |
2 |
2 |
|
или |
|
|
|
|
|
|
|
m (v |
|
−u ) = m (u |
|
−v |
|
), |
|
||
|
1 |
1 |
1 |
2 |
2 |
|
2 |
|
(4.70) |
m1(v1 −u1 )(v1 +u1) = m2 (u2 −v2 )(u2 +v2 ). |
|
||||||||
Подставляя левую часть первого уравнения (4.69) в уравнение (4.70) и |
|||||||||
сокращая получившееся выражение на ненулевую скобку (u2 −v2 ) , получим
v1 + u1 =v2 + u2 . |
(4.71) |
Решая теперь первое уравнение системы (4.69) и уравнение (4.71) со- |
|
вместно и выполнив несложные преобразования, получим выражения для скоростей шаров после удара:
u = 2 |
m1v1 + m2v2 |
|
−v |
, |
||||
|
|
|||||||
|
1 |
|
|
m1 |
+ m2 |
1 |
|
|
|
|
|
|
|
|
(4.72) |
||
|
|
|
|
m1v1 |
+ m2v2 |
|
|
|
|
|
|
|
|
|
|
||
u2 |
= 2 |
|
|
|
|
−v2 . |
||
|
m1 + m2 |
|
||||||
|
|
|
|
|
|
|
||
Если массы шаров одинаковы, то из выражения (4.72) следует, что u1 = v2, u2 = v1, то есть шары обмениваются скоростями.
При абсолютно упругом центральном ударе шара 1 о такой же неподвижный шар 2, первый останавливается, теряя импульс р = mv1. Из второ-
го закона Ньютона: F τ = ∆p = mv1 , где τ – время контакта шаров при уда-
ре (время удара), находим среднюю силу взаимодействия шаров за время τ (среднюю силу удара):
F = |
mv |
1 . |
(4.73) |
τ |
67

Время контакта τ в работе измеряется электронным секундомером. Величина F τ называется импульсом силы. Очевидно, что при ударе ве-
личина силы взаимодействия сначала увеличивается oт нуля (в начале контакта) до максимального значения (при максимальном сжатии шаров), а затем уменьшается до нуля.
Оценим характерную величину давления
при ударе Р = Fmax/S, где S=πr2 – максимальная
площадь контакта при взаимном сжатии шаров,
r – радиус контактной Рис. 4.16 площадки (рис. 4.16, а).
Из рис. 4.16, б видно, что
r = R2 −(R −δ )2 ≈  2Rδ
2Rδ
(считая, что δ << R, где R – радиусы шаров). Деформация δ это расстояние, на которое смещается шар 1 за первую половину удара, то есть за время <τ> / 2, следовательно, δ = <v1>τ / 2. А так как скорость шара за это время меняется от v1 до 0, то можно считать, что средняя скорость за это время: <v1> = v1 / 2. Таким образом, δ ≈ v1<τ> / 2, и тогда радиус контакта
r = |
Rv1 |
τ |
. |
(4.74) |
2 |
|
|||
|
|
|
|
Теперь для характерного давления при ударе получаем
P ≈ |
2 F |
= |
2mv1 τ |
= 4 |
m |
2 . |
(4.75) |
|
πr |
2 |
πRv1τ 2 |
πR τ |
|||||
|
|
|
|
|
|
|||
В случае не абсолютно упругого (неупругого) удара часть кинетической энергии шаров при соударении переходит в энергию остаточной деформации. Представляет интерес определить энергию остаточной деформации. Для неупругого удара выполняется неравенство
m1v12 + m2v22 > m1u12 + m2u22 . |
(4.76) |
Выполняя преобразование, аналогичные приведенным выше, можно получить:
v1 −v2 > −(u1 −u2 ),
то есть при неупругом ударе шаров относительная скорость их меняет свое направление на противоположное, уменьшаясь при этом по абсолютной величине. Для модулей относительной скорости, можно записать:
v1 −v2 > u1 −u2 .
Для количественной оценки уменьшения относительной скорости вводится коэффициент восстановления.
68
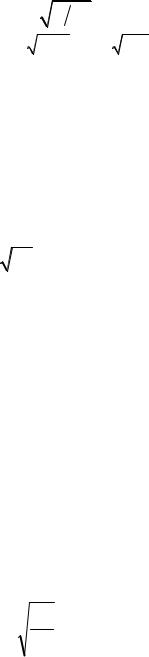
k = |
|
v1 |
−v2 |
|
|
. |
(4.77) |
||
|
|
||||||||
|
|
|
|
|
|
|
|||
|
u |
−u |
2 |
|
|
|
|||
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
В условиях эксперимента коэффициент восстановления можно считать, величиной зависящей только от материала соударяющихся тел; посредством k можно характеризовать упругие свойства того или иного материала.
Для абсолютно упругого удара, как следует из уравнения (4.77), v1 – v2 = u2 и k = 1. Для абсолютно неупругого удара: u1 = u2 и k = 0. Для промежуточного удара, то есть наиболее вероятного удара 0 < k < 1.
Значение k можно определить экспериментально, например, по высоте h, на которую подскакивает шарик, свободно падающий на горизонталь-
ную плиту с высоты H. В этом случае k = |
h H (так как плита неподвиж- |
ная, для нее v2 = u2 = 0, а для шарика v1 = |
2gH , u1 = 2gh ). |
При соударении шаров одинаковой массы, отклоненных на одинаковые углы, нетрудно рассчитать скорости в момент удара, которые будут одинаковые (так как mv 2 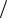 2 = mgh , где h – высота подъема шара). Однако
2 = mgh , где h – высота подъема шара). Однако
проще измерять не высоту подъема, а дугу или угол, на который отклонен шар. Тогда не трудно показать, что для малых углов (α≤100)
h = (1−cosα) = |
α |
2 |
, |
|
|
||
2 |
|
||
где – длина нитей подвеса. |
|
|
|
v =α g . |
|
|
|
Аналогично можно определить и скорость шаров после удара u, измерив величину угла, на который отклонится любой из шаров после удара. Одной пары полученных значений v и u достаточно для определения коэффициента восстановления. Если в формуле (4.77) подставить
v1 = −v2 =v и u1 = −u2 = u , получим k = u / v. Если учесть связь между скоростью шара и углом его отклонения, то выражение для k упростится:
k = u |
= |
α2 |
, |
(4.78) |
v |
|
α1 |
|
|
где α1 – угол отклонения шара до удара; α2 – угол отклонения шара после удара. Уменьшение угла после первого соударения может оказаться весьма малым. Это вызовет трудности в отсчете угла и приведет к большой погрешности результата. Поэтому целесообразно измерить величину угла не после первого соударения, а после 10–15 соударений. В этом случае формула для k должна быть видоизменена следующим образом:
α |
|
k = n αn . |
(4.79) |
1 |
|
69 |
|
Зная коэффициент восстановления, не трудно рассчитать энергию остаточной деформации Еод. Если пренебречь сопротивлением, закон сохранения энергии для удара двух одинаковых шаров запишется так:
mv 2 |
+ |
mv 2 |
= |
mu2 |
+ |
mu2 |
+ 2Eод , |
|
1 |
2 |
1 |
2 |
|||||
2 |
2 |
2 |
2 |
|||||
|
|
|
|
где Еод – энергия остаточной деформации одного шара, относящегося к одному соударению. Учитывая, что k = u v , приходим к соотношению
v , приходим к соотношению
E |
= |
mv 2 |
(1−k ) |
. |
(4.80) |
|
|||||
од |
2 |
|
|||
|
|
|
|
||
Если в результате соударения происходит превращение механической энергии в другие (немеханические) формы энергии, то такой удар называется неупругим. В этом случае выполняется только закон сохранения импульса.
Если после удара оба взаимодействующих тела движутся с одной и той же скоростью, как единое целое, то такой удар носит название абсолютно неупругого. Абсолютно неупругий удар характеризуется тем, что упругие деформации не возникают и кинетическая энергия соударяющихся тел полностью или частично превращается во внутреннюю энергию. После удара столкнувшиеся тела движутся как единое целое. При абсолютно неупругом ударе закон сохранения механической энергии не соблюдается (имеет место закон сохранения суммарной энергии различных видов – механической и внутренней), а выполняется только закон сохранения импульса:
m1v1 + m2v2 = (m1 + m2 )u |
(4.81) |
||
где m1 и m2 массы тел, v1 и v2 – их скорости до удара, |
u – скорость тел |
||
как единого целого после удара. Из (4.81) следует, что |
|
||
u = |
m1v1 + m2v2 |
. |
|
|
|
||
|
m1 + m2 |
|
|
Если векторы v1 и v2 направлены вдоль одной прямой, то вектор
u имеет направление, совпадающее с этой прямой. При центральном ударе соударение может произойти, если:
–шары движутся навстречу друг другу;
–один шар догоняет другой.
Модуль вектора может быть вычислен по следующей формуле:
u = |
|
m1v1 ± m2v2 |
|
, |
(4.82) |
|
m1 + m2 |
||||||
|
|
|
|
|||
где v1 и v2 – модули векторов v1 и v2 , знак «–» соответствует случаю (1), знак «+» – случаю (2).
70

Кинетические энергии системы до удара и после удара равны соответственно:
|
mv 2 |
+ m v 2 |
и EK 2 = |
(m + m |
)u 2 |
|
EK1 = |
1 1 |
2 2 |
1 2 |
|
. |
|
2 |
|
|||||
|
|
2 |
|
|
|
|
Пользуясь этими выражениями, нетрудно получить, что
|
|
|
EK1 − EK 2 |
= |
µ(v1 −v |
2 )2 |
, |
(4.83) |
|
m1m2 |
|
2 |
|
||||
|
|
|
|
|
|
|
||
где µ = |
|
– приведенная масса шаров. |
|
|
|
|||
m + m |
2 |
|
|
|
||||
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кинетической энергии макроскопического движения, равная половине произведения приведенной массы на квадрат относительной скорости.
Описание лабораторной установки
Схема установки приведена на рис. 4.17. Шары 1 и 2 подвешены на проводящих нитях длиной A. Шар 1 с помощью электромагнита, закрепляемого винтом 4, может быть зафиксирован на различных углах бросания α1, в пределах от 15º до 35º на шкале 5. При нажатии на пусковую кнопку электромагнит отключается и отпускает шар 1. Во время удара шары замыкают цепь электронного секундомера 6, с помощью которого производится измерение продолжительности соударения. По шкале 5 производится отсчет угла отскока α2 шара 2.
Для восстановления исходного состояния системы надо отжать кнопку "пуск" (при этом включается электромагнит), прилепить шарик 1 к электромагниту, а затем нажатием кнопки "сброс" обнулить показания табло на секундомере.
При вертикальном положении нитей с шариками (рис. 4.17) они должны быть на одном уровне и слегка касаться друг друга, а их указатели показывать на нули шкалы углов. При захвате магнитом шарика 1, его указатель показывает α1.
Скорость v1 шарика 1 перед самим ударом определяется из закона сохранения энергии m1v12/2 = mgh1, где h1 – изменение высоты центра масс
шарика. Отсюда v1 = 2gh1 . Но h1= – cos α1= |
(1 – cos α1), где α1 – ис- |
ходный угол отклонения шарика и тогда |
|
v1 = 2g (1−cos a1 ) . |
(4.84) |
Аналогично определяется скорость второго шарика u2 сразу после его отскока, то есть по углу его отброса α2.
71

Рис. 4.17
Измерения и обработка результатов измерения
1.Ознакомьтесь с установкой и порядком ее включения.
2.Определите параметры установки, результаты занесите в табл. 4.11.
3.Подготовьте установку к работе. Отведите шарик 1 до его захвата
электромагнитом. Шарик 2 – неподвижен. Определите угол α1. Нажав кнопку «пуск», зафиксируйте по шкале угол максимального отброса α2 второго шарика. По электрическому секундомеру определите время соударения t. Результаты занесите в табл. 4.12. Опыт повторите пять раз.
4.Проведите эксперимент, описанный в пункте 3, для пяти различных углов отклонения α1 первого шарика.
5.По полученным экспериментальным данным определите среднюю силу удара <F>, радиус контактной площадки r, давление p, возникающее при ударе.
6.Отклоните шар на заданный начальный угол α1 и зафиксируйте его электромагнитом. Отключите электромагнит и определите угол, отклонения шара после 10–15 соударений. Операцию повторите пять раз. Рассчитайте среднее значение <∆F>.
7.Опыт по пункту 6 повторите для трех разных начальных углов.
8.Сравните результаты k, полученных из формул (4.77) и (4.79).
9.Для значений α1, при которых определялось время соударения, определите энергию остаточной деформации Еод по формуле (4.80).
10.По полученным данным постройте зависимость Еод(v).
Таблица 4.11
Масса |
∆m, |
Длина |
∆l, |
Радиус |
∆R, |
шара |
кг |
Нити |
м |
шара |
м |
m, кг |
l, м |
R, м |
|||
|
|
|
|
|
|
|
|
72 |
|
|
|
