где N – количество частиц в системе (твердом теле).

Момент импульса системы материальных точек (твердого тела) Lz

относительно оси Z равен алгебраической сумме проекций Lzi всех точек системы на эту ось:

i=1

Момент импульса твердого тела относительно оси вращения Z можно выразить следующим образом:

N

∑mi Ri2 = J z , получаем выражение для момента импульса тела относи-

i=1

тельно оси вращения Z:

Lz = J zω z ,

где Jz – момент инерции твердого тела относительно оси Z.

Закон сохранения момента импульса: момент импульса замкнутой системы материальных точек остается постоянным, то есть L = const .

Лабораторная работа № 2

ИЗУЧЕНИЕ СУХОГО ТРЕНИЯ

Цель работы

Изучение явления сухого трения и экспериментальное определение коэффициентов трения покоя, трения скольжения и трения качения.

Содержание работы

Силы трения возникают не только при перемещении соприкасающихся тел или их частей друг относительно друга (трение скольжения), но также и при попытках вызвать такое скольжение (трение покоя). В случае, если соприкасающиеся тела движутся друг относительно друга, то различают трение скольжения и трение качения.

Трение называется внешним, если силы трения действуют между различными телами, не образующими единое целое (например, трение между покрышкой колеса автомобиля и дорогой). Трение называется внутренним, если силы трения действуют между частями одного и того же тела (например, если силы трения возникают между слоями жидкости или газа, скорости которых различны и непрерывно меняются от слоя к слою). При

45

этом силы трения направлены по касательным к трущимся поверхностям (или слоям), противодействуя их взаимному перемещению.

Трение между поверхностью твердого тела и окружающей его жидкой или газообразной средой, в которой оно движется, а также трение между различными частями такой среды, называется жидким или вязким трением. Трение между поверхностями соприкасающихся твердых тел при отсутствии жидкой или газообразной прослойки между ними называется

сухим.

Остановимся на изучении видов сухого трения более подробно.

Трение покоя

Механизм возникновения силы трения покоя заключается в том, что поверхность даже хорошо отшлифованного тела имеет микроскопические неровности, выступы, трещины, которые препятствуют движению. Взаимное заполнение этих выступов соприкасающимися телами и будет препятствовать их относительному перемещению. Вероятно, что на некоторых участках расстояние между соприкасающимися телами может оказаться порядка радиуса действия молекулярных сил, что приведет к слипанию тел на данных участках, также препятствующему их относительному перемещению. Внедрению микровыступов и частичному слипанию поверхностей способствует сила нормального давления, прижимающая твердые тела друг к другу. Этой силой может служить сила тяжести или ее нормальная составляющая, а также любая другая сила, нормальная поверхности соприкосновения тел.

Если на одно тело не действуют внешние силы вдоль поверхности его соприкосновения с другим телом, то сила трения покоя равна нулю. По мере возрастания величины внешней силы будет возрастать равная и противоположно направленная ей сила трения покоя так, что сумма этих сил будет оставаться равной нулю, и тело будет оставаться в покое. Тело будет покоиться до тех пор, пока прилагаемая к нему внешняя сила не превзойдет по величине максимальной силы трения покоя. Внешняя сила, меньшая максимальной силы трения покоя, вызывает в основном упругие деформации микровыступов и областей, где действуют силы молекулярного сцепления. При достижении определенной величины внешней силы тело придет в движение, трение покоя перейдет в трение скольжения.

Максимальная сила трения покоя, а также сила трения скольжения пропорциональны силе реакции опоры N, численно равной силе нормального давления

где безразмерный коэффициент пропорциональности µ называется коэф-

фициентом трения покоя или соответственно трения скольжения, он зави-

сит от материала поверхностей, их микрогеометрического профиля, а также от других факторов. Выражение (4.19) называется законом Амонтона.

46

то есть коэффициент трения покоя численно равен тангенсу предельного угла наклона α0.

Трение скольжения

Если сила, действующая на тело вдоль поверхности его соприкосновения с другим телом, больше предельного значения силы трения покоя, то тело приобретает ускорение, и сила трения покоя переходит в силу трения скольжения. Сила трения скольжения зависит как от природы и состояния трудящихся поверхностей, так и от относительной скорости тел v. Вначале с возрастанием относительной скорости v величина силы трения скольжения несколько уменьшается, а затем начинает возрастать. В случае, когда состояние поверхностей не изменяется (за счет сглаживания поверхностей, нагрева и т. д.), сила трения скольжения оказывается практически не зависящей от скорости и равной максимальной силе трения покоя.

Трение скольжения возникает в результате пластических деформаций микровыступов и их частичного разрушения. Взаимное проскальзывание тел приводит к уменьшению зацеплений микровыступов и уменьшению слипания поверхностей, в результате чего коэффициент трения скольжения меньше коэффициента трения покоя.

47

Для определения коэффициента трения скольжения поместим на горизонтальную плоскость брусок массой m1 (рис. 4.6). Приведем брусок в движение с помощью груза с массой m2. На основании второго закона Ньютона для каждого из этих тел можно записать уравнения движения, которые имеют вид:

Полагая нить нерастяжимой, нить и блокневесомыми, можем записать:

|a1| = |a2| = а, |F1| = |F2| = F.

Тогда в проекциях на направления x и y и с учетом закона Амонтона

Учитывая, что брусок движется равноускоренно, пройденный им путь будет определяться выражением

где t – время движения бруска.

Решая уравнения (4.26) – (4.29) относительно µ, получим окончательное выражение для искомого коэффициента трения скольжения:

Трение качения

Если цилиндрическое или шарообразное тело катится по плоской или изогнутой поверхности, то между ними возникает сила трения качения. Установлено, что возникновение этой силы обусловлено неупругими деформациями катящегося тела и поверхности. Сопротивление перекатыванию может быть учтено введением момента силы трения качения Мтр.

Опыт показывает, что сопротивление перекатыванию зависит от упругих свойств материалов соприкасающихся тел и от величины прижимающей силы. Для преодоления сопротивления перекатыванию требуется совершать работу, которая переходит в энергию деформации соприкасающихся поверхностей.

Рассмотрим цилиндрическое тело, неподвижно лежащее на горизонтальной плоскости и оказывающее на плоскость давление силой Q (рис. 4.7). В зоне соприкосновения цилиндра с плоскостью возникает местная деформация контактного сжатия на площадке AOB шириной b. Согласно положениям теории упругости напряжения, возникающие в площадке,

48

распределяются по эллиптическому закону. Кривая распределения напряжений имеет симметричный вид, и равнодействующая N этих напряжений совпадает с направлением силы Q.

Рис. 4.7

При перекатывании цилиндра под действием силы P участок АО площадки контакта будет находиться под действием исчезающих деформаций, участок ОВ – под действием нарастающих деформаций. Из–за внутреннего трения в материале нагрузка и разгрузка в нем не совпадают во времени – разгрузка происходит с запаздыванием. Поэтому кривая распределения напряжений в области нарастающих деформаций выше кривой в области исчезающих деформаций. Равнодействующая N напряжений смещена

Величину k называют коэффициентом трения качения.

Цилиндр перекатывается без скольжения под действием момента, создаваемого парой сил – Р и Fтр, где Fтр – сила трения покоя, называемая также силой сцепления

Таким образом, величина силы трения качения Fтр, как и величина равной ей внешней силы P, прикладываемой к цилиндру для его равномерного перекатывания, пропорциональна силе нормального давления Q и обратно пропорциональна радиусу цилиндра r.

В случае, когда сила приложена не в точке С катящегося тела, а на произвольно выбранном расстоянии h, в приведенных соотношениях подставляется h вместо радиуса цилиндра r.

49

Под действием силы Р цилиндр может в одних условиях перекатываться, в других – скользить. Рассмотрим, при каких условиях происходит скольжение, а при каких – качение.

коэффициента трения скольжения µ, поэтому в технике трение скольжения по возможности заменяют трением качения.

Силы трения всегда направлены в сторону, противоположную перемещению, поэтому работа сил трения всегда отрицательна. Движение при наличии сил трения всегда сопровождается диссипацией механической энергии (превращением ее во внутреннюю энергию), поэтому силы трения называются диссипативными.

а значение силы реакции опоры N равно проекции силы тяжести на направление y

Подставив Fk и N из формул (4.34) и (4.35) в выражение (4.33), получим:

50

Описание лабораторной установки

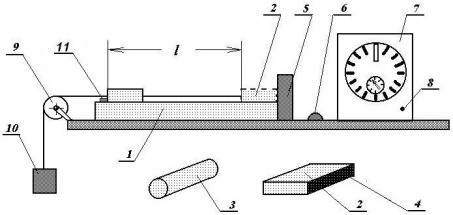
Особенности внешнего трения могут быть изучены с помощью наклонного трибометра, представляющего собой плоскость 1 (рис. 4.9), угол наклона которой к горизонту можно менять.

Рис. 4.9

Исследуемые тела: деревянный брусок 2 и деревянный цилиндр 3; брусок имеет железную вставку 4 для удержания его электромагнитом 5. Тумблером 6 выключается питание электромагнита и одновременно включается электрический секундомер 7. Полный оборот большой стрелки секундомера соответствует одной секунде, малая стрелка отсчитывает целые секунды, то есть число оборотов большой стрелки.

Нажатием кнопки 8 до упора стрелка секундомера устанавливается на нуль. Прикрепив к торцу деревянного бруска нить и перекинув ее через блок 9, с помощью груза 10 можно привести деревянный брусок в движение. Пройдя расстояние l, брусок ударяется о планку 11 и выключает секундомер.

Порядок выполнения работы

Задание 1. Определение коэффициента трения покоя

1.Изучите правила пользования оптическим квадрантом (см. приложение к работе).

2.Установите плоскость 1 трибометра (рис. 4.9) горизонтально.

3.Поставьте на наклонную плоскость деревянный брусок 2.

4.Плавно изменяя угол наклона плоскости, найдите такое предельное значение угла наклона αo , при котором брусок начинает движение.

5.С помощью оптического квадранта измерьте угол наклона плоскости αo. Измерения повторите 3 раза.

6.Данные измерений занесите в табл. 4.3.

51

Задание 2. Определение коэффициента трения скольжения

1.Установите плоскость 1 трибометра горизонтально.

2.Установите стрелки секундомера 7 на нуль, нажав кнопку 8 до упора.

3.Включите цепь электромагнита, поставив тумблер 6 в положение "электромагнит".

4.На плоскость 1 трибометра поставьте деревянный брусок 2 так, чтобы он удерживался электромагнитом 5 (металлическая вставка 4 должна быть обращена к электромагниту).

5.Нить с чашкой и грузом прикрепите к бруску и перекиньте через блок.

6.Переключите тумблер 6 в положение "секундомер".

7.По секундомеру 7 определите время движения бруска t до момента удара бруска о планку 11. Измерения повторите 10 раз.

8.Линейкой измерьте путь l, пройденный бруском.

9.Данные измерений занесите в табл. 4.4.

Задание 3. Определение коэффициента трения качения

1.Установитеплоскость1 трибометрагоризонтально.

2.Штангенциркулем измерьтедиаметрd основаниядеревянногоцилиндра3.

3.Положите цилиндр на плоскость 1 трибометра. Плавно изменяя наклон

плоскости, найдите такое предельное значение угла наклона α0, при котором цилиндр начинает движение.

4.С помощью оптического квадранта измерьте угол наклона α0 . Измерения повторите3 раза.

5.Данныеизмеренийзанеситевтабл. 4.5.

52

Обработка результатов измерений

Расчет коэффициента трения покоя:

–найдите среднее значение угла наклона < α0 >;

–поформуле(4.23) вычислитезначениекоэффициентатренияпокоя µo;

–результат занесите в табл. 4.3.

Расчет коэффициента трения скольжения:

–найдите среднее значение времени движения бруска < t >;

–измерьтепутьl, пройденныйбруском;

–по формуле (4.30) вычислите значение коэффициента трения скольжения µ (массы бруска m1 и груза m2 приведены на лабораторном столе).

–результаты занесите в табл. 4.4.

Расчет коэффициента трения качения:

–найдите среднее значение предельного угла наклона <α0 > ;

–измерьте в трех местах штангенциркулем диаметр цилиндра;

–вычислите среднее значение диаметра < d >;

–определите радиус основания цилиндра r;

–по формуле (4.36) вычислите значение коэффициента трения качения k;

–вычислите отношение k/r;

–результаты вычислений занесите в табл. 4.5;

–сравните полученные значения µ0, µ и k/r.

Контрольные вопросы

1.Что называется внешним (сухим) трением? Дайте характеристики различных видов сухого трения.

2.От каких факторов зависит модуль силы трения? Как направлена сила трения?

3.Каков механизм возникновения трения покоя? Трения скольжения? Трения качения?

4.Сформулируйте и запишите закон Амонтона.

5.Какие силы действуют на цилиндр при его качении по горизонтальной поверхности? По наклонной плоскости?

53