- •1.9. Геометрия
- •2.2.2. Взаимное расположение прямых в пространстве
- •2.2.3. Взаимное расположение прямой и плоскости
- •2.3. Кривые второго порядка
- •2.3.1. Эллипс
- •2А Рис. 11, а
- •2.3.2. Гипербола
- •2.3.3. Парабола
- •2.4. Поверхности второго порядка
- •2.4.1. Центральные поверхности
- •2.4.2. Параболоиды
- •2.4.3. Цилиндры
- •3. Основы векторной алгебры
- •3.1. Скалярные и векторные величины
- •3.2. Линейные операции над векторами
- •3.3. Проекции вектора на ось
- •3.4. Направляющие косинусы вектора. Модуль вектора
- •3.5. Скалярное произведение
- •3.6. Векторное произведение
- •3.7. Смешанное произведение векторов
- •3.8. Операции над векторами, заданными в координатной форме
2.3.3. Парабола

Определение. Параболой называется геометрическое место точек, равноудаленных от данной точки F, называемой фокусом, и от данной прямой (АВ), называемой директрисой (предполагается, что эта прямая не проходит через фокус).
Каноническое уравнение параболы
![]() ,
,
где
![]() – фокальный параметр параболы, равный
расстоянию от фокуса
до директрисы, 0
– центр па-
– фокальный параметр параболы, равный
расстоянию от фокуса
до директрисы, 0
– центр па-
раболы,
отрезок
![]() – фокальный радиус точкиМ
(рис. 14,
а).
– фокальный радиус точкиМ
(рис. 14,
а).
П арабола,
заданная уравнением
арабола,
заданная уравнением![]() ,
симметрична относительно оси
,
симметрична относительно оси![]() и простирается в бесконечность.
и простирается в бесконечность.
Эксцентриситет
всякой параболы равен единице
![]() .
.
Если
ось
![]() – ось параболы,О
– ее вершина, точка
– ось параболы,О
– ее вершина, точка
 – фокус, то ее уравнение:
– фокус, то ее уравнение:![]() (рис. 14,б).
(рис. 14,б).
Центр
параболы в точке
![]()


![]()
![]()
Пример. Уравнение кривой записать в каноническом виде и построить график.
1.
![]() 2.
2.![]()
Решение.
|
1.
|
2.
|
|
|
|
2.4. Поверхности второго порядка
2.4.1. Центральные поверхности
|
Эллипсоид |
Конус |
|
Рис. 1
|
Рис. 3
вершина в начале координат |
|
Гиперболоид однополостной |
Гиперболоид двухполостной |
|
Рис. 2
|
Рис. 4
|
2.4.2. Параболоиды
|
Эллиптический параболоид |
Гиперболический параболоид |
|
Рис. 5
|
Рис. 6
|
2.4.3. Цилиндры
Уравнение
вида
![]() в пространстве определяет цилиндрическую
поверхность, образующая которой
параллельна оси
в пространстве определяет цилиндрическую
поверхность, образующая которой
параллельна оси![]() .
.
|
Эллиптический цилиндр |
Параболический цилиндр |
|
Рис. 7
Если
|
Рис. 8
|
Гиперболический цилиндр
Рис. 9

3. Основы векторной алгебры
3.1. Скалярные и векторные величины
Скалярными
называются величины, которые могут быть
охарактеризованы числами (например,
длина, площадь, объем, масса, плотность,
работа и др.). Векторными
называются величины, для полной
характеристики которых требуется
указания числа и направления в пространстве
(например, скорость, ускорение, сила и
др.). Вектором
называется направленный
отрезок АВ,
у которого точки А
и В
являются соответственно началом и
концом. Вектор обозначается АВ
= а,
его длина (модуль или длина вектора)
обозначается
![]() Вектор, у которого начало совпадает с
концом, называетсянуль-вектором.
Длина нуль-вектора равна нулю.
Вектор, у которого начало совпадает с
концом, называетсянуль-вектором.
Длина нуль-вектора равна нулю.
Векторы называются коллинеарными, если они параллельны одной и той же прямой или если они расположены на параллельных прямых. Следовательно, направления коллинеарных векторов либо совпадают, либо противоположны.
Н а
рис. 5 векторыа,
в,
с
и d,
е
соответственно коллинеарны, причем, а
и в
одинаково направлены, векторы а,
с;
в,
с;
d,
е
– противоположно направлены.
а
рис. 5 векторыа,
в,
с
и d,
е
соответственно коллинеарны, причем, а
и в
одинаково направлены, векторы а,
с;
в,
с;
d,
е
– противоположно направлены.
Рис. 16
Нуль-вектор считается коллинеарным любому вектору. Два (ненулевых) вектора а и в равны, если они одинаково направлены и имеют одинаковую длину. Это записывается так: а = в.
Если длины двух векторов равны, но они противоположно направлены, то такие векторы называются противоположными. Вектор, противоположный вектору АВ = а, записывается так: ВА = – а.
Если векторы лежат в одной и той же плоскости, то они называются компланарными. Два вектора всегда компланарны. На рис. 16 векторы а, в, с, d, е являются компланарными.
Единичным называется вектор, длина которого равна единице; единичный вектор, направление которого совпадает с направлением вектора а, обозначается ао и называется ортом этого направления. Орты, имеющие направление прямоугольных координатных осей Ох, Оу, Оz (в сторону их положительного направления) обозначаются i, j, k (рис. 17 и 20).
Р адиус-вектором
точкиА(х,
у,
z)
называется такой вектор r,
начало которого совпадает с началом
координат, точкой О,
а конец расположен в точке А
(рис. 17). Если радиус-вектор r
точки А
делит отрезок А1А2
адиус-вектором
точкиА(х,
у,
z)
называется такой вектор r,
начало которого совпадает с началом
координат, точкой О,
а конец расположен в точке А
(рис. 17). Если радиус-вектор r
точки А
делит отрезок А1А2
в
отношении
 ,
иr1
и r2
– радиус-векторы точек А1
и А2,
то справедлива формула
,
иr1
и r2
– радиус-векторы точек А1
и А2,
то справедлива формула
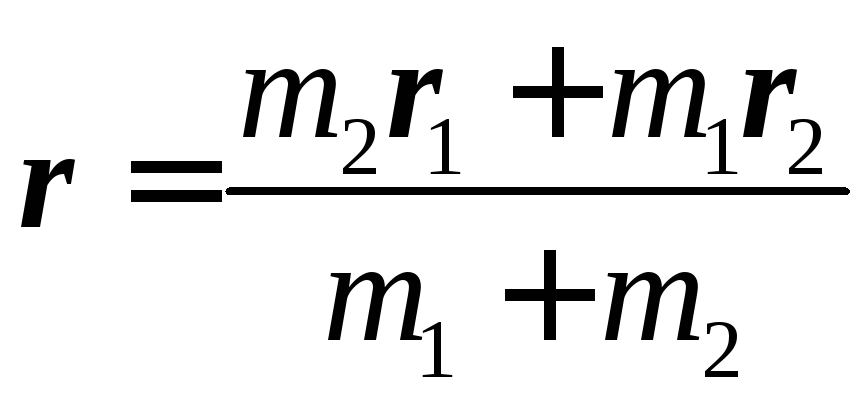 .
.
Следовательно, координаты точки А можно найти по формулам:



В частности, координаты середины отрезка А1А2 соответственно равны:
![]()
![]()
![]()
В
Рис. 18

Итак, в дальнейшем будем иметь дело со свободными векторами, т. е. векторами, определенными с точностью до параллельного переноса.

 парабола,
вершина
которой в точке
парабола,
вершина
которой в точке