
- •1.9. Геометрия
- •2.2.2. Взаимное расположение прямых в пространстве
- •2.2.3. Взаимное расположение прямой и плоскости
- •2.3. Кривые второго порядка
- •2.3.1. Эллипс
- •2А Рис. 11, а
- •2.3.2. Гипербола
- •2.3.3. Парабола
- •2.4. Поверхности второго порядка
- •2.4.1. Центральные поверхности
- •2.4.2. Параболоиды
- •2.4.3. Цилиндры
- •3. Основы векторной алгебры
- •3.1. Скалярные и векторные величины
- •3.2. Линейные операции над векторами
- •3.3. Проекции вектора на ось
- •3.4. Направляющие косинусы вектора. Модуль вектора
- •3.5. Скалярное произведение
- •3.6. Векторное произведение
- •3.7. Смешанное произведение векторов
- •3.8. Операции над векторами, заданными в координатной форме
1.9. Геометрия
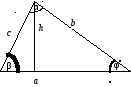
Треугольник
![]()
![]()
Теорема
синусов:

Т еорема
косинусов:
еорема
косинусов:![]()
Окружность, круг
Длина
окружности:
![]()
Длина
дуги АВ:

Площадь
круга:
![]()

Другие фигуры
Сфера и шар
![]() –площадь
сферы
–площадь
сферы
![]()
 –объем
шара
–объем
шара
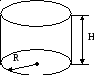
Цилиндр
![]() –площадь
боковой поверхности
–площадь
боковой поверхности
![]() –объем
цилиндра.
–объем
цилиндра.

Конус
![]() –площадь
боковой поверхности;
–площадь
боковой поверхности;
![]() –объем
конуса.
–объем
конуса.
2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
2.1. Прямая на плоскости. Плоскость
2.1.1. РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЙ
|
Прямая на плоскости |
Плоскость |
|
у М2(х2,у2)
М1(х1,у1)
b
α
0
х a М0(х0,у0)
Рис. 5
где
|
Рис. 6 |
|
1) Общее уравнение | |
|
|
|
|
2) Уравнение в отрезках | |
|
|
|
|
3)
Уравнение прямой через заданную
точку
|
Уравнение
плоскости через заданную точку
|
|
4)
Уравнение прямой, проходящей через
две заданные точки
|
Уравнение
плоскости, проходящей через три
заданные точки
|
|
5)
Расстояние от заданной
точки
| |
|
до прямой |
до плоскости |
|
|
М0(х0,у0,z0)
d
α
|
|
2.1.2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ | |
|
прямых |
плоскостей |
|
Так
как
|
|
|
Условие параллельности прямых
|
Условие параллельности плоскостей
|
|
Условие перпендикулярности прямых
|
Условие перпендикулярности плоскостей
|
|
Частные случаи расположения | |
|
прямых на плоскости |
плоскостей |
|
Свободный
член
|
Свободный
член
|
|
Рис. 7 |
Если в уравнении плоскости отсутствуют переменные (коэффициенты при этих переменных равны нулю), то данная плоскость расположена параллельно той оси координат или той координатной плоскости, в которых эти переменные присутствуют. (Что «отсутствует» – тому и параллельна): |
|
прямая
параллельна оси
|
● уравнение
|
|
прямая
параллельна оси
|
● уравнение
|
|
Уравнения осей координат на плоскости:
|
Уравнения координатных плоскостей:
|
|
2.2. Прямая в пространстве
2.2.1. РАЗЛИЧНЫЕ УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ
| |
|
Рис. 8 |
Это
общее
уравнение прямой
АВ,
как линии
пересечения двух плоскостей α и β.
Векторы
●
Это каноническое уравнение прямой. |
Если
обозначить
![]()
![]()
![]() где
где![]() – параметр, то получимпараметрическое
уравнение
прямой ●
– параметр, то получимпараметрическое
уравнение
прямой ●
 (3)
(3)

Точки
![]() и
и![]()
![]()
В этом случае уравнение (2) можно записать в следующем виде:
●
 (4)
(4)
Полученное
уравнение прямой (8) называется уравнением
прямой, проходящей через две заданные
точки
![]() и
и
![]() .
.
Замечание.
Нормальные векторы
![]() и
и![]() одновременно перпендикулярны направляющему
вектору
одновременно перпендикулярны направляющему
вектору![]() .
Следовательно,
.
Следовательно,![]() коллинеарен вектору, равному векторному
произведению
коллинеарен вектору, равному векторному
произведению![]() и
и![]() .
Принимая коэффициент пропорциональности
одноименных координатных коллинеарных
векторов равным единице, получим формулу
для нахождения координат направляющего
вектора прямой через координаты
нормальных векторов плоскостей,
пересекающихся по этой прямой:
.
Принимая коэффициент пропорциональности
одноименных координатных коллинеарных
векторов равным единице, получим формулу
для нахождения координат направляющего
вектора прямой через координаты
нормальных векторов плоскостей,
пересекающихся по этой прямой:
 .
.













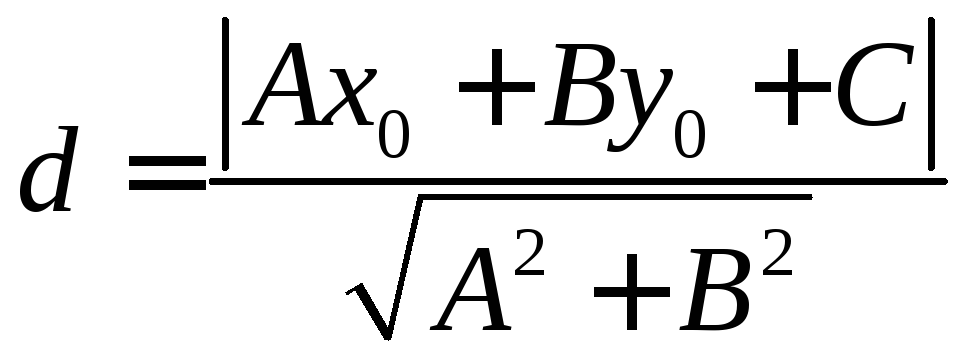




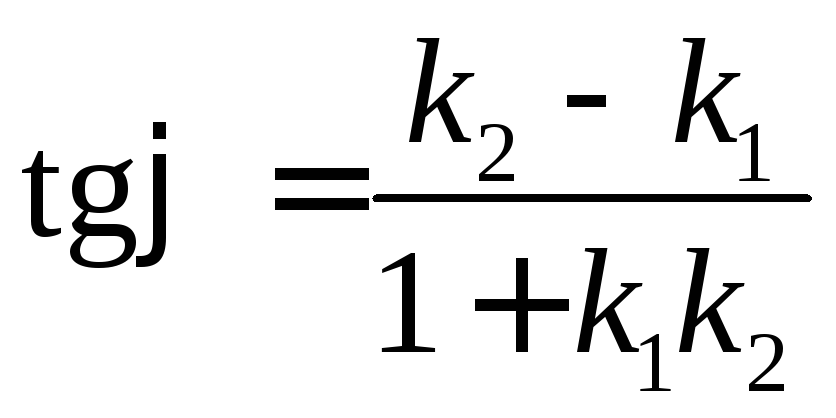

 то
то






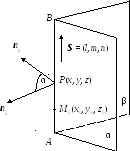
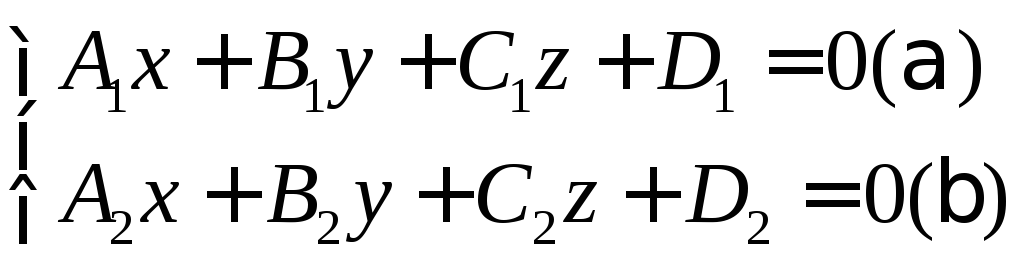 (1)
(1)