
- •4. Матрицы. Системы линейных уравнений
- •4.1. Числовые матрицы Основные понятия и определения
- •● Минором элемента называется определитель (n–1)-гопорядка, образованный из определителя n-го порядка вычеркиванием I-ой строки и j-го столбца и обозначается .
- •4.2. Свойства определителей
- •4.3. Действия над матрицами
- •4.3.1. Линейные действия над матрицами. Их свойства
- •Свойства линейных операций над матрицами
- •Свойства умножения матриц
- •4.5.2. Правило крамера
- •4.5.3. Решение систем линейных уравнений с помощью обратной матрицы
- •4.5.4. Метод последовательного исключения неизвестных
- •4.5.5. Система линейных однородных уравнений
- •4.6. Собственные числа и собственные векторы матрицы
- •5. Начала математического анализа
- •5.1. Понятие функции
- •5.2. Некоторые классы функций
- •5.3. Основные элементарные функции
- •5.4. Графики некоторых функций
- •5.5. Последовательности и их пределы
- •Основные теоремы о пределах последовательностей
- •5.6. Понятие предела функции
- •Основные теоремы о пределах
- •5.7. Бесконечно малые и бесконечно большие величины
- •5.8. Виды неопределенности. Способы устранения неопределенности
Основные теоремы о пределах последовательностей
1. Последовательность может иметь только один предел.
2. Последовательность, имеющая конечный предел, ограниченная; последовательность, имеющая бесконечный предел, неограниченная.
3.
Необходимый
и достаточный признак существования
предела последовательности.
Для того, чтобы последовательность
![]() имела предел, необходимо и достаточно,
чтобы при задании любого как угодно
малого положительного числа
имела предел, необходимо и достаточно,
чтобы при задании любого как угодно
малого положительного числа![]() можно было указать такой ее член
можно было указать такой ее член![]() ,
что любые два члена, стоящие после
,
что любые два члена, стоящие после![]() ,
будут отличаться друг от друга на число,
меньшее
,
будут отличаться друг от друга на число,
меньшее![]() ,
т. е.
,
т. е.
![]() при
при
![]() и
и![]() .
.
5.6. Понятие предела функции
● Функция
![]() при
при![]() имеет предел
А:
имеет предел
А:
![]() ,
если при приближении
,
если при приближении![]() к
к![]() соответствующие значения функции
соответствующие значения функции![]() подходят как угодно близко к числуА.
При значениях
подходят как угодно близко к числуА.
При значениях
![]() функция может не принимать значениеА
и вообще может быть не определена.
функция может не принимать значениеА
и вообще может быть не определена.
Точная
формулировка.
![]() ,
если задав произвольное как угодно
малое
,
если задав произвольное как угодно
малое![]() ,
можно указать такое число
,
можно указать такое число![]() ,
что при любых значени-
яхх
в промежутке
,
что при любых значени-
яхх
в промежутке
![]() (кроме, может быть, значения
(кроме, может быть, значения![]() )
соответствующие значения
)
соответствующие значения![]() будут находиться в промежутке
будут находиться в промежутке![]() ,
т. е. как только
,
т. е. как только![]() ,
так
,
так![]() .
.
Признак
Коши. Для
того чтобы функция
![]() имела предел при
имела предел при![]() ,
необходимо и достаточно, чтобы для любых
двух значений аргумента
,
необходимо и достаточно, чтобы для любых
двух значений аргумента![]() и
и![]() из области задания функции и достаточно
близких к
из области задания функции и достаточно
близких к![]() ,
соответствующие значения функции
,
соответствующие значения функции![]() и
и![]() были сколь угодно близки между собой.
Из формулировки теоремы следует, что
как только
были сколь угодно близки между собой.
Из формулировки теоремы следует, что
как только![]() и
и![]() так выполняется условие
так выполняется условие![]() .
.
Основные теоремы о пределах
1)
Предел постоянной величины С
равен этой величине:
![]() .
.
2)
Если
![]() и
и![]() – числа, то
– числа, то
![]()
3)
![]()
4)
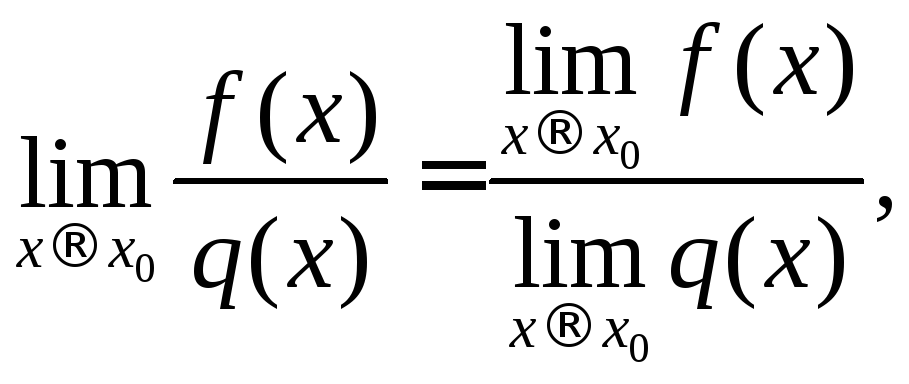 если
если![]()
5)
![]()
6) Монотонная ограниченная функция имеет конечный предел при
любом значении х.
7)
Если
![]() и
и![]() и
и![]() ,
,
то
![]() .
.
Следствие. Чтобы вычислить предел, нужно заменить переменную величину ее предельным значением.
Примеры.
•

•

5.7. Бесконечно малые и бесконечно большие величины
● Переменная
величина α называется бесконечно
малой при
![]() если
если![]() Обозначение бесконечно малой:
Обозначение бесконечно малой:![]()
● Переменная
величина β называется бесконечно
большой при
![]() если
если![]() Обозначение бесконечно большой:
Обозначение бесконечно большой:![]()
● Величина,
обратная бесконечно большой, является
бесконечно малой. Следовательно, если
![]() то
то
![]()
![]()
![]()
![]()


Если
![]() и
и![]() – бесконечно малые величины при
– бесконечно малые величины при![]() и
и то они называютсяэквивалентными
и обозначаются так:
то они называютсяэквивалентными
и обозначаются так:
![]() при
при
![]()
|
Эквивалентные
бесконечно малые при
| |||||
|
|
|
|
|
|
|
● Если
![]() и
и![]() – бесконечно большие величины при
– бесконечно большие величины при![]() или
или![]() и
и то они называютсяэквивалентными
и обозначаются так:
то они называютсяэквивалентными
и обозначаются так:
![]() при
при![]()
![]() .
.
Замечания.
1)
Многочлен n-ой
степени
![]()
![]() при
при![]() является бесконечно большой величиной
эквивалентной старшей степени с
соответствующим коэффициентом:
является бесконечно большой величиной
эквивалентной старшей степени с
соответствующим коэффициентом:
 при
при
![]() .
.
2)
Если
![]() –const,
то
–const,
то

3)
Если
![]() –const,
то
–const,
то

Первый
замечательный предел:
Второй
замечательный предел:
![]()
![]()
5.8. Виды неопределенности. Способы устранения неопределенности
|
|
|
|
|
|
|
|
|
|
|
№ п/п |
Вид неопределенности |
Способы устранения неопределенности |
|
1 |
|
1. Разделить на старшую степень неизвестного в знаменателе. 2. Числитель и знаменатель заменить соответственно на эквивалентные б/б величины.
3.
Правило Лопиталя:
|
|
2 |
|
1.
Числитель и знаменатель разделить
на
2.
Правило Лопиталя:
3. В произведении и частном одну б/м величину можно заменить на другую, ей эквивалентную |
|
3 |
|
1.
2.
|
|
4 |
|
Второй замечательный предел:
|
|
5 |
|
Далее
надо устранить полученную неопределенность
|
|
6 |
|
Обозначим
В зависимости от полученного вида неопределенности применяют соответствующий метод устранения новой неопределенности (см. п. 5) |
Примеры. Вычислить следующие пределы.
1)
 при
при
2)
 при
при![]()

3)


4)


5)

6)


7)
![]()
 получим:
получим:
![]()
![]()
Итак,
![]()




 привести дроби к общему знаменателю
и устранить полученную при этом
неопределенность
привести дроби к общему знаменателю
и устранить полученную при этом
неопределенность

