Матан
.pdf
Билет №1
1) Частные производные первого порядка. Геометрический смысл.
Рассмотрим функцию 
. Пусть независимая
переменная у приняла постоянное значение 
, а переменная 
изменяется. Тогда из функции двух переменных получим функцию
одной независимой переменной 
.
Ее графиком является линия пересечения поверхности 
и плоскости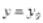 
.
Поскольку 
является функцией одной переменной, ее производная 
в точке 
вычисляется по формуле
2) Признаки сравнения сходимости рядов.
Признаки сравнения рядов
Даны два ряда |
и |
− такие, что |
для всех n. Тогда |
||
справедливы следующие признаки: |
|
||||
ï |
Если |
сходится, то |
также сходится; |
|
|
ï |
Если |
расходится, то |
также расходится. |
||
Предельные признаки сравнения рядов
Пусть даны два ряда 
и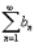 
, у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки:
•Если 
, то оба ряда 
и 
либо сходятся, либо расходятся;
• Если |
, то ряд |
сходится, если сходится ряд |
; |
• Если |
, то ряд |
расходится, если расходится |
ряд .
Так называемый обобщенный гармонический ряд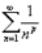 
сходится при p > 1 и
расходится при 0 < p ≤ 1.
Билет №2
1) ДифференцированиеФНП. Необходимые условия дифференцирования. Полный дифференциал.
Пусть функция u = f(x1, x2, … , xn) определена в некоторой окрестности точки a = (a1, a2, … , an) .
Определение 1. Функция u = f(x1, x2, … , xn)
называется дифференцируемой в точке a = (a1, a2, … , an) , если ее полное приращение
можно представить в виде
где Ak — некоторые числа, не зависящие от |
xk ( k = 1,2, … ,n ), αk — |
||
функции |
x1, … , |
xn , бесконечно малые при x1 → 0, … , xn → 0 |
|
и равные нулю при |
x1 = 0, … , xn = 0 . |
|
|
Если функция u = f(x1, x2, … , xn) дифференцируема в точке a = |
|||
(a1, a2, |
… , an) , то линейная относительно |
x1, … , xn часть ее |
|
приращения называется дифференциалом (или полным дифференциалом) функции u в точке a .
Таким образом
Если функция u = f(x1, x2, … , xn) дифференцируема в точке a , то в этой точке существуют частные производные по каждому аргументу.
Теорема: полный дифференциал равен сумме попарных произведений частных производных на дифференциал соответствующих переменных.
2) Признак Даламбера.
Если в ряде с положительными
членами 
отношение 
-го члена ряда к 
-му при 
имеет конечный предел 
,
т.е. 
, то:
-ряд сходится в случае 
,
-ряд расходится в случае 
.
В случаях, когда предел не существует или он равен единице, ответа на вопрос о сходимости или расходимости числового ряда теорема не дает. Необходимо провести дополнительное исследование.
Билет №3
1) Касательная к плоскости и нормаль к поверхности.
Пусть поверхность задана в неявном виде: F(x,y,z)=0 и пусть точка M0(x0,y0,z0) принадлежит данной поверхности. Тогда уравнение касательной плоскости к этой поверхности в точке M0 таково:
F′x(M0) (x−x0)+F′y(M0) (y−y0)+F′z(M0) (z−z0)=0
Уравнение нормали имеет вид: (x−x0)/F′x(M0)=(y−y0)/F′y(M0)=(z−z0)/F′z(M0)
Если же уравнение поверхности задано в явном виде z=f(x,y), то уравнение касательной плоскости имеет вид:
f′x(x0,y0) (x−x0)+f′y(x0,y0) (y−y0)−(z−z0)=0
Уравнение нормали в случае явного задания поверхности таково: (x−x0)/f′x(x0,y0)=(y−y0)/f′y(x0,y0)=(z−z0)/−1
2) Радикальный признак Коши.
Если для ряда 
, ип ≥ 0, существует предел
то при l < 1 ряд 
сходится, а при l > 1 расходится.
Билет №4
1) Достаточное условие дифференцируемостиФНП.
Для того чтобы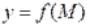 
, определенная в област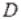и 
и
непрерывная в точке 
была дифференцируемав этой точке, достаточно, чтобы эта функция имела непрерывные частные
производные 
в некоторой окрестности 
, и эти частные
производные были непрерывны в точке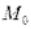 
.
2) Интегральный признак Коши сходимости рядов.
Пусть f (x) является непрерывной, положительной и монотонно убывающей функцией на промежутке [1, +∞). Тогда ряд
сходится, если сходится несобственный интеграл |
, и расходится, |
|
если |
. |
|
Билет №5
1) Достаточное условие экстремума функции двух переменных.
Пусть в некоторой области, содержащей
точку 
функция 
имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме
того, точка 
является критической точкой функции 
, т.е.
,
тогда при 
:
1) 
имеет максимум, если дискриминант 
и 
,
где |
|
|
; |
2) |
имеет минимум, если |
|
|
дискриминант |
и |
; |
|
3) |
не имеет ни минимума, ни максимума, если |
||
дискриминант |
; |
|
|
4) если |
|
, то экстремум может быть, а может и не быть (требуется |
|
дополнительное исследование). |
|
||
2) Признак Лейбница сходимости рядов.
Знакочередующийсяряд
сходится, если выполняются оба условия:
1. 
для всех 
2. 
Билет №6
1) Условный экстремум. Функция Лагранжа. Необходимое условие
условного экстремума.
Точка М 0 (х0 , у0 ) называется точкой максимума функции z = f (x, y), если f (x o , yo) > f (x, y) для всех точек (х, у) из некоторой окрестности точки М 0.
Точка М 0 (х0 , у0 ) называется точкой минимума функции z = f (x, y), если f (x o , yo) < f (x, y) для всех точек (х, у) из некоторой окрестности точки М 0.
(необходимое условие экстремума функции двух переменных). Если
функция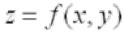 
достигает экстремума при 
,
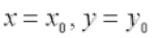то каждая частная производная первого порядка от 
или обращается в нуль при этих значениях аргументов, или не существует.
2) Абсолютная сходимость числовых рядов. Свойства.
Сходящиеся ряды, для которых ряды, составленные из абсолютных величин их членов, также сходятся. Такие ряды называются абсолютно
сходящимися рядами.
пусть для некоторого ряда
выполнено условие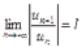 
. Тогда:
1)если 
, то ряд сходится абсолютно,
2)если 
, то ряд расходится.
Билет №7
1) Достаточное условие условного минимума или максимума. Уже было в билете №5.
2) Условно сходящиеся ряды. Теорема Риммена.
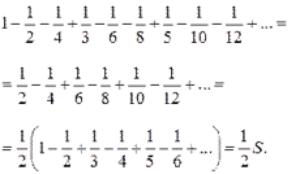
(Риман). Если ряд с действительнымичленами условно
сходится, то, каково бы ни было действительное число s, можно так переставить члены этого ряда , что сумма получившегося ряда будет равна s.
Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Билет №8
1) Неявные функции. Теорема о разрешимости неявной функции. Производная функции, заданной неявно.
Если независимая переменная 
и функция 
связаны уравнением вида 
, которое не разрешено относительно 
, то функция 
называется неявной функцией переменной 
.
Пример производной функции, заданной неявно:
2) Равномерно сходящиеся ряды. Теорема непрерывности суммы равномерно сходящегося ряда.
Если члены функциональногоряда - непрерывные функции, и этот ряд равномерно сходится на отрезке, то сумма этого ряда непрерывна на этом отрезке.
Билет №9
1) Дифференцированиесложной ФНП.
Если u = ƒ(х;у) — дифференцируемаяв точке М(х;у) є D функция и х = x(t) и у = y(t) — дифференцируемыефункции независимой переменной t, то производная сложной функции u(t) = f(x(t);y(t)) вычисляется по формуле
(ошибка, dy/dt)
2) Равномерно сходящиеся ряды. Теорема о почленном интегрировании равномерно расходящемся ряде.
Если члены ряда 
- непрерывные на отрезке [a,b] функции и ряд сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке [a,b].
Равномерно сходящийся на отрезке [a,b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку [a,b] , сходится к интегралу от суммы ряда по этому отрезку.
Билет №10
1) Инвариантность формы 1-го дифференциала для ФНП.
Дифференциал функции z=f(x,y) сохраняет один и тот же вид независимо от того, являются ли ее аргументы u и v независимыми переменными или функциями
2) Равномерно сходящиеся ряды. Теорема о почленном дифференцированииряда.
Если члены ряда 
сходящегося на отрезке [a,b] представляют собой непрерывные функции, имеющие непрерывные производные, и
ряд, составленный из этих производных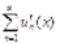 
сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
3)