Матан
.pdf
Билет №11
1) Формула Тейлора для функции многих переменных.
В точке (0;0):
2) Признак равномерной сходимости ряда Вейерштрасса.
Если для функциональногоряда 
можно указать такой
сходящийся числовой ряд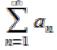 
, что для всех n>n0 и для всех X Е, выполняется условие |un(x)|<an, то ряд сходится абсолютно и
равномерно на множестве Е.
Билет №12
1) Вычисление двойного интеграла сведением к повторному.
с областью «D»
Выражение вида называется повторным
интегралом от функции 
по области 
.
2) Степенные ряды. Радиус сходимости.
Ряд, членами которого являются степенные функции аргумента x,
называется степенным рядом :
Радиусом сходимости степенного ряда |
называется |
||
такое число R, при котором ряд сходится, если |
, и |
||
расходится, если |
. |
. |
|
|
|
Билет №13 |
|
1) Вычисление тройного интеграла сведением к повторному.
Почти то же самое, что и для двойного интеграла.
2) Ряд Тейлора-Маклорена. Достаточное условие сходимости ряда Тейлора-Маклорена.
,
который называется рядом Тейлора для функции
в окрестности точки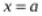
.
Частным случаем ряда Тейлора является ряд Маклорена при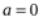
:
+ Остаток ряда Тейлора (Маклорена)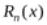 
.
Для того чтобы ряд Тейлора,, имел своей суммой функцию, т.е., необходимо и достаточно, чтобы для всех существовал предел, где− остаток ряда Тейлора.
Достаточное условие:
Если на отрезке 
все производные функции по модулю ограничены одним числом, 
, то f(x) разлагается в ряд Тейлора, который сходится к f(x) на отрезке
Билет №14
1) Замена переменных в тройном интеграле. Цилиндрическая и сферическая система координат.
Тройной интеграл в цилиндрическихкоординатах:
Якобиан равен « r ».
Тройной интеграл в сферических координатах:
Якобиан равен sinѲ
2) Ряд Тейлора-Маклорена для , cos(x), sin(x) с центром в
Билет №15
1) Криволинейный интеграл 1-го и 2-го рода. Формула Грина.
Криволинейный интеграл 1-го рода:
Если кривая l задана уравнением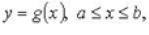 
то
Если кривая l задана параметрически 
то
Криволинейныйинтеграл 2-го рода:
Кривая l задана уравнением y = f(x), x изменяется от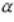 
до 
:
Формула Грина:
Если векторная функция a=ax(x,y)i+ ay(x,y)jнепрерывна вместе со своими производными 
и 
в замкнутой
области 
, то:
2)
Билет №16
1) Поверхностный интеграл 1-го рода. Формула площади поверхности, заданной в параметрическом виде.
Поверхность S задана параметрически:
где 
Площадь поверхности S выражается с помощью поверхностного интеграла в виде
Если поверхность S задана уравнением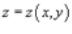 
, где z (x,y) − дифференцируемаяфункция в области D (x,y), то поверхностный интеграл находится по формуле
Если поверхность S состоит из нескольких частей Si, то использовать сумму этих частей.
2) Вычисление ряда Тейлора-Маклорена для y = tg(x) (до третьего порядка включительно)
для всех |
, где |
— Числа Бернулли. |
Билет №17
1) Поверхностный интеграл 2-го рода и его свойства.
Поверхностный интеграл второго рода от векторного поля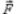 
по ориентированнойповерхности S (или поток векторного поля 
через поверхность S)
При замене рассматриваемойстороны поверхности на противоположную поверхностныйинтеграл 2-го рода меняет знак
2) Ряд Фурье по системе тригонометричскихфункций на [ -π ; π ].
Билет №18
1) Формула Стокса.
2) Условие минимальности уклонения
Билет №19
1) Теорема Остроградского-Гаусса.
где через
обозначена дивергенция векторного поля 
(она обозначается также символом 
).
2) Неравенство Бесселя, равенство Парсеваля.
Неравенство Бесселя
Рассмотрим кусочно непрерывную функцию f (x), заданную в интервале [− π, π]. Ее разложение в ряд Фурье имеет вид
В неравенстве Бесселя устанавливается, что
Отсюда следует, что ряд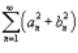 
сходится.
Равенство Парсеваля
Если f (x) является квадратично интегрируемой функцией в интервале [− π, π], так что выполняется соотношение
то неравенство Бесселя становится равенством. В этом случае справедлива формула Парсеваля:
Билет №20
1) Ротор векторного поля. Формула Стокса в векторной форме.
Ротор - векторный дифференциальныйоператор над векторным полем .
Где «» - Едини́чный ве́ктор или орт
Формула Стокса:
2) Условие сходимости Дирихле ряда Фурье.
Пусть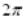 
-периодическая функция 
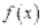удовлетворяет двум условиям:
1. 
кусочно-непрерывна на отрезке 
;
2. 
кусочно-монотонна на отрезке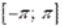 
.
Тогда соответствующий функции 
ряд Фурье сходится на этом отрезке и при этом:
1) в точках непрерывности функции сумма ряда |
совпадает |
|
с самой функцией, т.е. |
; |
|
2) в каждой точке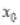 
разрыва функции сумма ряда равна
среднему арифметическому пределов функции 
слева и справа, т.е.
.
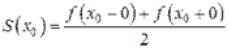Билет №21
1) Соленоидальные векторные поля. Условия соленоидальности.
Векторное поле называется соленоидальнымили вихревым, если через любую замкнутую поверхность S его поток равен нулю:
Для того, чтобы непрерывно дифференцируемое векторное
поле 
было соленоидальным необходимо и достаточно, чтобы оно имело векторный потенциал.
‰ Достаточность. Пусть |
имеет векторный потенциал |
|
т.е. |
, тогда |
. |
Записывая эту формулу в координатах, получим, что
2) Комплексная форма ряда Фурье.
Пусть функция f (x) определена в интервале [− π, π]. Применяя формулы Эйлера
можно записать ряд Фурье данной функции в комплексной форме :
Билет №22
1) Оператор Гамильтона (набла). Свойства оператора набла.
Вычисление grad(φ*ψ) и div(grad φ).
. - набла
Свойства:
Если умножить вектор 
на скаляр 
, то получится вектор
,
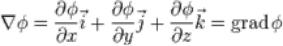который представляет собой градиент функции 
.
Если вектор 
скалярно умножить на вектор 
, получится скаляр
,
то есть дивергенция вектора 
.
Если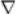 
умножить на 
векторно, то получится ротор вектора 
: