Методы и средства передачи информации (Лекция №8)

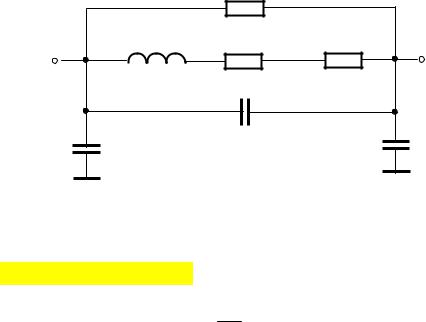
зависимости от частоты. Если пренебречь малой величиной gиз ≈ 0, то полное входное сопротивление в частотной области представляется в виде:

(8.1)

В нашем курсе мы ограничимся описанием резистора идеальной зависимостью u = Ri .

Рисунок 8.1 − Обобщенная эквивалентная схема резистора

Понятие индуктивность отражают эффект электромагнитной индукции

который для идеальной (и линейной) катушки во временнόй области запишется в виде

а в частотной области имеет вид:

U = jω L I, (8.2')

где L – собственная индуктивность катушки.

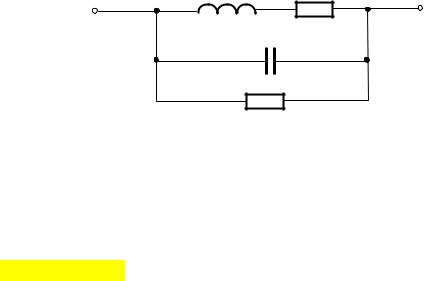
В реальной катушке провод имеет сопротивление, имеются потери в магнитопроводе, а между витками существует распределенная емкость и токи утеч-

ки, характеризуемые проводимостью gиз. С учетом этого в низкочастотном диа-

пазоне катушка индуктивности может быть представлена эквивалентной схемой с сосредоточенными параметрами (рис. 8.2).

2

L R

C

Рисунок 8.2 − Эквивалентная схема катушки индуктивности По структуре и составу элементов эта схема практически не отличается от

эквивалентной схемы резистора (см. рис. 8.1), а, следовательно, имеет качественно аналогичные частотные зависимости.

Конденсатором называют элемент электрической цепи, функциональное назначение которого определяется соотношением между током и напряжением вида:

где q − заряд;

С− коэффициент пропорциональности между напряжением и зарядом, назы-

Идеальный линейный конденсатор − элемент эквивалентной электрической схемы, который характеризуется величиной емкости С=const (u).

В частотной области идеальный линейный конденсатор определяет коэффициент пропорциональности между током и напряжением

Конструктивно оформленный конденсатор обладает рядом паразитных элементов (рис. 8.3), среди которых основными являются последовательные ин-

3

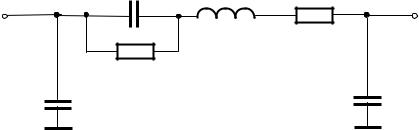
дуктивность L, сопротивление R выводов и обкладок, параллельная проводимость утечки изоляции gиз , емкость обкладок относительно корпуса Cк .

C L R

Рисунок 8.3 − Обобщенная эквивалентная схема «конструктивно оформленного» конденсатора

Полное сопротивление эквивалентной схемы в частотной области при ус-

ловии пренебрежения величинами gиз и Cк имеет вид

где ω0 = (LC) −1/2; ρ = (LC) 1/2; Q = ρ/R.

Из сказанного можно заключить, что применяемые для описания модели длинной линии понятия погонных (т.е. отнесенных к единице длины распределенной структуры) продольного активного сопротивления и поперечной активной проводимости, продольной индуктивности и поперечной емкости − являются некоторыми аналогами известных сосредоточенных элементов, которые в структуре реальных двухпроводных линий и коаксиальных кабелей физически отсутствуют.

Каким же образом в конструктивной реализации конкретной линии передачи (будем относить к ним все виды волноведущих линий (или волноводов), предназначенных для канализации, т.е. передачи, сигналов, начиная от двухпроводных и многопроводных линий, коаксиальных кабелей и заканчивая полыми трубами, т.е. собственно волноводами) возникают параметры погонных сопротивлений, проводимостей, индуктивностей и емкостей? Чтобы ответить на этот вопрос, необходимо проследить процесс формирования понятий напряжение и ток, исходя из более общих понятий − составляющих электромагнитного поля.

4

Так, для описания электростатического поля, исходя из его потенциального характера, вводится понятие скалярный потенциал (в инженерной практике его называют просто − потенциал) φ, связанный с вектором напряженности электрического поля Е формулой Е =−grad φ, которая в прямоугольной (декарто-

l 2

электростатическом поле равна U = ϕ1 − ϕ 2 = ∫Edl , где l − путь перемещения

l1

из точки l1 в точку l2, а dl − касательная к кривой в каждой точке кривой линии l. Понятие «ток» связано с понятием вектора напряженности магнитного поля Н известным соотношением, которое называют «закон полного тока», и кото-

рое в интегральной форме (т.е. для макромоделей) имеет вид: 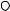∫Hdl = I , где l −

l

замкнутый контур, охватывающий ток I.

Таким образом, в структуре физической двухпроводной линии (рис. 8.4) можно выделить области, в которых проявятся введенные интегральные понятия ток I и разность потенциалов, т.е. напряжение U. Остается открытым вопрос от-

Н

I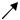

Е

U

−I

Рисунок 8.4 − Схематичное изображение напряжения и тока в двухпроводной линии

носительно связи этих понятий (или характеристик) двухпроводной линии друг с другом и с геометрическими размерами линии и её положением относительно

5

окружающих структур, а также свойств среды размещения, которые в общем случае называют граничными условиями.

Эта связь, в конечном итоге, определится структурой электромагнитного поля (электрической и магнитной составляющих) в линии. Структура поля в линии связана с интегральными параметрами, которые, в свою очередь, определят интересующие на первичные параметры r0 , g 0, L 0 , C 0 линии передачи. Связь

составляющих поля и интегральных параметров линии можно установить на основе решения электродинамической (или, иначе говоря, полевόй) задачи.

Для начала ограничимся качественным рассмотрением структуры полей в частном случае линии передачи − двухпроводной линии.

2. Структура электромагнитных полей двухпроводной линии

Двухпроводная линия − простейшая электродинамическая (полевáя) структура, применяемая для канализации информационных сигналов. Особенность поля в такой структуре проводящих тел заключается в плоскопараллельном характере, т.е. в независимости составляющих поля от продольной координаты линии передачи, что физически объяснимо продольной однородностью и осевой симметрией этой полевой структуры. Это значит, что в поперечной плоскости линии передачи поле описывается системой уравнений на плоскости (т.е. уравнения рассматриваются в двумерной области). Кроме того, в частотном диапазоне, в котором обоснованно применяются такие линии передачи (на практике, это диапазон частот до сотен мегагерц), допустимо приближение независимости электрических и магнитных полей (см. лекция № 2, п. 3). Исходя из этих замечаний, допустимо осуществление независимого анализа электрических и магнитных полей двухпроводной линии в плоскости поперечного сечения.

3. Методы расчета электромагнитных полей

Расчет электростатических полей является важным этапом определения конструктивного параметра – емкости элементов электрических цепей как с сосредоточенными (конденсаторов), так и с распределенными параметрами (удельных или погонных емкостей). В общем случае расчет электростатических полей

6

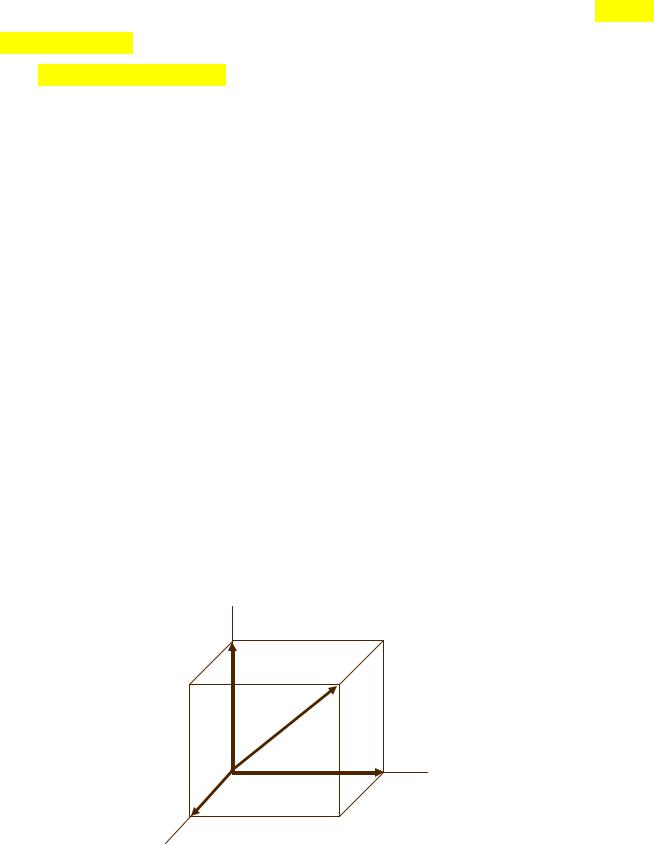
осуществляется интегрированием уравнения Пуассона (или Лапласа) для скалярного потенциала при учете граничных условий.

Скалярный потенциал − вспомогательная функция, характеризующая электростатическое поле, при помощи которой можно выразить состояние поля в любой точке. Физически скалярный электрический потенциал в каждой точке пространства определяется работой, которую нужно затратить на перенос единичного заряда из точки, где потенциал принят равным нулю, в данную точку. Поля, характеризуемые скалярным потенциалом, называются безвихревыми или потенциальными.

В безвихревом поле существует множество точек с одинаковой величиной потенциала, формирующие в общем случае криволинейные поверхности, называемые эквипотенциальными. Любая линия на этих поверхностях называется эквипотенциальной. Например, в случае одиночного точечного заряда (в отсутствии иных зарядов) эквипотенциальными в силу симметрии системы являются сферические поверхности, центрированные в точке расположения заряда.

Наибольшая скорость пространственного изменения потенциала φ в данной точке называется градиентом потенциала и обозначается либо символом grad φ, либо ϕ (см. рис. 8.5). Градиент потенциала – векторная величина нор-

Рисунок 8.5 − Введение понятия градиент скалярной функции

мальная к эквипотенциальной поверхности (или линии на ней) проходящей через данную точку. В разложении на составляющие по координатным направлениям,

7

каждая из которых соответствует скорости изменения функции (потенциала) в данном направлении, в прямоугольной системе координат:

функцию (в частности ϕ). Правило осуществления такого «умножения» опреде-

ляет вид формулы (8.7).

Выражения градиента в цилиндрической и сферической системах учитывают криволинейность координатных осей и приведены в справочниках.

В феноменологической модели электростатического поля градиент потенциала равен пределу отношения силы, с которой поле действует на пробный (точечный, чтобы искажением поля, вносимым присутствием этого заряда можно было пренебречь) отрицательный заряд, к величине этого заряда. Полагается, что при отсутствии инерции у пробного заряда, его движение под действием сил электростатического поля происходило бы по некоторой линии, называемой линией поля или силовой линией, касательная в каждой точке которой есть градиент электрического потенциала поля. Иначе говоря, градиент поля равен напряженности электростатического поля в каждой точке пространства:

Из операций двукратного дифференцирования в теории электромагнитного поля имеет большое применение дивергенция градиента, называемая скалярным лапласианом ( ϕ) или 2 ϕ, обозначаемым ∆ϕ.

Развернутое выражение лапласиана получается с применением правила скалярного произведения векторов . Например, в прямоугольной системе координат с учетом выражения (8.7) получим:

8

Выражения скалярного потенциала в других системах координат приведены в справочниках.

Уравнение Пуассона для скалярного потенциала возникает в результате подстановки в уравнение теоремы Гаусса (см. лекция №2, формула (2.3))

где произведение D понимается в форме скалярного произведения вектора Набла и вектора электрической индукции D) в дифференциальной форме divD =ρ

(или в форме ( ε 0 ε r E) =ρ), выражения связи напряженности поля и потен-

циала: E = − ϕ.

Уравнение Лапласа отличает от уравнения Пуассона равенство нулю правой части (т.е. отсутствие в полевой структуре свободных зарядов).

Однако в ряде практически интересных, но простейших задач, применение уравнения Пуассона не рационально и оказывается более удобным применение непосредственно выражений по закону Кулона или теоремы Гаусса (которая есть математическое представление закона Кулона). Причем при расчете полей в геометрически симметричных моделях теорему Гаусса рационально применить в интегральной форме. Важно понимать, что в инженерной практике большинство реальных полевых структур сводится к достаточно простым моделям, расчет полей в которых можно осуществить указанными выше методами с применение метода суперпозиции.

9

В основе расчета полей с применение интегральных соотношений лежит результат решения задачи о поле точечного заряда q в неограниченном свободном пространстве (рис. 8.6), который с применением теоремы Гаусса для поля центрально симметричной задачи (т.е. при условии Е= r0Еr) имеет вид:

q

ϕ( r ) = 4 πε a r + C . Постоянная интегрирования С определяется из граничных

условий (ГУ), которые можно принять в виде равенства нулю потенциала при r →∞. Откуда С = 0.

α

x

Рисунок 8.6 − Расчет поля точечного заряда в свободном пространстве

10