- •Министерство образования и науки Российской Федерации
- •Введение
- •Постановка задачи и исходные данные
- •Исходные данные
- •1.Оптимизация теплообменного аппарата
- •1.1 Общие сведения о теплообменных аппаратах, их сущность и назначение
- •1.2 Принцип работы кожухотрубчатого теплообменного аппарата
- •1.3 Методика расчета кожухотрубного теплообменного аппарата Тепловой расчет
- •Гидравлический расчет
- •1.4. Метод Ньютона
- •Алгоритм метода Ньютона
- •1.5. Программы оптимизации
- •Текст программы
- •Результаты расчета
- •1.6. Программа оптимизации теплообменного аппарата
- •Текст программы
- •2. Оптимизация выпарной установки
- •2.1. Характеристика процессов выпаривания
- •Аппараты с выносной нагревательной камерой
- •Области применения выпарных аппаратов
- •2.3. Методика расчета однокорпусного выпарного аппарата Исходные данные
- •Тепловой расчет
- •Гидравлический расчет
- •2.4.Программа расчета оптимизации выпарного аппарата Текст программы:
- •Результаты расчета
- •Ректификационные колонны. Компьютерный подход
- •Расчет ректификационных колонн непрерывного действия
- •Математические модели ректификационных колонн
- •Расчет элементов и узлов ректификационных колонн
- •Расчет ректификационных колонн и оптимизация их с помощью эвм
- •Список использованной литературы
Гидравлический расчет
Полное гидравлическое сопротивление при движении жидкости в трубах теплообменного аппарата определяется выражением 1.15:
|
|
(1.15) |
где
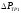 -
гидравлическое сопротивление трения.
-
гидравлическое сопротивление трения.
Гидравлическое сопротивление трения определяется по формуле 1.16:
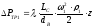 (1.16)
(1.16)
где
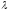 -
коэффициент трения,
-
коэффициент трения,
 -
число ходов теплоносителя по трубному
пространству
-
число ходов теплоносителя по трубному
пространству
Потери давления, обусловленные наличием местных сопротивлений определяются по формуле 1.17:
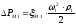 (1.17)
(1.17)
где
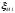 -
сумма коэффициентов местных сопротивлений
трубного пространстваопределяется
по формуле 1.18:
-
сумма коэффициентов местных сопротивлений
трубного пространстваопределяется
по формуле 1.18:
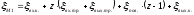 (1.18)
(1.18)
где
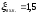 и
и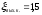 -
коэффициенты сопротивлений входной и
выходной камер.
-
коэффициенты сопротивлений входной и
выходной камер.
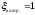 и
и
 - коэффициенты сопротивлений входа в
трубы и выхода из них.
- коэффициенты сопротивлений входа в
трубы и выхода из них.
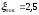 -
коэффициент сопротивления поворота
между ходами.
-
коэффициент сопротивления поворота
между ходами.
Целевая функция (З) представляет собой функцию затрат, включающую в себя капитальные затраты (Зкап) и эксплуатационные затраты (Зэкспл).
Выразив все зависимости через переменные w и dвн, представленные в вышеописанной методике, следующую формулу:
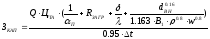

В итоге целевая функция для оптимизации теплообменного аппарата принимает следующий вид 1.19:
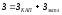 (1.19)
(1.19)
1.4. Метод Ньютона
В основе метода Ньютона лежит квадратичная аппроксимация целевой функции. Последовательность итераций строится таким образом, чтобы во вновь получаемой точке градиент аппроксимирующей функции обращался в нуль.
Последовательность
приближений строится в соответствии
с формулой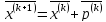 ,
,
где
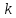 —
номер итерации (
—
номер итерации (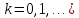 ,
,
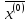 —
начальное
приближение,
—
начальное
приближение,
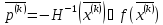 —
вектор
направления спуска.
—
вектор
направления спуска.
Здесь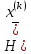 — матрица Гессе.
— матрица Гессе.
Направление
спуска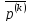 ведет к убыванию целевой функции только
при положительной определенности
матрицы Гессе
ведет к убыванию целевой функции только
при положительной определенности
матрицы Гессе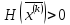 .
В тех итерациях, в которыхматрица Гессе
отрицательно определена
.
В тех итерациях, в которыхматрица Гессе
отрицательно определена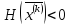 ,последовательность
приближений к точке минимума строится
по методу наискорейшего градиентного
спуска. С этой целью проводится замена
вектора направления спуска на
антиградиентное
,последовательность
приближений к точке минимума строится
по методу наискорейшего градиентного
спуска. С этой целью проводится замена
вектора направления спуска на
антиградиентное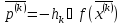 .
.
Алгоритм метода Ньютона
Задать размерность задачи оптимизации п, координаты начальной точки
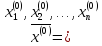 ,
точность поиска
,
точность поиска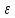 .
.Положить счетчик числа итераций
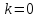 .
.Определить направление вектора градиента целевой
функции
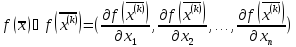
в
точке
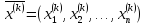 .
Для вычисления координат вектора
градиента использовать разностную
формулу (2.3)
.
Для вычисления координат вектора
градиента использовать разностную
формулу (2.3)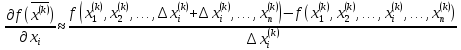 .
.
Проверить условие окончания поиска
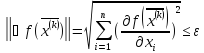
Если
условие выполнено, то расчет окончен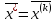 ,
иначе перейти к пункту 5.
,
иначе перейти к пункту 5.
5. Сформировать
матрицу Гессе
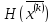 ,
используя разностные формулы
вычисления вторых (2.5) и смешанных
производных (2.6).
,
используя разностные формулы
вычисления вторых (2.5) и смешанных
производных (2.6).
Проверить положительную определенность матрицы
Гессе
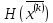 .
Если матрица положительно определена
.
Если матрица положительно определена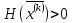 ,
то перейти к пункту 7, иначе — к пункту
8.
,
то перейти к пункту 7, иначе — к пункту
8.
Определить координаты точки
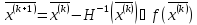 и
перейти к пункту 10.
и
перейти к пункту 10.Вычислить шаг
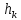 по
формуле (2.4), используя резуль
по
формуле (2.4), используя резуль
таты вычислений пункта 3 и разностные формулы (2.5), (2.6).
Определить координаты точки
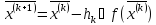 по методу наискорейшего градиентного
спуска.
по методу наискорейшего градиентного
спуска.Положить
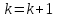 и перейти к пункту 3.
и перейти к пункту 3.
1.5. Программы оптимизации
Для
подтверждения работоспособности
программы минимизации функции, из
учебника [6], решим пример № 2.22. В данном
примере, необходимо найти минимум
целевой функции, методом Ньютона, с
точностью
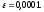
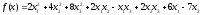
Для разработки программы была использована среда PascalABC.