12

Преобразование системы координат

Пусть имеются две АСК на плоскости и .

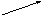
M

Так как - базис, то любой вектор плоскости можно разложить по этому базису

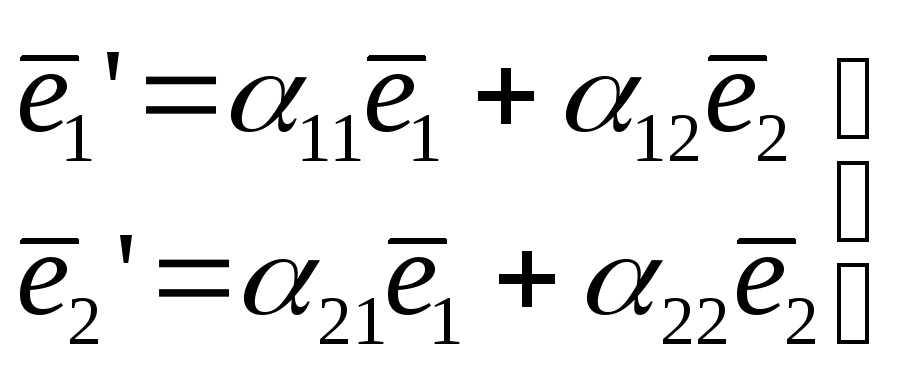
(1)

Необходимо найти связь между и .

(2)

Переход от ПДСК к ПДСК

Пусть даны 2 ПДСК на плоскости и .

Определение:

Система координат на плоскости называется правой, если поворот от первой ко второй оси производится против часовой стрелки; левой, если поворот по часовой стрелке

Определение.

Преобразование системы координат называется собственным, если при этом не меняется ориентация системы координат, и несобственным, если ориентация меняется.

Преобразование ПДСК в ПДСК называется ортогональным преобразованием

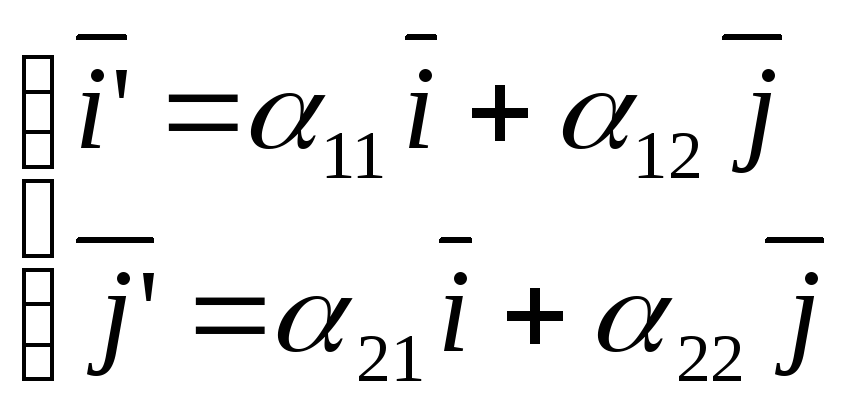(3)

Первый случай: обе системы координат – правые.

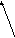
Умножим скалярно на и уравнения системы (3):

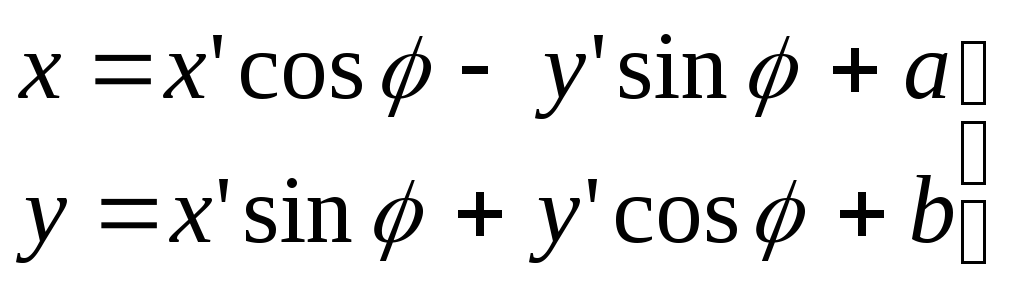(4)

Второй случай: преобразование правой системы координат в левую.

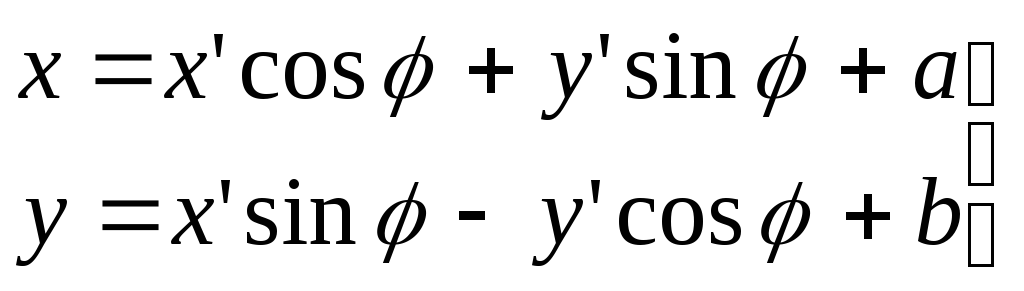(5)

Определитель матрицы перехода для собственного преобразования:

Определитель матрицы перехода для несобственного преобразования:

Полезные соотношения:

Теорема

Если оси ДПСК параллельно переносятся на величину в направлении оси и на величину в направлении оси и, кроме того, поворачиваются на угол при неизменном масштабе, то формулы собственного преобразования координат

Обратное собственное ортогональное преобразование:

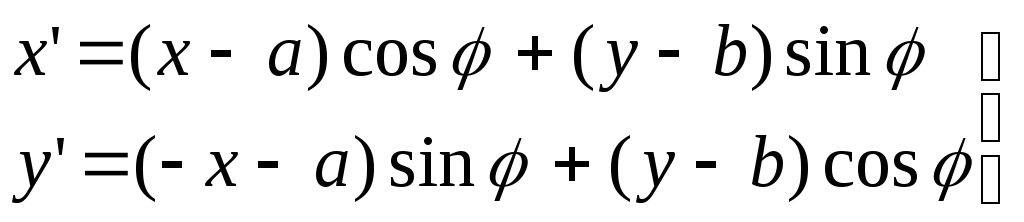(6)

Преобразование ПДСК в пространстве

Углы Эйлера

Преобразование аффинных систем координат

O

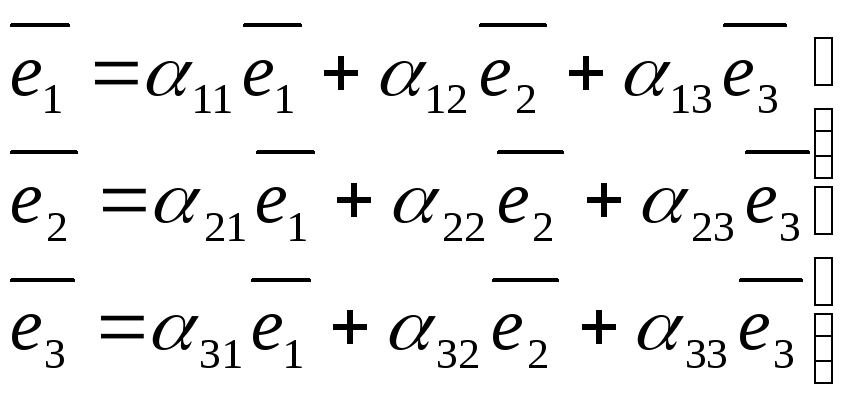(7)

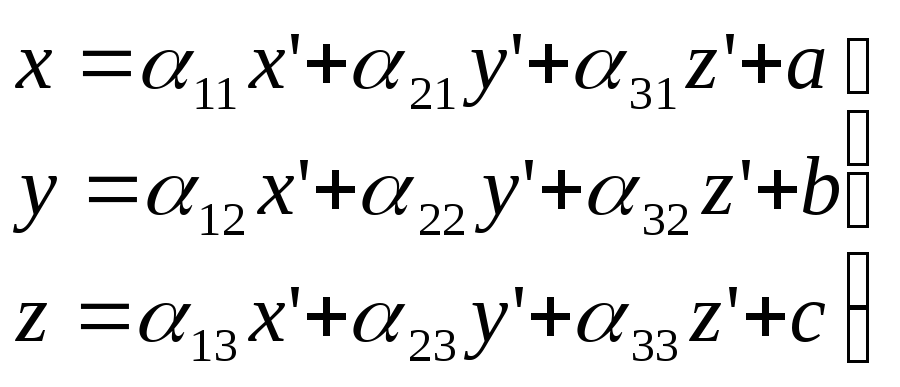(8)

Преобразование ПДСК в пространстве

Даны две ПДСК и (только поворот осей).

Обозначим углы между осями:

.

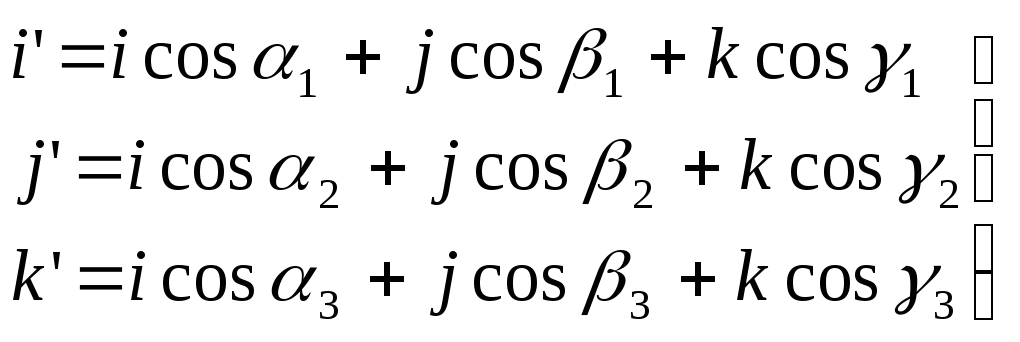(9)

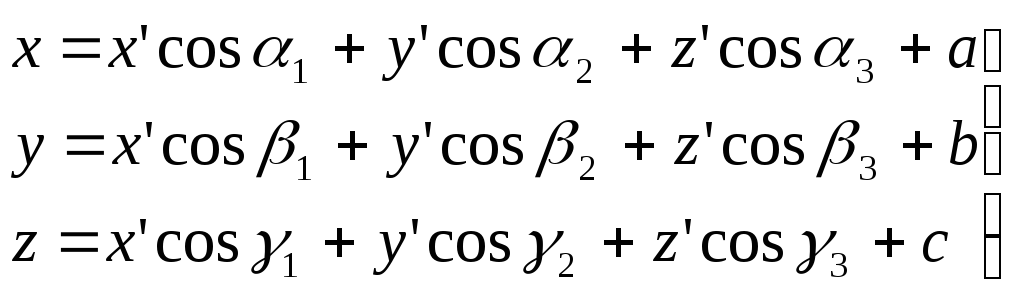(10)

Рассмотрим систему координат.

- пересечение координатных плоскостей xOy и ;

O

– углы Эйлера

Таким образом, переход от ПДСК к ПДСК можно выполнить в три этапа при помощи углов Эйлера.

1) повернём вокруг оси на угол :

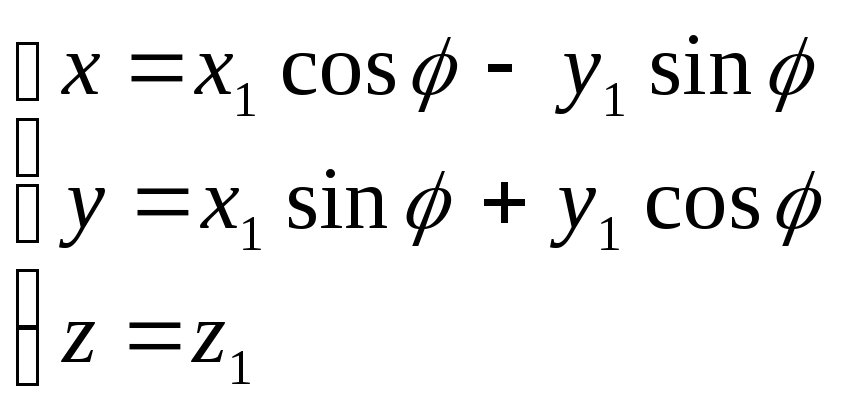
2) повернём вокруг оси () на угол :

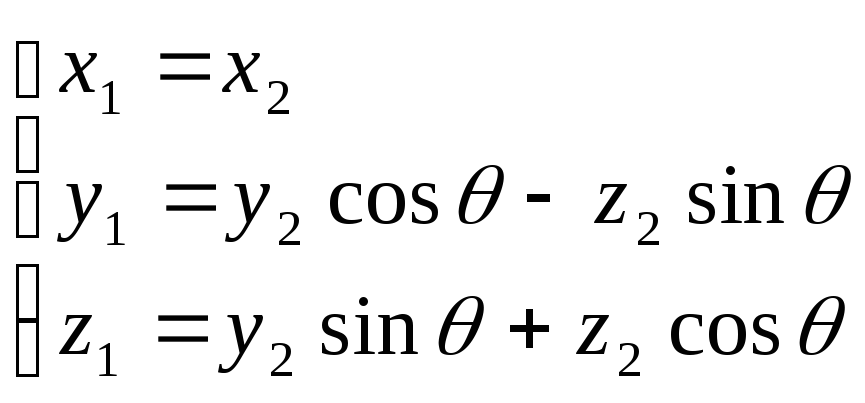
3) повернём вокруг на угол :