АГ Векторная алгебра 2015-16 / 02 Линейная зависимость и независимость системы векторов

6

Линейная зависимость и независимость векторов

Определения линейно зависимой и независимой систем векторов

Определение 22

Пусть имеем систему из n-векторов и имеем набор чисел _, тогда

(11)

называется линейной комбинацией данной системы векторов с данным набором коэффициентов.

Определение 23 (через нулевую линейную комбинацию)

Система векторов называется линейно зависимой, если существует такой набор коэффициентов , из которых хотя бы один не равен нулю, что линейная комбинация данной системы векторов с этим набором коэффициентов равна нулевому вектору:

. (12)

Пусть , тогда

Определение 24 (через представление одного вектора системы в виде линейной комбинации остальных)

Система векторов называется линейно зависимой, если хотя бы один из векторов этой системы можно представить в виде линейной комбинации остальных векторов этой системы.

Утверждение 3

Определения 23 и 24 эквивалентны.

Определение 25 (через нулевую линейную комбинацию)

Система векторов называется линейно независимой, если нулевая линейная комбинация этой системы возможна лишь при всех равных нулю.

Определение 26 (через невозможность представления одного вектора системы в виде линейной комбинации остальных)

Система векторов называется линейно независимой, если не один из векторов этой системы нельзя представить в виде линейной комбинации других векторов этой системы.

Свойства линейно зависимой и независимой систем векторов

Теорема 2 (нулевой вектор в системе векторов)

Если в системе векторов имеется нулевой вектор, то система линейно зависима.

 Пусть , тогда .

Получим , следовательно, по определению линейно зависимой системы векторов через нулевую линейную комбинацию (12) система линейно зависима. 

Теорема 3 (зависимая подсистема в системе векторов)

Если в системе векторов имеется линейно зависимая подсистема, то и вся система линейно зависима.

 Пусть - линейно зависимая подсистема , среди которых хотя бы одно не равно нулю:

Пусть

Значит, по определению 23, система линейно зависима. 

Теорема 4

Любая подсистема линейно независимой системы линейно независима.

 От противного. Пусть система линейно независима и в ней имеется линейно зависимая подсистема. Но тогда по теореме 3 вся система будет также линейно зависимой. Противоречие. Следовательно, подсистема линейно независимой системы не может быть линейно зависимой. 

Геометрический смысл линейной зависимости и независимости системы векторов

Теорема 5

Два вектора и линейно зависимы тогда и только тогда, когда .

 Необходимость.

и - линейно зависимы , что выполняется условие . Тогда , т.е. .

Достаточность.

линейно зависимы. 

Следствие 5.1

Нулевой вектор коллинеарен любому вектору

Следствие 5.2

Для того чтобы два вектора были линейно независимы необходимо и достаточно, чтобы был не коллинеарен _.

Теорема 6

Для того чтобы система из трёх векторов была линейно зависима необходимо и достаточно, чтобы эти векторы были компланарными.

 Необходимость.

- линейно зависимы, следовательно, один вектор можно представить в виде линейной комбинации двух других.

, (13)

где и . По правилу параллелограмма есть диагональ параллелограмма со сторонами , но параллелограмм – плоская фигура компланарны - тоже компланарны.

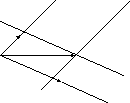
Достаточность.

- компланарны. Приложим три вектора к точке О:

A`

A

C

O

B`

B

– линейно зависимы 

Следствие 6.1

Нулевой вектор компланарен любой паре векторов.

Следствие 6.2

Для того чтобы векторы были линейно независимы необходимо и достаточно, чтобы они были не компланарны.

Следствие 6.3

Любой вектор плоскости можно представить в виде линейной комбинации любых двух неколлинеарных векторов этой же плоскости.

Теорема 7

Любые четыре вектора в пространстве линейно зависимы.

 Рассмотрим 4 случая:

1. Если среди векторов есть нулевой вектор. Тогда система линейно зависима по теореме 2.

2. Если среди векторов имеется хотя бы 1 пара коллинеарных векторов. Тогда система линейно зависима по теоремам 5 и 3.

3. Если среди векторов имеется компланарная тройка векторов. Тогда система линейно зависима по теоремам 6 и 3.

4. Если среди векторов 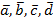нет нулевых векторов, коллинеарных пар и компланарных троек. Приложим эти 4 вектора к точке О.

. Проведем плоскость через векторы , затем плоскость через векторы и плоскость через векторы . Затем проведем плоскости, проходящие через точку D, параллельные парам векторов ; ; соответственно. По линиям пересечения плоскостей строим параллелепипед OB₁D₁C₁ABDC.

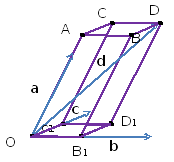
Рассмотрим OB₁D₁C₁ – параллелограмм по построениюпо правилу параллелограмма .

Рассмотрим OADD₁– параллелограмм (из свойства параллелепипеда) , тогда

EMBED Equation.3 .

По теореме 1 такие, что . Тогда , и по определению 24 система векторов линейно зависимая. 

Следствие 7.1

Суммой трёх некомпланарных векторов в пространстве является вектор, совпадающий с диагональю параллелепипеда, построенного на этих трёх векторах, приложенных к общему началу, причём начало вектора суммы совпадает с общим началом этих трёх векторов.

Следствие 7.2

Если в пространстве взять 3 некомпланарных вектора, то любой вектор этого пространства можно разложить в линейную комбинацию данных трёх векторов.