
- •Глава 3. Производная функции одной переменной
- •3.1. Производная функции в точке
- •X Физический смысл производной
- •Геометрический смысл производной. Связь с существованием касательной
- •Уравнения касательной и нормали
- •Бесконечные производные
- •Односторонние производные
- •3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
- •Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
- •Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
- •3.3. Правила вычисления производных
- •3.6. Производные некоторых элементарных функций (таблица производных)
- •3.7. Логарифмическая производная
- •3.8. Производная функции, заданной параметрически
- •3.9. Дифференцирование функций, заданных неявно
- •Глава 4. Производные и дифференциалы высших порядков
- •4.1. Дифференциал функции одной переменной
- •Геометрический смысл дифференциала
- •Инвариантность формы дифференциала первого порядка
- •Дифференциал и приближенные вычисления
- •4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
- •Дифференциалы высших порядков
- •Правила вычисления производной суммы - го порядка. Формула Лейбница для- й производной произведения двух функций
- •4.3. Теоремы о непрерывных и дифференцируемых функциях
- •4.4. Формулы конечных приращений, их приложения
- •Теорема Ролля5о среднем
- •4.5. Раскрытие неопределенностей (Правило Лопиталя)
- •4.6. Формула Тейлора для многочленов
- •4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
- •4.8. Формула Тейлора с остаточным членом в форме Лагранжа
- •Формула Маклорена11
- •4.9. Разложения основных элементарных функций (асимптотические формулы)
- •Глава 5. Исследование и построение графиков функции одной переменной
- •5.1. Условия возрастания и убывания функции
- •5.2. Локальный экстремум Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
- •5.3. Абсолютный экстремум функции
- •5.4. Выпуклость и точки перегиба графика функции
- •Точки перегиба графика функции
- •5.5. Асимптоты графика функции
- •5.6. Схема исследования функций и построения кривых
4.4. Формулы конечных приращений, их приложения
Пусть
функция
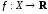 определена на множестве
определена на множестве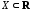 и
и
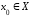 – предельная
точка
– предельная
точка
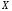 .
.
Теорема Ролля5о среднем
Пусть
функция
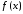 непрерывна на отрезке
непрерывна на отрезке
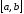 и дифференцируема на
и дифференцируема на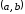 (т.е. во всех внутренних точках). Если
(т.е. во всех внутренних точках). Если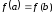 ,
то существует такая точка
,
то существует такая точка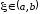 ,
что
,
что
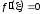 .
.
Доказательство.
Так как
функция
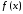 непрерывна
на отрезке
непрерывна
на отрезке
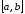 ,
то, по второй теореме Вейерштрасса, в
некоторых точках отрезка она достигает
своих максимального
,
то, по второй теореме Вейерштрасса, в
некоторых точках отрезка она достигает
своих максимального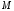 и минимального
и минимального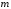 значений на этом отрезке. Если
значений на этом отрезке. Если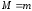 ,
то
,
то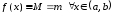 и
и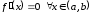 .
.

Пусть
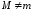 .
Так как
.
Так как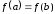 ,
то, по крайней мере, одно из значений
(
,
то, по крайней мере, одно из значений
(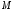 или
или
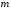 )
достигается во внутренней точке отрезка
)
достигается во внутренней точке отрезка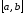 .
Тогда по теореме Ферма в этой точке
производная
.
Тогда по теореме Ферма в этой точке
производная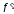 равна нулю. Теорема доказана.
равна нулю. Теорема доказана.
Геометрически
теорема Ролля показывает, что в некоторых
точках интервала
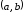 (на рис. 4.4 точки
(на рис. 4.4 точки
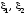 )
касательная к графику функции параллельна
оси
)
касательная к графику функции параллельна
оси .
.
Следствие.
Если функция
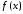 удовлетворяет условиям теоремы Ролля
и
удовлетворяет условиям теоремы Ролля
и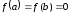 ,
то найдется хотя бы одна точка
,
то найдется хотя бы одна точка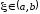 ,
в которой
,
в которой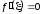 .
Иначе, между двумя нулями функции
найдется хотя бы один нуль производной.
.
Иначе, между двумя нулями функции
найдется хотя бы один нуль производной.
Теорема Лагранжа о среднем
Пусть
функция
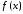 непрерывна на отрезке
непрерывна на отрезке
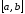 и дифференцируема во всех точках
интервала
и дифференцируема во всех точках
интервала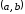 .Тогда
существует точка
.Тогда
существует точка
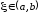 такая, что
такая, что
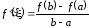 или
или
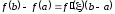 . (4.11)
. (4.11)
Формулу (4.11) называют формулой Лагранжа или формулой конечных приращений.
Доказательство.
Сведем задачу к теореме Ролля. Выберем
число
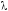 так, чтобы для функции
так, чтобы для функции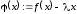 выполнялось
равенство
выполнялось
равенство
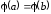 .
Имеем
.
Имеем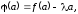
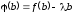 .
Из уравнения
.
Из уравнения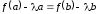 вытекает, что
вытекает, что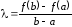 .
Таким образом,
.
Таким образом,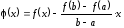 ,
причем
,
причем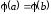 .
Функция
.
Функция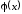 непрерывна на отрезке
непрерывна на отрезке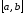 и дифференцируема в интервале
и дифференцируема в интервале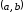 .
По теореме Ролля существует точка
.
По теореме Ролля существует точка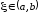 такая, что
такая, что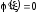 .
Это означает, что
.
Это означает, что
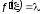 ,
т. е.
,
т. е.
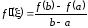 .
.
Теорема доказана.
Следствие
о постоянстве функции, имеющей равную
нулю производную. Пусть
функция
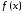 непрерывна на отрезке
непрерывна на отрезке
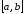 и
и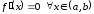 .
Тогда
.
Тогда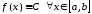 .
.
Рис.
Доказательство.
Пусть
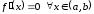 .
Рассмотрим две произвольные точки
.
Рассмотрим две произвольные точки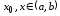 и пусть, например,
и пусть, например,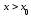 .
Тогда
.
Тогда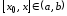 .
По теореме Лагранжа
.
По теореме Лагранжа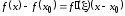 ,
где
,
где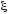 –
некоторая
точка из интервала
–
некоторая
точка из интервала
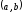 .
Так как
.
Так как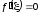 ,
то
,
то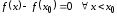 .
Поэтому
.
Поэтому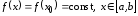 .
.
Геометрический смысл теоремы Лагранжа (рис. 4.5)
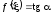 –есть
тангенс угла наклона касательной к
графику функции
–есть
тангенс угла наклона касательной к
графику функции
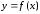 в
точке
в
точке
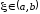 ,
отношение
,
отношение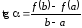 – тангенс угла наклона прямой, соединяющей
точки
– тангенс угла наклона прямой, соединяющей
точки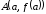 и
и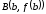 графика функции. Таким образом, теорема
утверждает, что на кривой
графика функции. Таким образом, теорема
утверждает, что на кривой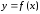 существует точка
существует точка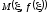 такая, что через эту точку можно провести
касательную параллельно хорде
такая, что через эту точку можно провести
касательную параллельно хорде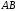 .
.
Теорема Коши6о среднем
Пусть
функции
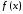 и
и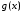 непрерывны
на отрезке
непрерывны
на отрезке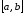 и дифференцируемы в интервале
и дифференцируемы в интервале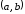 и пусть производная
и пусть производная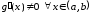 .
Тогда найдется точка
.
Тогда найдется точка
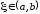 такая, что
такая, что
 . (4.12)
. (4.12)
Доказательство.
Сведем
задачу к теореме Ролля. Введем функцию
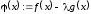 и подберем
число
и подберем
число
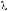 так, чтобы выполнялось равенство
так, чтобы выполнялось равенство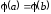 .
Имеем
.
Имеем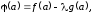
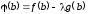 .
Из уравнения
.
Из уравнения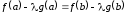 находим
находим
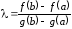 .
(4.13)
.
(4.13)
Заметим,
что
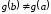 ,
так как в противном случае
,
так как в противном случае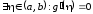 ,
что противоречит условию
,
что противоречит условию
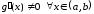 .
Функция
.
Функция
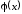 непрерывна на отрезке
непрерывна на отрезке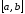 и дифференцируема
и дифференцируема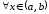 ,
причем
,
причем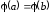 .
По теореме Ролля существует точка
.
По теореме Ролля существует точка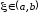 такая, что
такая, что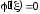 .
Находим
.
Находим
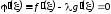 . (4.14)
. (4.14)
Из
(4.14) в силу того, что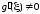 ,
находим
,
находим
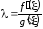 .
С учетом (4.13), получим (4.12). Теорема
доказана.
.
С учетом (4.13), получим (4.12). Теорема
доказана.
Замечание.
Теорема Лагранжа – частный случай
теоремы Коши при
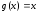 ,
а теорема Ролля – частный случай теоремы
Лагранжа. Во всех этих теоремах речь
идет о существовании некоторого числа
,
а теорема Ролля – частный случай теоремы
Лагранжа. Во всех этих теоремах речь
идет о существовании некоторого числа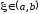 ,
точное значение которого остается
неизвестным. Теоремы Ролля, Лагранжа,
Коши обычно называюттеоремами
о среднем значении.
,
точное значение которого остается
неизвестным. Теоремы Ролля, Лагранжа,
Коши обычно называюттеоремами
о среднем значении.
Сформулированные и доказанные теоремы легли в основу доказательства мощного метода раскрытия неопределенностей, который нашел швейцарский математик Иоганн Бернулли7, но опубликовал французский математик Гийом Лопиталь8.
