
- •Глава 3. Производная функции одной переменной
- •3.1. Производная функции в точке
- •X Физический смысл производной
- •Геометрический смысл производной. Связь с существованием касательной
- •Уравнения касательной и нормали
- •Бесконечные производные
- •Односторонние производные
- •3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
- •Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
- •Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
- •3.3. Правила вычисления производных
- •3.6. Производные некоторых элементарных функций (таблица производных)
- •3.7. Логарифмическая производная
- •3.8. Производная функции, заданной параметрически
- •3.9. Дифференцирование функций, заданных неявно
- •Глава 4. Производные и дифференциалы высших порядков
- •4.1. Дифференциал функции одной переменной
- •Геометрический смысл дифференциала
- •Инвариантность формы дифференциала первого порядка
- •Дифференциал и приближенные вычисления
- •4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
- •Дифференциалы высших порядков
- •Правила вычисления производной суммы - го порядка. Формула Лейбница для- й производной произведения двух функций
- •4.3. Теоремы о непрерывных и дифференцируемых функциях
- •4.4. Формулы конечных приращений, их приложения
- •Теорема Ролля5о среднем
- •4.5. Раскрытие неопределенностей (Правило Лопиталя)
- •4.6. Формула Тейлора для многочленов
- •4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
- •4.8. Формула Тейлора с остаточным членом в форме Лагранжа
- •Формула Маклорена11
- •4.9. Разложения основных элементарных функций (асимптотические формулы)
- •Глава 5. Исследование и построение графиков функции одной переменной
- •5.1. Условия возрастания и убывания функции
- •5.2. Локальный экстремум Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
- •5.3. Абсолютный экстремум функции
- •5.4. Выпуклость и точки перегиба графика функции
- •Точки перегиба графика функции
- •5.5. Асимптоты графика функции
- •5.6. Схема исследования функций и построения кривых
3.6. Производные некоторых элементарных функций (таблица производных)
1.
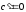 ,
где
,
где – постоянная величина.
– постоянная величина.
2.
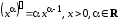 ,
в частности,
,
в частности,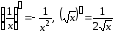 .
.
3.
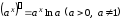 ,
в частности,
,
в частности,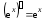 .
.
4.
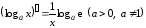 ,
в частности,
,
в частности,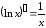 .
.
5.
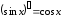 ,
,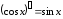 .
.
6.
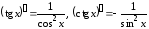 .
.
7.
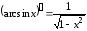 ,
,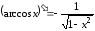 .
.
8.
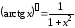 ,
,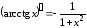 .
.
9.
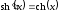 ,
,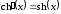 ,
,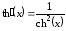 ,
,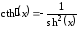 .
.
Докажем справедливость этих формул. Будем использовать определение производной, эквивалентные бесконечно малые и правила вычисления производных.
1.
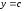 ,
где
,
где – постоянная величина.
– постоянная величина.
Производная
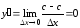 .
.
2.
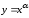 .
.
Производная
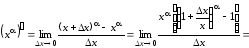
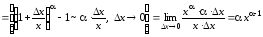 .
.
Для сложной степенной функции имеем формулу производной
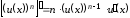
или в краткой записи
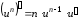 .
.
3.
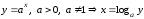 .
.
Пользуясь теоремой о производной обратной функции, находим:
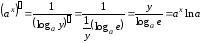 .
.
Для
сложной показательной функции имеем
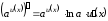 или в краткой записи
или в краткой записи
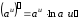 .
.
4.
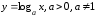 .
.
Приращение
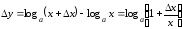 .
.
Производная
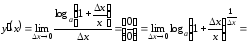
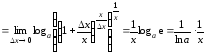 .
.
Для
сложной логарифмической функции
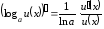 ,
,
или 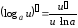 .
.
5.
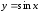 .
.
Ранее было доказано, что
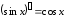 .
.
Для сложной функции
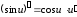 .
.
Для
функции
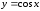 аналогично
аналогично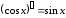 .
.
Для сложной функции
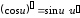 .
.
6.
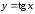 .
.
Производная

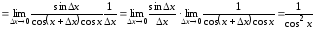
и для сложной функции
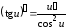 .
.
Производная
функции
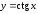 находится аналогично.
находится аналогично.
7.

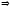
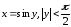 .
.
Пользуясь теоремой о производной обратной функции, находим:
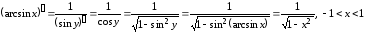 .
.
Для
нахождения производной функции
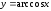 воспользуемся
известной тригонометрической формулой
воспользуемся
известной тригонометрической формулой
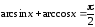 :
:
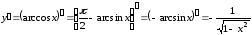 .
.
Для
сложной функции
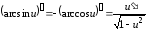 .
.
8.
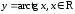
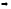
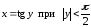 .
.
Производная
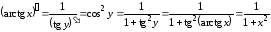 .
.
Для
нахождения производной функции
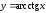 можно воспользоваться
известной тригонометрической формулой
можно воспользоваться
известной тригонометрической формулой
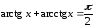 аналогично
предыдущему случаю. Для сложной функции
аналогично
предыдущему случаю. Для сложной функции
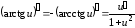 .
.
9. Для нахождения производных этого пункта воспользуемся формулами:
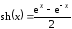 ,
,
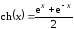 ,
,
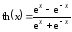 ,
,
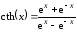
и правилами вычисления производных.
Рассмотрим еще один способ нахождения производных.
3.7. Логарифмическая производная
Определение.
Логарифмической
производной функции
![]() называется производная
называется производная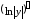 .
.
Так
как
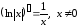 ,
то по правилу дифференцирования сложной
функции получим следующее соотношение
для логарифмической производной
,
то по правилу дифференцирования сложной
функции получим следующее соотношение
для логарифмической производной
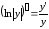 .
(3.6)
.
(3.6)
Если
производную
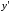 рассматривать как скорость изменения
функцииу,
то величину
рассматривать как скорость изменения
функцииу,
то величину
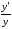 естественно считатьотносительной
скоростью изменения
или темпом
роста функции у.
естественно считатьотносительной
скоростью изменения
или темпом
роста функции у.
С помощью логарифмической производной удобно вычислять производную в тех случаях, когда логарифмирование упрощает вид функции. Такое вычисление основано на формуле
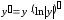 , (3.7)
, (3.7)
полученной из соотношения (3.6) умножением на у.
Используя
формулу (3.7), найдем производную функции
вида
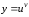 ,
где
,
где ,
,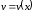 – дифференцируемые функции:
– дифференцируемые функции:
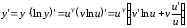 .
.
Пример
3.7. Найти
производную функции
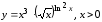 .
.
Найдем
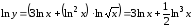 .
.
Дифференцируя
левую и правую часть, получим:
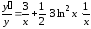 .
Отсюда
.
Отсюда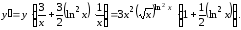
Пример
3.8. Пусть
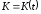 – приближенная
величина вклада в момент времени t.
Можно ли определить (приближенно) ставку
банковского процента
– приближенная
величина вклада в момент времени t.
Можно ли определить (приближенно) ставку
банковского процента
 по функции
по функции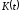 ?
?
Решение.
Пусть
 – номинальная ставка за год,
– номинальная ставка за год,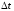 – доля года, тогда проценты за период
времени
– доля года, тогда проценты за период
времени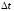 составят
составят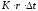 .
Так как приращение вклада и проценты
по вкладу – одно и то же, то
.
Так как приращение вклада и проценты
по вкладу – одно и то же, то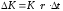 .
Отсюда
.
Отсюда
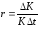 . (3.8)
. (3.8)
Предположим,
что функция
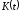 имеет производную
имеет производную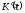 .
Тогда мы можем заменить в равенстве
(3.8) приращение
.
Тогда мы можем заменить в равенстве
(3.8) приращение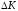 на дифференциал
на дифференциал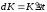 ,
в результате получим
,
в результате получим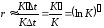 .
.
Вывод:
ставка банковского процента
 совпадает
с логарифмической производной от
величины вклада.
совпадает
с логарифмической производной от
величины вклада.
Упражнение.
Пусть
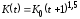 ,
гдеt
– число лет от открытия вклада,
,
гдеt
– число лет от открытия вклада,
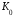 – величина вклада в начальный момент
времениt
= 0. Какой будет ставка банковского
процента: а) через 2 года; б) через 5 лет?
Какова при этом абсолютная скорость
(производная
– величина вклада в начальный момент
времениt
= 0. Какой будет ставка банковского
процента: а) через 2 года; б) через 5 лет?
Какова при этом абсолютная скорость
(производная
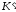 )
роста вклада?
)
роста вклада?
Пример
3.9. Пусть
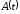 – стоимость некоторого активаА
в момент времени t,
– стоимость некоторого активаА
в момент времени t,
 – доходность от вложения денег в другие
активы. Считаем для простоты, что
– доходность от вложения денег в другие
активы. Считаем для простоты, что не
зависит от
времени. Когда выгодно покупать или
продавать актив А?
не
зависит от
времени. Когда выгодно покупать или
продавать актив А?
Решение.
Найдем
интервал времени, в течение которого
мгновенная доходность актива А
будет больше
 .
Так как мгновенная доходность совпадает
с темпом роста его стоимости, то искомый
интервал времени задается неравенством
.
Так как мгновенная доходность совпадает
с темпом роста его стоимости, то искомый
интервал времени задается неравенством
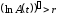 . (3.9)
. (3.9)
Если
неравенство (3.9) задает интервал
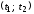 ,
то актив следует купить в момент времени
,
то актив следует купить в момент времени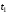 и продать в момент
и продать в момент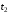 .
Если же множество (3.9) является объединением
двух интервалов
.
Если же множество (3.9) является объединением
двух интервалов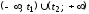 ,
то активА
выгодно продать в момент
,
то активА
выгодно продать в момент
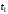 и снова купить в момент
и снова купить в момент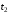 .
.
Упражнение.
Пусть
 =10%
годовых,
=10%
годовых,
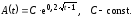 В какой
момент времени выгоднее всего купить
(продать) актив А?
В какой
момент времени выгоднее всего купить
(продать) актив А?
