- •Глава 3. Производная функции одной переменной
- •3.1. Производная функции в точке
- •X Физический смысл производной
- •Геометрический смысл производной. Связь с существованием касательной
- •Уравнения касательной и нормали
- •Бесконечные производные
- •Односторонние производные
- •3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
- •Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
- •Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
- •3.3. Правила вычисления производных
- •3.6. Производные некоторых элементарных функций (таблица производных)
- •3.7. Логарифмическая производная
- •3.8. Производная функции, заданной параметрически
- •3.9. Дифференцирование функций, заданных неявно
- •Глава 4. Производные и дифференциалы высших порядков
- •4.1. Дифференциал функции одной переменной
- •Геометрический смысл дифференциала
- •Инвариантность формы дифференциала первого порядка
- •Дифференциал и приближенные вычисления
- •4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
- •Дифференциалы высших порядков
- •Правила вычисления производной суммы - го порядка. Формула Лейбница для- й производной произведения двух функций
- •4.3. Теоремы о непрерывных и дифференцируемых функциях
- •4.4. Формулы конечных приращений, их приложения
- •Теорема Ролля5о среднем
- •4.5. Раскрытие неопределенностей (Правило Лопиталя)
- •4.6. Формула Тейлора для многочленов
- •4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
- •4.8. Формула Тейлора с остаточным членом в форме Лагранжа
- •Формула Маклорена11
- •4.9. Разложения основных элементарных функций (асимптотические формулы)
- •Глава 5. Исследование и построение графиков функции одной переменной
- •5.1. Условия возрастания и убывания функции
- •5.2. Локальный экстремум Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
- •5.3. Абсолютный экстремум функции
- •5.4. Выпуклость и точки перегиба графика функции
- •Точки перегиба графика функции
- •5.5. Асимптоты графика функции
- •5.6. Схема исследования функций и построения кривых
5.3. Абсолютный экстремум функции
Для
функции
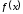 – непрерывной
на отрезке
– непрерывной
на отрезке
 – понятие
– понятие объединяет понятия наибольшего и
наименьшего значений функции на отрезке,
то есть
объединяет понятия наибольшего и
наименьшего значений функции на отрезке,
то есть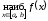 и
и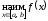 .
.
Наибольшее
(наименьшее) значение непрерывной на
отрезке
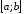 функции
функции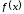 достигается либо в критической точке
этой функции, либо в граничных точкаха и
достигается либо в критической точке
этой функции, либо в граничных точкаха и
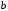 этого отрезка.
этого отрезка.
Для
нахождения
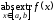 непрерывной на
непрерывной на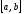 функции
функции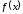 используется
следующая
схема решения.
используется
следующая
схема решения.
1.
Найти
критические точки функции
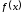 ,
т. е. те значения
,
т. е. те значения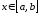 ,
при которых либо
,
при которых либо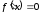 ,
либо
,
либо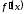 не существует (но в этих точках сама
функция
не существует (но в этих точках сама
функция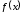 определена и непрерывна).
определена и непрерывна).
2.
Вычислить
значения функции в найденных точках и
на концах
отрезка
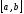 .
.
3.
Найти
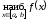 и
и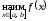 .
Для этого нужно сравнить значения
функции в критических точках (внутри
отрезка) со значениями функции в граничных
точках отрезка и выбрать среди них
наибольшее и, соответственно, наименьшее
значения. (При этом не требуется анализ
характера экстремума этих точек).
.
Для этого нужно сравнить значения
функции в критических точках (внутри
отрезка) со значениями функции в граничных
точках отрезка и выбрать среди них
наибольшее и, соответственно, наименьшее
значения. (При этом не требуется анализ
характера экстремума этих точек).
Часто
вместо
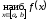 и
и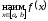 записывают соответственно
записывают соответственно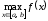 и
и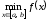 .
.
5.4. Выпуклость и точки перегиба графика функции
Определение.
График
дифференцируемой функции
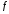 называетсявыпуклым
вверх (выпуклым
вниз) в
интервале (
называетсявыпуклым
вверх (выпуклым
вниз) в
интервале (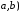 ,
если он расположен не выше (не ниже),
любой своей касательной к графику
функции на этом интервале (рис. 5.3).
,
если он расположен не выше (не ниже),
любой своей касательной к графику
функции на этом интервале (рис. 5.3).
Теорема
5.4
(о
достаточном условии выпуклости вниз
(вверх) графика функции на данном
интервале)

Если
функция
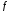 имеет на интервале
имеет на интервале
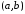 вторую производную и
вторую производную и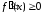
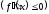 для
для
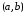 ,
то график функции имеет на
,
то график функции имеет на
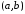 выпуклость, направленную вниз (вверх).
выпуклость, направленную вниз (вверх).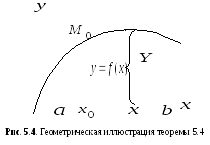
Доказательство.
Допустим,
что
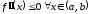 и докажем, что ее график является выпуклым
вверх. Через точку
и докажем, что ее график является выпуклым
вверх. Через точку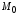 проведем касательную к графику функции
проведем касательную к графику функции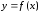 .
Для доказательства теоремы мы должны
установить, что график функции
.
Для доказательства теоремы мы должны
установить, что график функции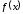 на
на
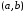 расположен не выше своей касательной
на этом интервале. Пусть
расположен не выше своей касательной
на этом интервале. Пусть – произвольная точка из
– произвольная точка из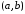 ,
,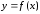 – ордината графика функции в точке
– ордината графика функции в точке .
Далее
.
Далее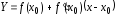 – ордината касательной, соответствующая
значению
– ордината касательной, соответствующая
значению .
Найдем
.
Найдем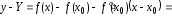
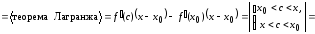
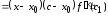 ,
,
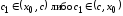 .
Имеем
.
Имеем
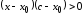 , (5.1)
, (5.1)
так
каклибо
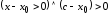 ,
либо
,
либо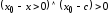 .
По условию теоремы
.
По условию теоремы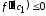 .
Поэтому, с учетом (5.1),
.
Поэтому, с учетом (5.1),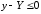 ,
,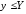 ,
т. е. график функции
,
т. е. график функции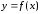 направлен выпуклостью вверх на
направлен выпуклостью вверх на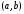 .
.
Аналогично
доказывается, что при
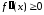 график
функции является выпуклым вниз. Теорема
доказана.
график
функции является выпуклым вниз. Теорема
доказана.
Точки перегиба графика функции
Определение.
Точка
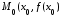 называетсяточкой
перегиба графика функции
называетсяточкой
перегиба графика функции
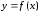 ,
если существует такая окрестность точки
,
если существует такая окрестность точки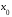 ,
в пределах которой, слева и справа от
нее, направления выпуклости графика
функции различны (рис. 5.5).
,
в пределах которой, слева и справа от
нее, направления выпуклости графика
функции различны (рис. 5.5).
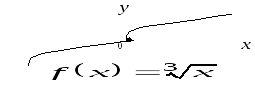
Пример
5.4. Для
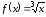 график функции (рис. 5.6) выпуклый вниз
на
график функции (рис. 5.6) выпуклый вниз
на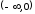 и выпуклый вверх на
и выпуклый вверх на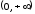 .
Точка перегиба графика функции
.
Точка перегиба графика функции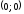 .
.
Пример
5.5. Для
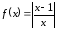 график функции
(см. рисунок
5.7) выпуклый вниз на
график функции
(см. рисунок
5.7) выпуклый вниз на
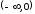 и на
и на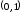 ,
выпуклый вверх на
,
выпуклый вверх на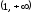 .
Точка перегиба графика функции
.
Точка перегиба графика функции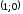 .
Заметим, что
здесь точка
.
Заметим, что
здесь точка
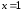 является точкой локального минимума
функции.
является точкой локального минимума
функции.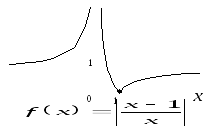
Теорема 5.5 (о необходимом условии существования точки перегиба)
Если
функция
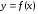 имеет перегиб в точке
имеет перегиб в точке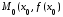 ,
то
,
то
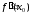 =0,
или
=0,
или
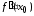 не существует.
не существует.
Доказательство.
Пусть
точка
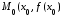 разделяет промежутки выпуклости вниз
и вверх (рис. 5.5). Пусть при
разделяет промежутки выпуклости вниз
и вверх (рис. 5.5). Пусть при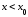 кривая
кривая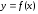 выпукла вниз, а при
выпукла вниз, а при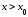 кривая
кривая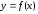 выпукла вверх. Тогда при
выпукла вверх. Тогда при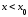 вторая производная
вторая производная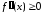 и, значит,
и, значит,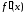 возрастает. При
возрастает. При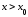
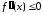 и, значит,
и, значит,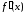 убывает. Это означает, что функция
убывает. Это означает, что функция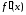 имеет максимум в точке
имеет максимум в точке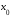 ,
следовательно, ее производная
,
следовательно, ее производная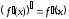 в этой точке или равна нулю, или не
существует.
в этой точке или равна нулю, или не
существует.
Замечание.
Необходимое условие точки перегиба не
является достаточным. Например, функция
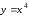 является выпуклой вниз, так как
является выпуклой вниз, так как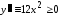 и, значит, не имеет точек перегиба, хотя
и, значит, не имеет точек перегиба, хотя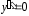 при
при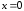 .
.
Определение.
Точки,
в которых
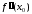 =0
или
=0
или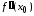 не существует, называюткритическими
точками второго рода.
не существует, называюткритическими
точками второго рода.
Чтобы выяснить, является ли критическая точка точкой перегиба, требуется проверить достаточные условия.
Теорема 5.6 (о достаточных условиях существования точки перегиба)
Пусть
функция
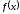 определена
в окрестности
точки
определена
в окрестности
точки
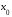 ,
в которой либо
,
в которой либо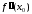 =0,
либо
=0,
либо
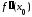 не существует и пусть
не существует и пусть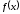 дважды
непрерывно дифференцируема в проколотой
окрестности этой точки. Точка
дважды
непрерывно дифференцируема в проколотой
окрестности этой точки. Точка
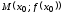 является точкой перегиба графика
функции, если
является точкой перегиба графика
функции, если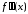 меняет знак при переходе через точку
меняет знак при переходе через точку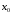 .
.
Доказательство.
Пусть,
например,
вторая
производная
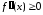 при
при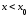 и
и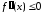 при
при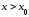 .
В этом случае (рис. 5.5) слева от
.
В этом случае (рис. 5.5) слева от
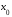 график
функции выпуклый вниз, а справа от
график
функции выпуклый вниз, а справа от
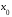 выпуклый вверх, т. е.
выпуклый вверх, т. е.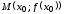 – точка
перегиба графика функции.
– точка
перегиба графика функции.
Пример
5.6. Исследовать
на выпуклость, найти точки перегиба
графика функции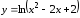 (рис.5.9).
(рис.5.9).
Область
определения
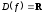 .
При
.
При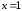 значение функции
значение функции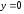 .
Производная
.
Производная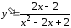 .
Точка
.
Точка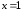 является точкой минимума функции:
является точкой минимума функции: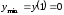 .
Вторая производная равна
.
Вторая производная равна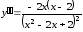 .
Знаки второй производной:
.
Знаки второй производной: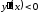 при
при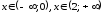 ,
,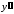
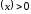 при
при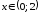 .
При
.
При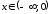 и
и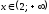 график функции выпуклый вверх; на
интервале
график функции выпуклый вверх; на
интервале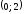 – выпуклый вниз. График меняет направление
выпуклости в двух точках:
– выпуклый вниз. График меняет направление
выпуклости в двух точках: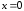 и
и
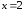 (рис. 5.8). Поэтому точки перегиба графика
функции
(рис. 5.8). Поэтому точки перегиба графика
функции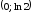 и
и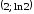 .
.
График
данной функции представлен на рис. 5.9.