
- •Основные понятия и определения
- •Предмет изучения
- •Структура курса
- •Этапы проектирования
- •Основные требования к машинам
- •1.Правильный учет величины и характера нагрузок и условий работы.
- •2. Создание предохранительных устройств
- •3. Правильный выбор материалов и применение поверхностного упрочнения деталей.
- •4. Максимальное использование принципа стандартизации.
- •Нарезание конических колес методом обкатки
- •Влияние z на форму и прочность зуба
- •Критерии работоспособности деталей
- •Формулы для расчета тел на прочность
- •Расчет по предельным состояниям.
- •Расчеты на усталостную прочность
- •Влияние срока службы детали на допускаемое напряжение при постоянном нагружении переменной нагрузкой
- •Термостойкость делится на теплостойкость и хладостойкость.
- •Машиностроительные материалы и термическая обработка
- •Термическая обработка:
- •Механические передачи
- •Ориентировочные значения основных параметров передач вращательного движения
- •Зубчатые передачи
- •Расчет зубьев на изгибную прочность
- •Расчет зубьев на прочностьпри воздействии максимальной (пиковой) нагрузки
- •Особенности геометри косозубых и шевронных зубчатых колес
- •Коэффициент перекрытия косозубых передач. Расчеты на прочность цилиндрических косозубых и шевронных передач
- •Усилия в зубчатых цилиндрических передачах
- •Допускаемые напряжения
- •Окружной и нормальный модули в косозубой передаче
- •Расчеты на прочность цилиндрических косозубых и шевронных передач. Эквивалентное прямозубое колесо
- •Шевронные передачи конические зубчатые передачи.
- •Формы зуба конического колеса
- •Нарезание прямозубых и тангенциальных конических колес Зависимости углов начальных конусов δ1 и δ2 от передаточного числа
- •Радиусы дополнительных конусов
- •Силы в конических прямозубых передачах
- •Силы натяжения ремня в передаче трением
- •Вывод формулы Эйлера
- •Найдем силы f1 и f2 в ведущей и ведомой ветвях ремня.
- •Напряжения в ремне
- •Нагрузки на валы и опоры
- •Расчет ремней (общие положения)
- •Для примера рассмотрим ремень с хлопчатобумажным кордом.
- •Клиноременная передача
- •Выбор клиновых ремней
- •Расчет клиновых ремней
- •Достоинства:
- •Критерии работоспособности и расчета
- •Цепные передачи
- •Зубчатые цепи
- •Звездочки
- •Геометрические и кинематические параметры цепных передач
- •Кинематика цепной передачи
- •Фрикционные передачи
- •Трение в кинематических парах
- •Виды разрушения подшипников
- •Критерии расчета подшипников
- •Расчет на долговечность
- •Расчет подшипников по статической грузоподъемности
- •Особенности расчета радиально-упорных подшипников
- •Способы фиксации валов в корпусе
- •Фиксация подшипников на валу
- •Подшипники скольжения.
- •Конструкция подшипника скольжения
- •Сварные соединения
- •Электродуговая
- •Газовая сварка
- •2. Электродуговая сварка под флюсом.
- •3. Электрошлаковая сварка, также как две предыдущие – сварка плавлением при прохождении тока через шлаковую ванну от электрода к изделию.
- •Контактная сварка.
- •Стыковые швы,
- •Контактная сварка
- •Паяные и клеевые соединения Паяные
Особенности геометри косозубых и шевронных зубчатых колес
Прямозубые колеса обладают существенным недостатком, который заключается в том, что их работа при больших скоростях сопровождается ударами. Причинами их возникновения являются погрешности при изготовлении зубьев и деформации. Удары вредно отражаются не только на прочности колес, но и других узлов машин и вызывают специфический шум.
При больших скоростях наиболее эффективным средством, обеспечивающим плавность и бесшумность работы, является применение колес с косыми и шевронными зубьями.
У
косозубых колес зубья располагаются
не по образующей делительного цилиндра,
а составляют с ней некоторый угол
![]() .
В отличие от прямозубых колес, в которых
зубья входят в зацепление одновременно
по всей длине, в косозубых зубья входят
в зацепление постепенно, благодаря чему
они работают более плавно и бесшумно.
.
В отличие от прямозубых колес, в которых
зубья входят в зацепление одновременно
по всей длине, в косозубых зубья входят
в зацепление постепенно, благодаря чему
они работают более плавно и бесшумно.
Для нарезания косозубых колес используется инструмент такого же исходного профиля, как и для нарезания прямых, поэтому профиль косого зуба в его нормальном сечении совпадает с профилем прямого зуба. Модуль в нормальном сечении является стандартным.
Однако
косозубые колеса имеют и существенный
недостаток. В результате винтового
расположения зубьев возникает осевая
составляющая нормального усилия, которая
обозначается
![]() и называется осевым усилием
и называется осевым усилием
![]() ,
,
г
 де
де![]() ─ угол наклона зуба к оси вращения на
образующей делительного цилиндра.
Величина этой осевой составляющей, так
же как плавность и нагрузочная способность,
зависит от угла наклона зуба
─ угол наклона зуба к оси вращения на
образующей делительного цилиндра.
Величина этой осевой составляющей, так
же как плавность и нагрузочная способность,
зависит от угла наклона зуба![]() .
С увеличением угла
.
С увеличением угла![]() повышается плавность и бесшумность
работы передачи, увеличивается нагрузочная
способность, но увеличивается и осевое
усилие
повышается плавность и бесшумность
работы передачи, увеличивается нагрузочная
способность, но увеличивается и осевое
усилие![]() .
При больших значениях
.
При больших значениях![]() в конструкциях передач приходится
предусматривать специальные опоры,
которые воспринимают эти силы, конструкция
при этом усложняется.
в конструкциях передач приходится
предусматривать специальные опоры,
которые воспринимают эти силы, конструкция
при этом усложняется.
В связи
с этим угол наклона
![]() в косозубых передачах принято выполнять
в пределах от 8 до 160.
При таких значениях обеспечиваются, с
одной стороны, достаточно высокая
плавность и нагрузочная способность
передачи, с другой стороны, небольшое
значение величины осевой составляющей
в косозубых передачах принято выполнять
в пределах от 8 до 160.
При таких значениях обеспечиваются, с
одной стороны, достаточно высокая
плавность и нагрузочная способность
передачи, с другой стороны, небольшое
значение величины осевой составляющей
![]() не требует установки опор сложной
конструкции.
не требует установки опор сложной
конструкции.
В
косозубых колесах различают окружной
шаг
![]() ,
измеренный в торцевом сечении колеса,
и нормальный шаг
,
измеренный в торцевом сечении колеса,
и нормальный шаг![]() ,
измеренный в плоскости, нормальной к
рабочей поверхности зуба
,
измеренный в плоскости, нормальной к
рабочей поверхности зуба![]() (рис.1.13).
(рис.1.13).
В
соответствии с этим в косозубых колесах
имеются два модуля: модуль окружной
![]() и модуль нормальный
и модуль нормальный![]() .
Нормальный модуль является расчетным
и стандартным. Модуль окружной имеет
дробное значение
.
Нормальный модуль является расчетным
и стандартным. Модуль окружной имеет
дробное значение![]() .
.
Диаметр делительной окружности косозубого колеса
![]() .
(1.40)
.
(1.40)
Межосевое расстояние цилиндрической косозубой передачи, образованной колесами без коррекции
![]() . (1.
41)
. (1.
41)
Коэффициент перекрытия косозубых передач. Расчеты на прочность цилиндрических косозубых и шевронных передач
Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в этом сечении принято определять через параметры эквивалентного прямозубого колеса. Профиль зуба эквивалентного колеса соответствует профилю зуба косозубого колеса в его нормальном сечении.
Рассечем
косозубое колесо нормальной к рабочей
поверхности зуба плоскостью n
─ n
(рис. 1.14).
В сечении получим эллипс с полуосями а
и с.
Проведем окружность радиусом
![]() ,
равным радиусу кривизны эллипса в точкеk.
Эту окружность примем за делительную
эквивалентного прямозубого колеса, к
расчету которого сводится расчет
рассматриваемого косозубого. Все
величины, относящиеся к эквивалентному
колесу, условимся обозначать с индексом
,
равным радиусу кривизны эллипса в точкеk.
Эту окружность примем за делительную
эквивалентного прямозубого колеса, к
расчету которого сводится расчет
рассматриваемого косозубого. Все
величины, относящиеся к эквивалентному
колесу, условимся обозначать с индексом
![]() .
Установим связь между величинами,
относящимися к прямозубому и косозубому
колесам.
.
Установим связь между величинами,
относящимися к прямозубому и косозубому
колесам.

Радиус
кривизны эллипса в точке k
: ![]() .
.
Полуоси
эллипса: ![]() ;
;![]() ;
;
откуда
![]() и
и![]() .
.
Ширина
bwV
и диаметр dV
делительной окружности зубчатого венца
эквивалентного колеса соответственно
равны ![]() .
.
Поскольку
![]() ,
то
,
то![]() ,
откуда приведенное число зубьев
эквивалентного колеса равно
,
откуда приведенное число зубьев
эквивалентного колеса равно![]() .
.
Минимальное число зубьев цилиндрической косозубой передачи
![]() ,
,
Откуда
![]() .
.
Или
![]()
Крутящий
момент на эквивалентном колесе
равен ![]() .
.
С учетом
того что
![]() ,
,
где Т─ расчетный крутящий момент на косозубом колесе, получим
![]() .
.
Подставим
значения
![]() ,
,![]() ,
,![]() ,
,![]() в ранее полученные формулы для проектного
и проверочного расчетов прямозубых
цилиндрических колес.
в ранее полученные формулы для проектного
и проверочного расчетов прямозубых
цилиндрических колес.
При
этом примем среднее значение коэффициента
перекрытия
![]() ;
угла наклона зуба
;
угла наклона зуба![]() и коэффициент формы зуба будем определять
с учетом приведенного числа зубьев
и коэффициент формы зуба будем определять
с учетом приведенного числа зубьев![]() .
После преобразования получим формулы,
которые используют при расчете стальных
косозубых колес с углом
.
После преобразования получим формулы,
которые используют при расчете стальных
косозубых колес с углом![]()
 ; (1.42)
; (1.42)
 ; (1.43)
; (1.43)
![]() ; (1.44)
; (1.44)
![]() ; (1.45)
; (1.45)
![]() . (1.46)
. (1.46)
З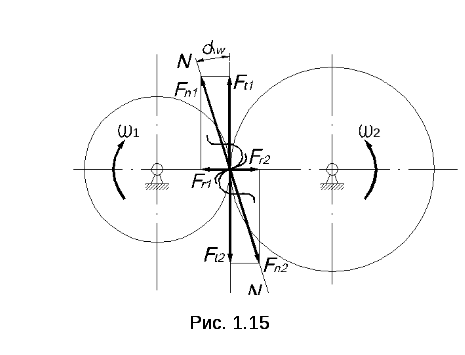 десь
десь![]() ─
коэффициент, учитывающий наклон зубьев,Yε─
коэффициент, учитывающий перекрытие
зубьев:
─
коэффициент, учитывающий наклон зубьев,Yε─
коэффициент, учитывающий перекрытие
зубьев:
Yε = 1/εα .
Здесь εα ─ коэффициент перекрытия передачи
