
- •Вопрос 7. Сила давления жидкости на плоские поверхности. Определение координат центра давления.
- •Вопрос 8. Сила давления жидкости на цилиндрическую поверхность. Центр давления силы. Тело давления.
- •Вопрос 9. Закон Архимеда. Теория плавания тел. Понятие остойчивости плавающих тел.
- •Вопрос 10. Виды движения жидкости. Параметры потока.
- •Параметры потока.
- •Вопрос 11. Дифференциальные уравнения движения жидкости. Уравнение неразрывности несжимаемой жидкости.
- •Вопрос 12. Уравнение Бернулли для струйки невязкой жидкости. Два аспекта членов уравнения Бернулли. Графическое представление уравнения Бернулли для невязкой жидкости. Уравнение Бернулли для газов.
Параметры потока.
Живое сечение потока – поверхность, проведенная нормально к линиям тока.
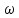 –площадь
живого сечения.
–площадь
живого сечения.
Смоченный периметр - χ – часть длины периметра живого сечения, соприкасающегося с жесткими стенками потока.
 –гидравлический
радиус –отношение площади живого
сечения потока к смоченному периметру.
–гидравлический
радиус –отношение площади живого
сечения потока к смоченному периметру.
Расход потока – количество жидкости, протекающей в единицу времени через живые сечения потока:
 ,
u
– местная (фактическая) скорость.
,
u
– местная (фактическая) скорость.
 –средняя
скорость – одинаковая для всех точек
живого сечения потока скорость, при
которой расход будет таким же, как при
фактических местных скоростях.
–средняя
скорость – одинаковая для всех точек
живого сечения потока скорость, при
которой расход будет таким же, как при
фактических местных скоростях.
Виды движений:
Равномерным
наз такое установившееся движение
потока, при котором S
сечений и
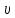 в них будут неизменными по всей его
длине. Если хотя бы один из параметровS
или
в них будут неизменными по всей его
длине. Если хотя бы один из параметровS
или
 изменяется, то движение –неравномерное.
изменяется, то движение –неравномерное.
Плавноизменяющиеся движение - движение хар-ся следующими свойствами:
1) Кривизна линии тока в потоке незначительна.
2) Угол расхождения м/д отдельными линиями тока весьма мал.
3) Живые сечения потока являются плоскими, нормальными к оси потока.
4) Давление по живому сечению распределяется по гидростатическому закону (линейному).
Вопрос 11. Дифференциальные уравнения движения жидкости. Уравнение неразрывности несжимаемой жидкости.
 ,
,
 ,
,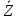 – координаты,
– координаты,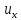 ,
,
 ,
, – скорости,P,
– скорости,P,
 – давление и плотность.- 8 величин,
характеризующих движение каждой частицы
жидкого тела.
– давление и плотность.- 8 величин,
характеризующих движение каждой частицы
жидкого тела.
Задача гидродинамики – установить этих величин от координат времени t и пространства x, y, z.
Выведем основные дифференциальные уравнения, устанавливающие эту взаимосвязь. Выделим в движущейся жидкости элементарно малый объем в форме параллелепипеда.
Сумма проекций всех
сил на ось х (уравнение равновесия на
основании принципа Даламбера), включая
силу инерции
 , отнесенная к единице
массы жидкости, т е после сокращения на
, отнесенная к единице
массы жидкости, т е после сокращения на
 ,
дает нам уравнение
,
дает нам уравнение
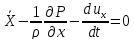 ,
составим аналогичные уравнения
относительно осей y,
z.
,
составим аналогичные уравнения
относительно осей y,
z.
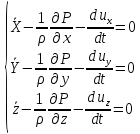 дифференциальные уравнения движения
не вязкой жидкости (ур Эйлера)
дифференциальные уравнения движения
не вязкой жидкости (ур Эйлера)
Так как
 – функция четырех переменных, то её
полный диф-л:
– функция четырех переменных, то её
полный диф-л:
 , разделим на dt
:
, разделим на dt
:
 ,
аналогично
,
аналогично
 и
и
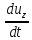 .
.
Знаем, что производные от координаты движущейся точки по времени представляет собой соответствующие проекции её скорости, а подставляя их в уравнение и перенеся члены, содержащие скорости, в правую часть, получаем уравнения:
 общие диф. уравнения
движения жидкости
общие диф. уравнения
движения жидкости
Уравнение неразрывности несжимаемой жидкости (картинка та же)
Неразрывным потоком капельной жидкости называется поток, в котором внутри жидкости отсутствуют как пустоты, так и переуплотнения.
Пусть жидкость
входит в параллелепипед по оси х и её
скорость равна
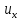 ,
на противоположной грани, на расстоянии
,
на противоположной грани, на расстоянии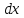 ,
скорость будет
,
скорость будет
 .
.
Тогда количество
входящей жидкости:
 ,
а выходящей:
,
а выходящей: .
.
Масса входящей
жидкости:
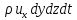 ,
а выходящей:
,
а выходящей: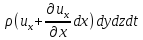 .
.
Изменение массы жидкости в объеме параллелепипеда от движения параллельно оси х:
 ,
аналогично
,
аналогично
 ,
,
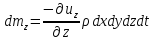
Сложим полученные
изменения массы жидкости:
 ,
т к из-за условия сплошности изменение
массы не должно произойти!
,
т к из-за условия сплошности изменение
массы не должно произойти!
Разделим это уравнение
на
 ,
получимуравнение
неразрывности потока в виде:
,
получимуравнение
неразрывности потока в виде:

 ,
,
 (Расход
потока),
(Расход
потока),
тогда т к потерь нет
(не происходит накопление жижкости в
одном из сечениий лил сжатия - в другом),
то
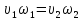 ,
тогда
,
тогда
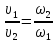 –уравнение
неразрывности в гидравлическом виде
–уравнение
неразрывности в гидравлическом виде
