
7_Основные теоремы строительной механики
.doc
Основные теоремы строительной механики.
Определение перемещений
-
Общие понятия
Δ – перемещения от внешних воздействий;
δ – перемещения от единичных безразмерных сил
ΔiF = δiF∙F
ΔiF = ∑δiF∙Fn
-
Работа сил. Потенциальная энергия деформации
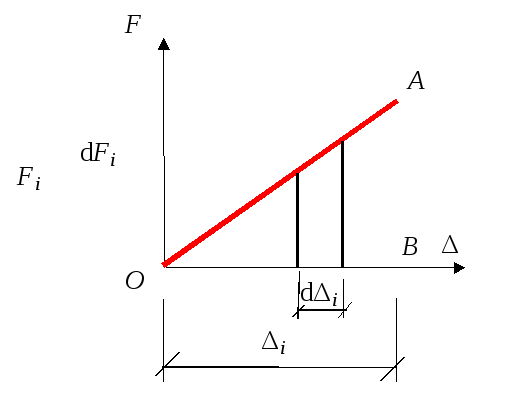
dT = dFi∙dΔi


(теорема Б. Клайперона)





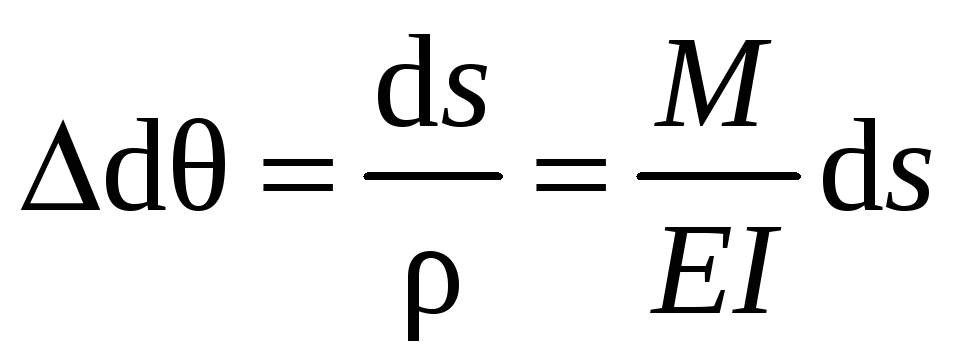




 .
.

Mi, Qi и Ni – силы, совершающие работу
Mk, Qk и Nk – силы, вызывающие деформации


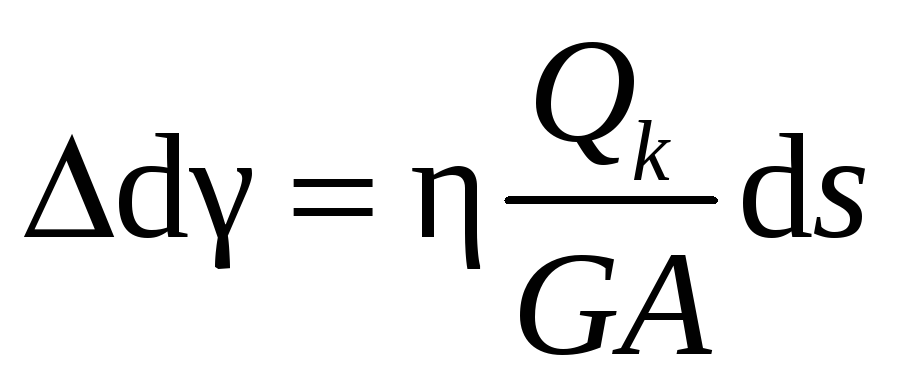



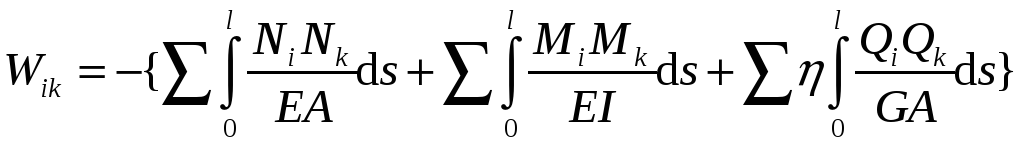

T = – W
-
Принцип возможных перемещений
(принцип Ж. Лагранжа)
Для того, чтобы система, имеющая идеальные связи, находилась в равновесии, необходимо и достаточно, чтобы сумма элементарных работ всех приложенных к ней сил на любой совокупности возможных перемещений равнялась нулю.

– Rq∙ΔК + RB ∙ΔB – F1∙ΔС + F2∙ΔF = 0
Rq = 1,2q
ΔС = Δ ΔB = Δ/1,2
ΔК = 0,5Δ ΔF = 0,25Δ
–1,2ql∙0,5Δ + RB∙Δ /1,2– 0,5ql∙Δ + +ql∙0,25Δ = 0
RB = 1,02 ql
Если упругая деформируемая система под действием приложенных к ней внешних сил находится в равновесии, то при всяком возможном бесконечно малом перемещении точек этой системы сумма работ её внешних и внутренних сил равна нулю.
-
Основные теоремы строительной
механики
Теорема о взаимности возможных рабоn
(теорема Бетти)

Ti= 0,5 Fi Δii + Fi Δik + 0,5 Fk Δkk
Tk = 0,5 Fk Δkk + Fk Δki + 0,5 Fi Δii
Ti = Tk
Fi Δik = Fk Δki
Tik = Tki
Возможная работа сил состояния i на перемещениях, вызванных силами состояния k, равна возможной работе сил состояния k на перемещениях, вызванных силами состояния i.
Теорема о взаимности возможных
перемещений
(теорема Максвелла)
Δki = δkiFi
Δik = δikFk
FiΔik = Fk Δki
FiδikFk = FkδkiFi
δik = δki
Возможное перемещение по направлению i от единичной безразмерной силы, приложенной по направлению k, численно рано возможному перемещению по направлению k от единичной безразмерной силы, приложенной по направлению i.
Теорема о взаимности возможных реакций
(теорема Рэлея)

Rii∙0 – Rki∙Δk = – Rik∙Δi + Rkk∙0
Rki∙Δk = Rik∙Δi
Rki = rki∙Δi Rik = rik∙Δk
rki∙Δi∙Δk = rik∙Δk ∙Δi
rik = rki
Возможная реакция в связи i от единичного смещения связи k численно равна возможной реакции в связи k от смещения связи i.
-
Определение перемещений от внешней нагрузки

ТFk = 1∙ΔkF


− при определении перемещений в фермах

− при определении перемещений в изгибаемых системах


− при определении перемещений в комбинированных системах

Вспомогательные состояния при определении перемещений



Способы “перемножения” эпюр
− способ Верещагина

Mk = x tg α

MF dx = dΩ
x∙MF dx = xdΩ
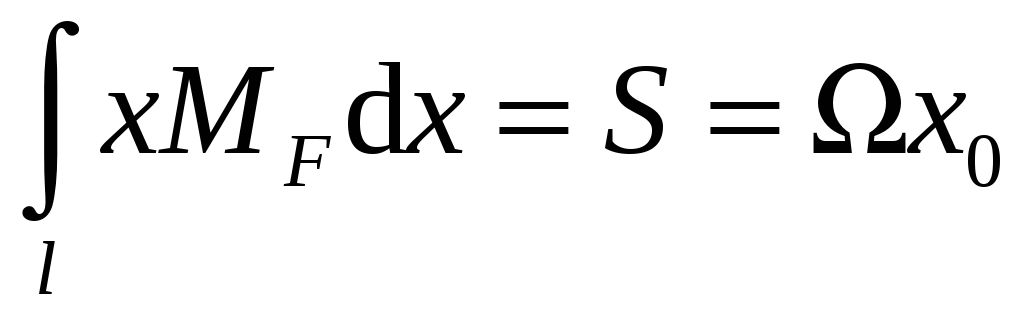


Площади и центры тяжести простейших геометрических фигур


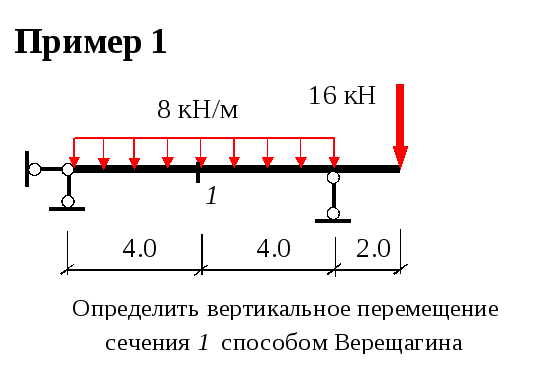



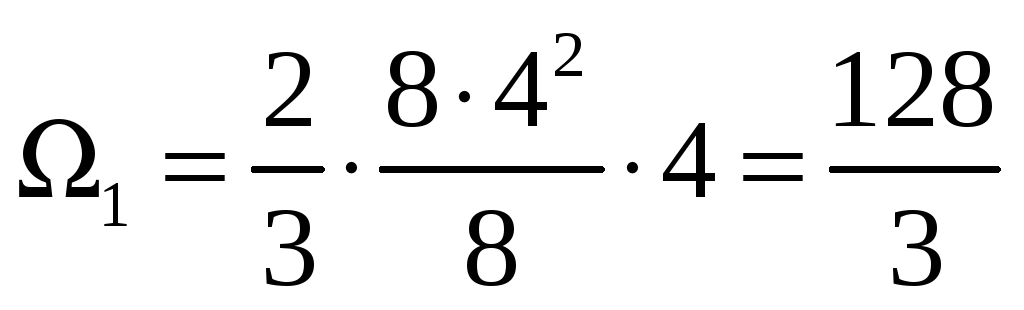
, y01= 1;
Ω2 = 0,5∙48∙4 = 96, y02 = 2∙2/3 = 4/3;
Ω3 = Ω2 = 96, y03 = y02 = 4/3;
Ω4 = Ω1 = 128/3, y04 = y01 = 1;
Ω5 = 0,5∙32∙4 = 64, y02 = 1∙2/3 = 2/3.

− использование формул “перемножения” эпюр
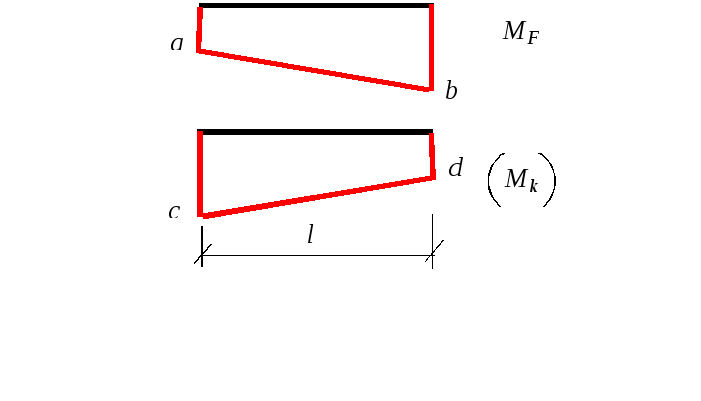



h1 = 0,5∙2 = 1,
h2 = 0,5∙2 = 1,
f1 = 0,5∙48 + 8·42/8 = 40,
f2 = 0,5∙(48 –32) + 8·42/8 = 24.

Пример 2

Пояса :
∟80 х 50 х 6 (A1 = = 2∙7,55 = 15,1 см2)
EA1 = 2,06∙108∙15,1∙10-4 = 31,106∙104 кН = EA
Решётка:
∟50 х 5 (A2 = 2∙4,8 = 9,6 см2)
EA2 = 2,06∙108∙9,6∙10-4 = 19,776∙104 кН = 0,636EA
Определить изменение угла между левой стойкой и раскосом во второй панели






Пример 3





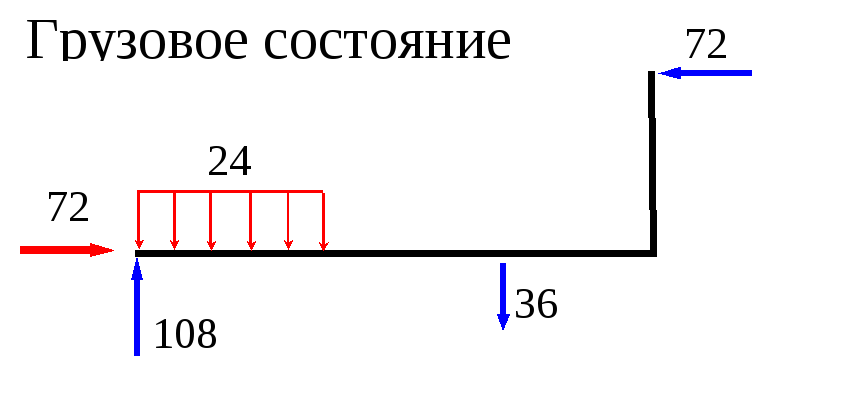


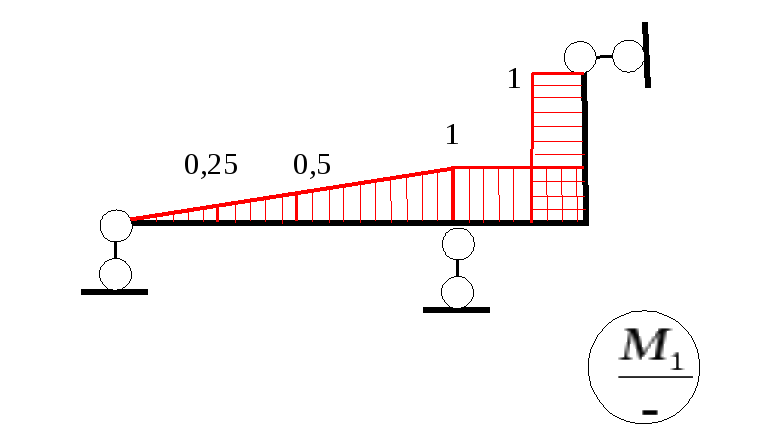







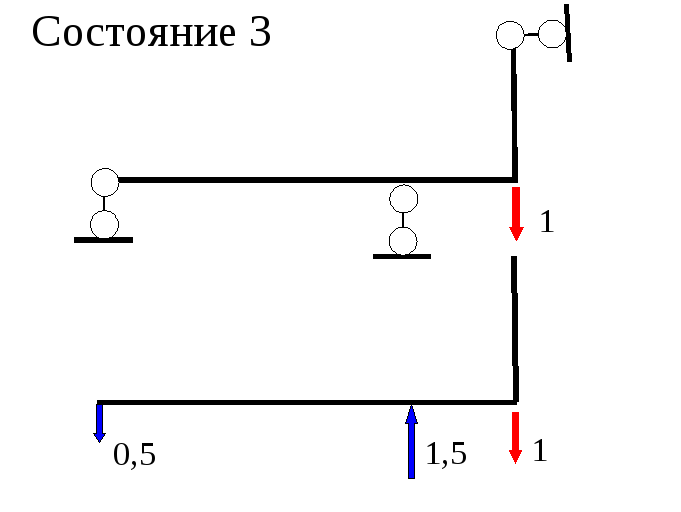
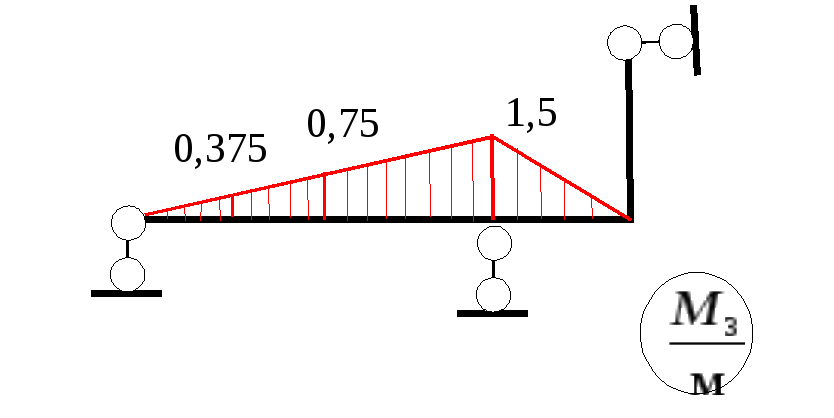






-
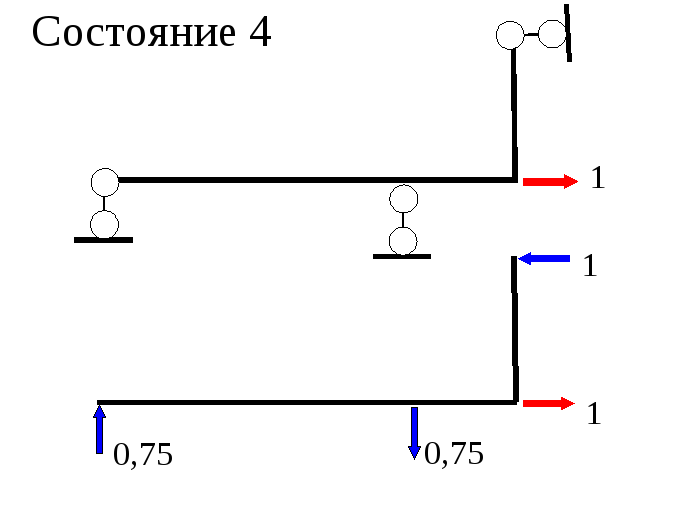
Определение перемещений от теплового воздействия


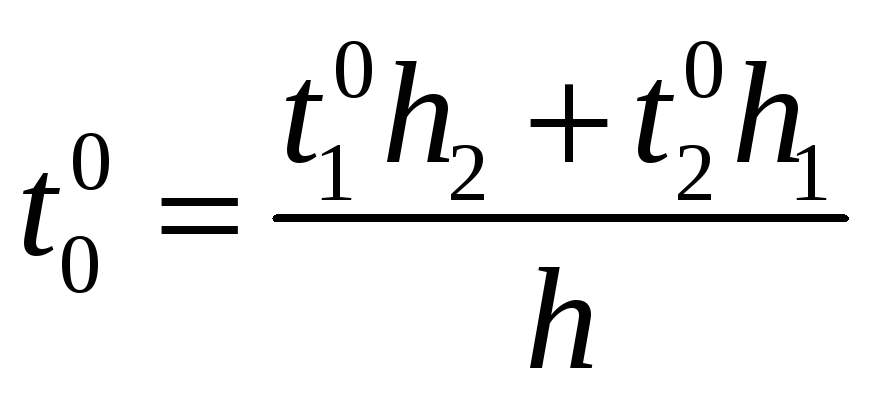









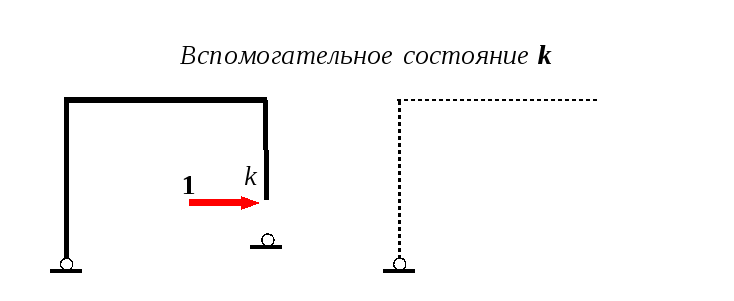
Ttk = 1∙ Δkt

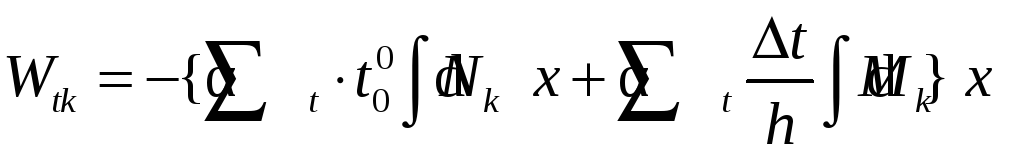



Ttk = – Wtk
Формула для определения перемещений от теплового воздействия
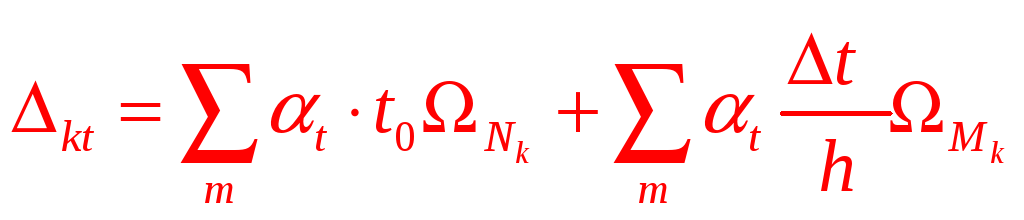 .
.
Пример 5

Левая стойка:
t01 = 0,5(– 45º + 15º) = –15ºС;
Δt1 = |15º – (– 45º)| = 60ºС
Правая стойка:
t02 = 0,5(45º + 150) = 30ºС;
Δt2 = |15º – 45º | = 30ºС



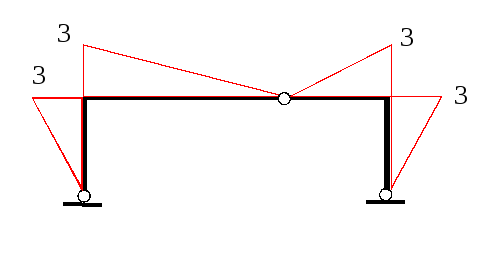

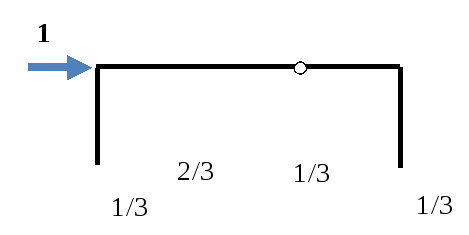
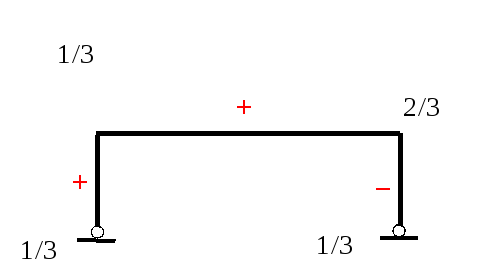



Удлинения стержней:
левая стойкая
Δl1t =αtt01l1= 120∙10-7∙(– 15º)∙4,5 =
= – 0,081∙10-2 м;
правая стойка
Δl2t =αtt02l2= 120∙10-7∙30º ∙4,5 = 0,162∙10-2 м

-
Определение перемещений
от неравномерной осадки опор и
неточности изготовления стержней

TΔk = 1∙ΔkΔ + R1∙Δ1 + R2∙Δ2 +…+ +Ri∙Δi +…+ Rn∙Δn =
=1∙ΔkΔ +∑ Rik∙Δi
WΔk = 0
TΔk = WΔk = 0
Формула для определения перемещений от неравномерной осадки опор
ΔkΔ = – ∑Rik∙ Δi
Формула для определения перемещений от неточности изготовления стержней
ΔkΔ = ∑Nik∙Δi
Пример 6
 Определить
угол поворота сечения К
и построить деформированную схему балки
Определить
угол поворота сечения К
и построить деформированную схему балки

φK = Δ1Δ = – (0,05∙0,06 – 0,125∙0,08 – – 0,375∙0,04 + 0,25∙0,02) = – 0,01 рад.

Пример 5

Определить смещение опоры В, если затяжка изготовлена короче на 0,06 м; построить деформированную схему рамы

ΔВ = Δ1Δ = 2∙(– 0,06) = – 0,12 м
