1.9. Признак сходимости Даламбера Теорема. Пусть для ряда с положительными членамисуществует предел отношения последующего члена ряда к предыдущему, равный:

.

Тогда: 1) ряд сходится, если ;

2) Ряд расходится, если .

Доказательство. 1. Пусть сначала . Выберем число, для которого. Тогда существует номертакой, что при всех натуральныхвыполняется неравенство

.

Отсюда последовательно получаем:

;

; (*)

; … и т.д.

Рассмотрим теперь остаток исходного ряда:

(11)

Поскольку ряд

,

образованный геометрической прогрессией со знаменателем , где, сходится (п. 1.3), то в силу неравенств (*) сходится и остаток (11), а значит, и сам ряд.

2. Если , то существует номертакой, что при всех натуральныхвыполняется неравенство

,

и общий член ряда не может стремиться к нулю. Следовательно, по необходимому признаку содимости ряд расходится. ■

Замечание. При «признак не работает»: существуют примеры как сходящихся, так и расходящихся рядов с (см. ниже п. 1.10).

Пример. По определению факториала:

при .

Рассмотрим при фиксированном ряд. Здесь. Имеем

.

Следовательно ряд сходится. По необходимому признаку сходимости отсюда следует, что

. (12)

Равенство (12) будет использовано в дальнейшем.

1.10. Интегральный признак сходимости Коши

Теорема. Пусть для ряда с положительными членами 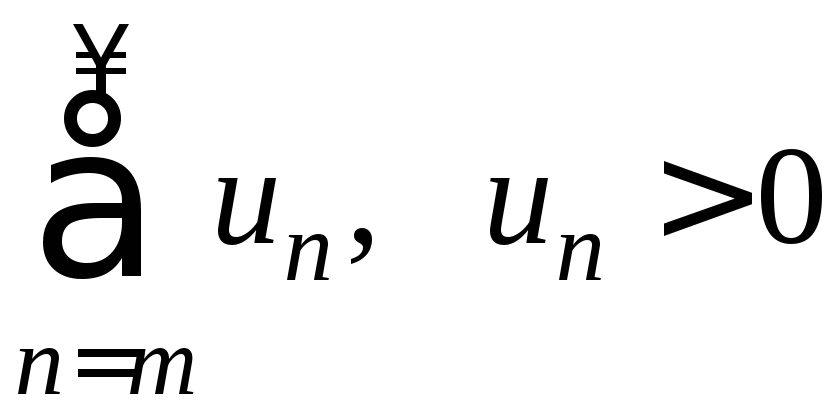, существует функция, удовлетворяющая трем условиям:

1) при некотором натуральном функциянепрерывна на;

2) монотонно убывает на;

3) члены ряда являются значениями этой функции при це-

лых значениях аргумента: .

Тогда ряд сходится или расходится одновременно с несобственным интегралом .

Доказательство. Для удобства обозначений проведем доказательство приПусть— частичная сумма ряда,—натуральное число. Поскольку функцияубывает, то при всехвыполняется неравенство:

.

Проинтегрируем его по отрезку длиной:

.

Суммируя почленно неравенства при и применяя свойство аддитивности определенного интеграла, получаем:

.

Итак,

. (*)

Если несобственный интеграл сходится и равен :,

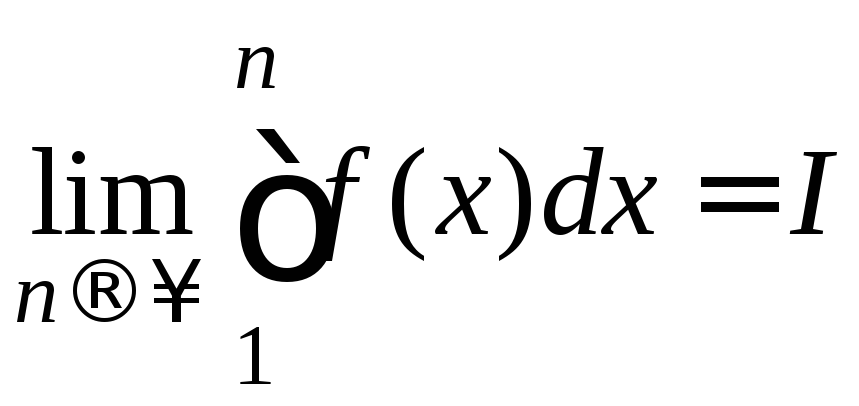так что при всех выполняется неравенство

,

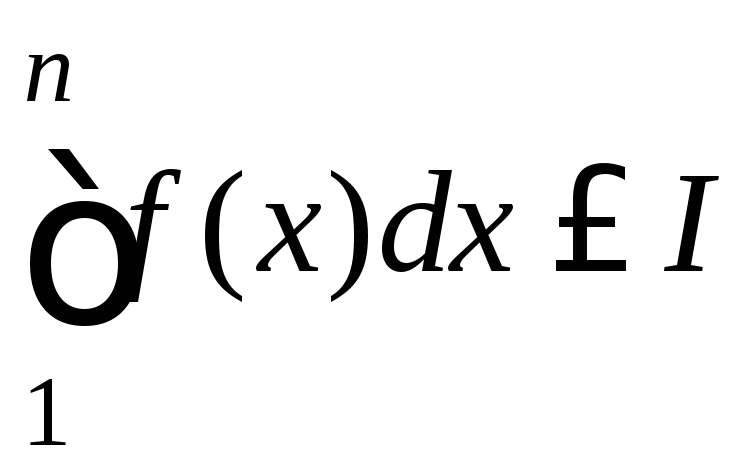то по левому неравенству в (*) возрастающая последовательность ограничена сверху:

;

следовательно, она имеет конечный предел, и ряд сходится.

Если же несобственный интеграл расходится:

,

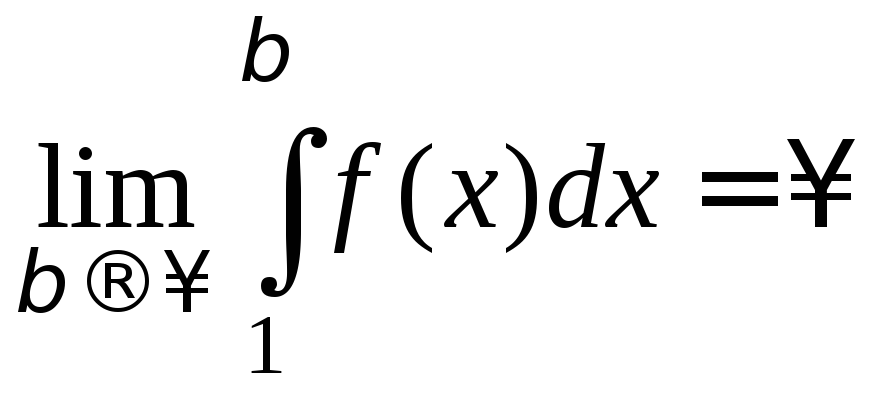то последовательность неограниченно возрастает. Тогда в силу правого неравенства в (*) имеем:; ряд расходится. ■

Примеры. 1.Гармоническим рядом называется ряд

.

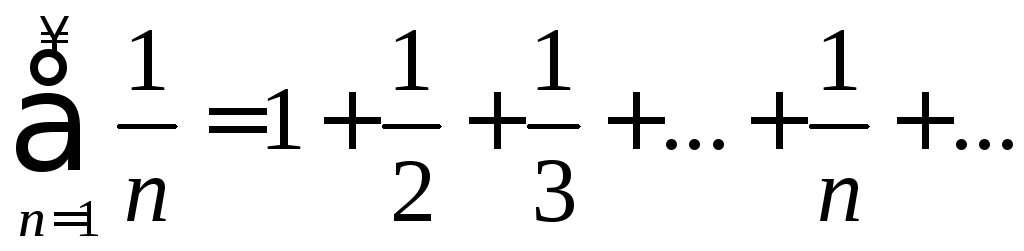Убедимся, что гармонический рядрасходится.С учетом вида общего члена ряда положими применим интегральный признак Коши. Исследуем сходимость несобственного интеграла:

.

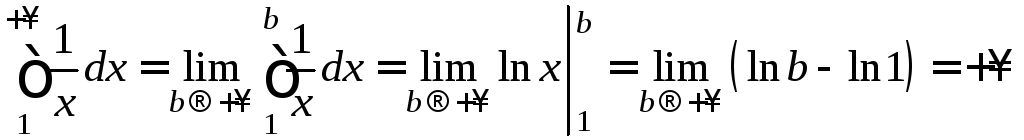Несобственный интеграл расходится, следовательно, гармонический ряд расходится.

2.Обобщенным гармоническим рядомназывается ряд. Исследуем сходимость обобщенного гармонического ряда при. (Приряд заведомо расходится, поскольку общий член ряда в этом случае не стремится к нулю).

При получается обычный гармонический ряд, который расходится. Пусть теперь. Снова применим интегральный признак Коши с функциейи исследуем сходимость несобственного интеграла:

.

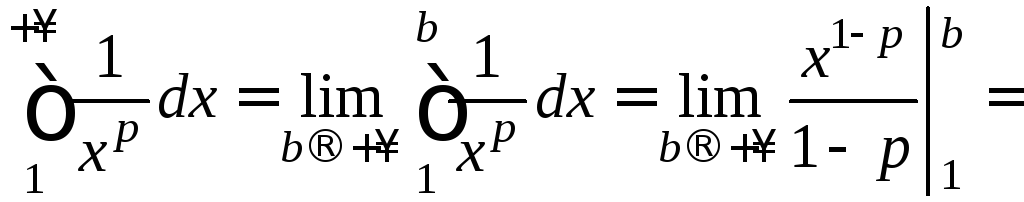
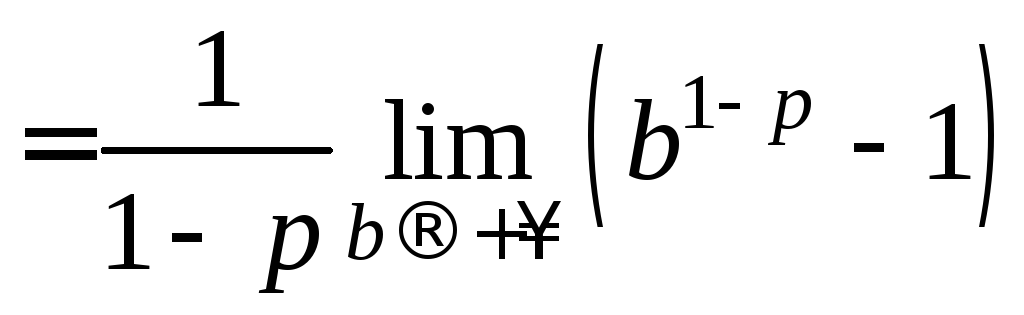Рассмотрим два случая:

1. Если , то показатель степени, и. Несобственный интеграл расходится, следовательно, ряд также расходится.

2. Если , то показатель степени, и. Несобственный интеграл сходится, следовательно ряд также сходится.

Итак, обобщенный гармонический ряд сходится при и расходится при.

Заметим, что признак Даламбера в случае обобщенного гармонического ряда приводит к :

.