
- •Федеральное агентство морского и речного
- •1.1. Сходимость числового ряда
- •Частичные суммы образуют числовую последовательность; эта последовательность может иметь конечный или бесконечный предел, либо не иметь предела.
- •1.3. Ряд, образованный геометрической прогрессией
- •1.4. Остаток ряда
- •1.5. Арифметические свойства сходящихся рядов
- •1.6. Ассоциативность сходящихся рядов
- •1.7. Признаки сравнения положительных рядов
- •1.8. Радикальный признак сходимости Коши
- •1.9. Признак сходимости Даламбера Теорема. Пусть для ряда с положительными членамисуществует предел отношения последующего члена ряда к предыдущему, равный:
- •2) Ряд расходится, если .
- •1.10. Интегральный признак сходимости Коши
- •Тогда ряд сходится или расходится одновременно с несобственным интегралом .
- •1.11. Знакочередующиеся ряды
- •1.12. Абсолютная и условная сходимость
1.7. Признаки сравнения положительных рядов
Будем рассматривать ряды с положительными членами
![]() (8)
(8)
и
![]() ,
(9)
,
(9)
где
![]() при всех
при всех![]() .
.
Частичные
суммы этих рядов
![]() и
и![]() ,
соответственно, будучи составлены из
положительных слагаемых, монотонно
возрастают с ростом числа слагаемых
,
соответственно, будучи составлены из
положительных слагаемых, монотонно
возрастают с ростом числа слагаемых![]() .
.![]()
Теорема
(признак сравнения по неравенству).
Пусть
при всех
![]() выполняется неравенство:
выполняется неравенство:![]() .
Тогда:
.
Тогда:
1) если ряд (9) с бóльшими членами сходится, то ряд (8) с меньшими членами также сходится;
2) если ряд (8) с меньшими членами расходится, то ряд (9) с бóльшими членами также расходится.
Доказательство.
1. Пусть сначала ряд (9) сходится и имеет
сумму
![]() ;
при этом (в силу строгой монотонности
последовательности
;
при этом (в силу строгой монотонности
последовательности![]() )
при всех
)
при всех![]() :
:![]() .
.
Ввиду
неравенства
![]() ,
аналогичное неравенство выполняется
и для частичных сумм:
,
аналогичное неравенство выполняется
и для частичных сумм:![]() ,
так что
,
так что
![]() .
(10)
.
(10)
Итак,
последовательность
![]() частичных сумм ряда (8) монотонно
возрастает и ограничена сверху числом
частичных сумм ряда (8) монотонно
возрастает и ограничена сверху числом![]() .
Тогда по теореме Вейерштрасса существует
предел последовательности
.
Тогда по теореме Вейерштрасса существует
предел последовательности![]() и ряд (8) сходится.
и ряд (8) сходится.
2.
Пусть теперь ряд (8) расходится. Тогда
последовательность частичных сумм
![]() неограниченно возрастает, и в силу
неравенства
неограниченно возрастает, и в силу
неравенства![]() последовательность
последовательность![]() также неограниченно возрастает;
следовательно, ряд (9) расходится. ■
также неограниченно возрастает;
следовательно, ряд (9) расходится. ■
Примеры.
1.
Рассмотрим ряд
![]() .
Сравним его с рядом
.
Сравним его с рядом![]() ,
который сходится, поскольку образован
геометрической прогрессией со знаменателем
,
который сходится, поскольку образован
геометрической прогрессией со знаменателем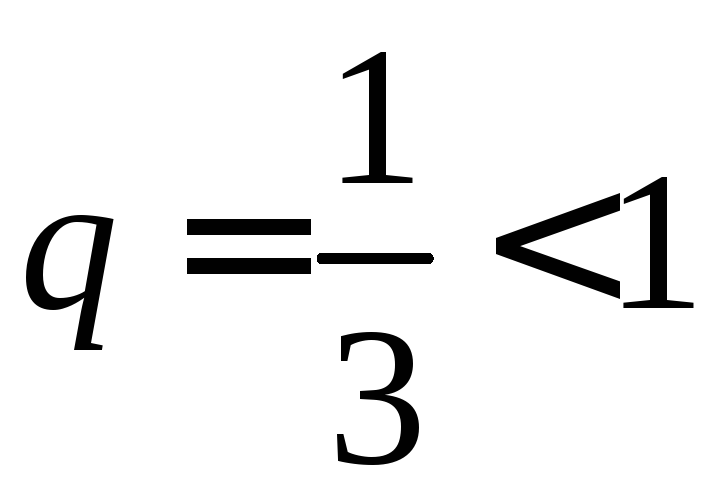 .
Ввиду неравенства
.
Ввиду неравенства![]() ,
исходный ряд также сходится.
,
исходный ряд также сходится.
2.
Рассмотрим ряд
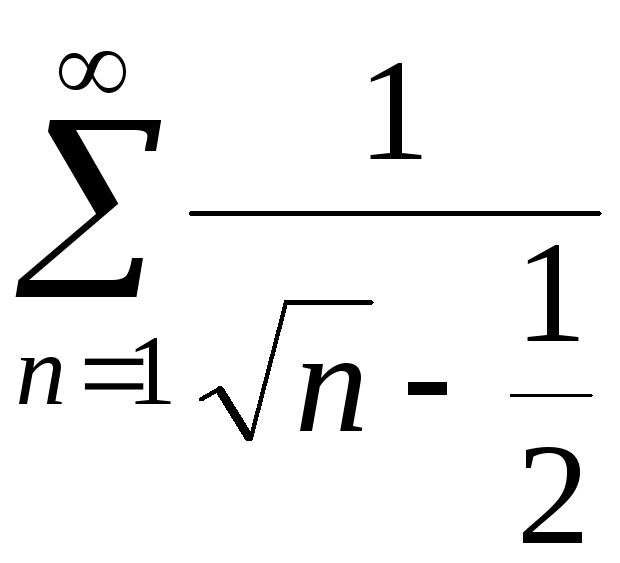 .
Сравним его с рядом
.
Сравним его с рядом![]() ,
который расходится (см. пример на с. 7).
Ввиду неравенства
,
который расходится (см. пример на с. 7).
Ввиду неравенства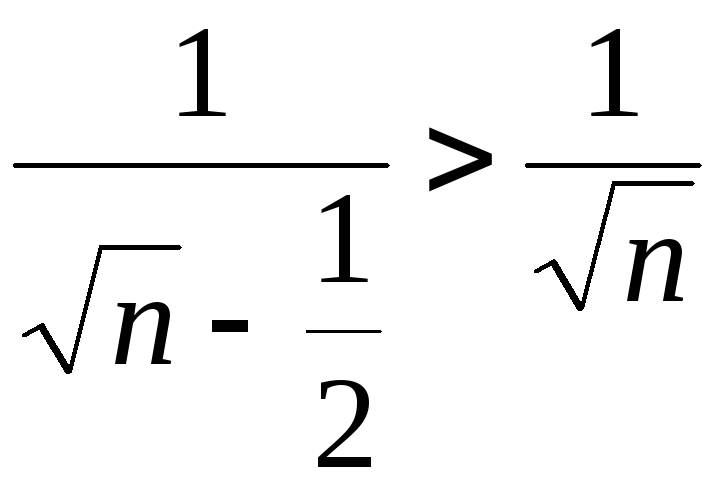 ,
исходный ряд также расходится.
,
исходный ряд также расходится.
Теорема (предельный признак сравнения). Пусть существует конечный предел
![]() ,
,
и ряд (9) сходится. Тогда ряд (8) также сходится.
Доказательство.
Поскольку
![]() ,
то под знаком предела стоит положительная
величина, и по теореме о предельном
переходе в неравенстве
,
то под знаком предела стоит положительная
величина, и по теореме о предельном
переходе в неравенстве![]() .
Зафиксируем
.
Зафиксируем![]() .
Тогда при всех
.
Тогда при всех![]() ,
начиная с некоторого
,
начиная с некоторого![]() :
:
![]() .
.
Поскольку ряд
![]() сходится (п. 1.4), то сходится также ряд
сходится (п. 1.4), то сходится также ряд![]() ;
тогда по предыдущей теореме сходится
ряд
;
тогда по предыдущей теореме сходится
ряд![]() ,
а вместе с ним и ряд
,
а вместе с ним и ряд![]() .
■
.
■
Замечание.
Если в условии теоремы
![]() ,
то
,
то
![]() ,
,
и
тогда из сходимости ряда
![]() следует сходимость ряда
следует сходимость ряда
![]() .
Итак, при
.
Итак, при
![]() ряды(8)
и (9)
сходятся или расходятся одновременно.
ряды(8)
и (9)
сходятся или расходятся одновременно.
Примеры.
1.
Рассмотрим ряд
![]() .
Сравним его со сходящимся рядом
.
Сравним его со сходящимся рядом![]() .
Поскольку
.
Поскольку
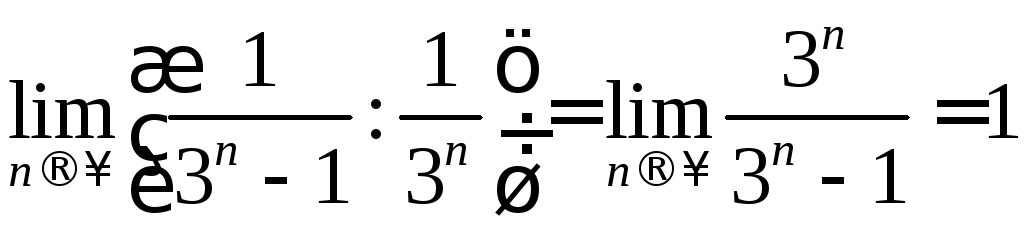 ,
,
то
ряд
![]() сходится.
сходится.
2.
Рассмотрим ряд
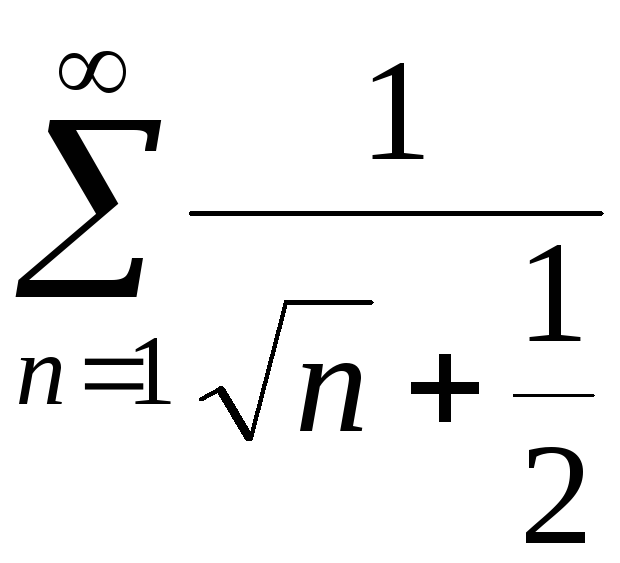 .
Сравним его с расходящимся рядом
.
Сравним его с расходящимся рядом![]() .
Поскольку
.
Поскольку
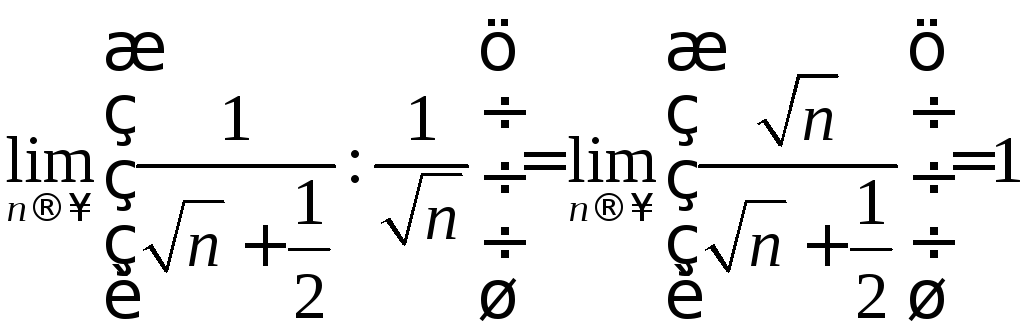 ,
,
то
ряд
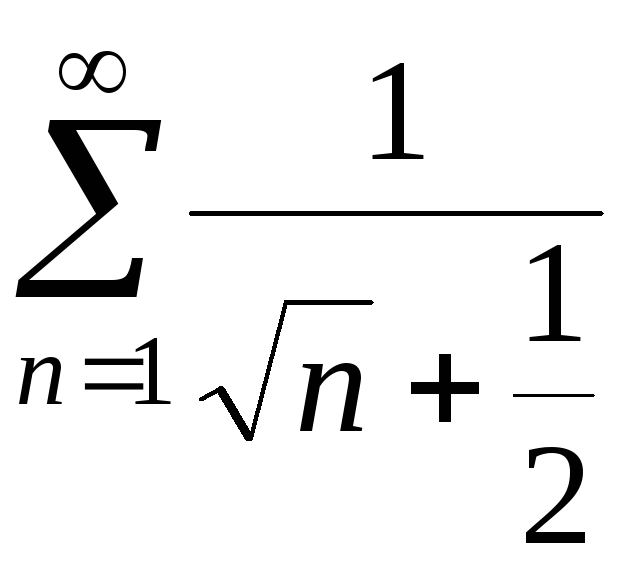 расходится.
расходится.
1.8. Радикальный признак сходимости Коши
Теорема.
Пусть для
ряда
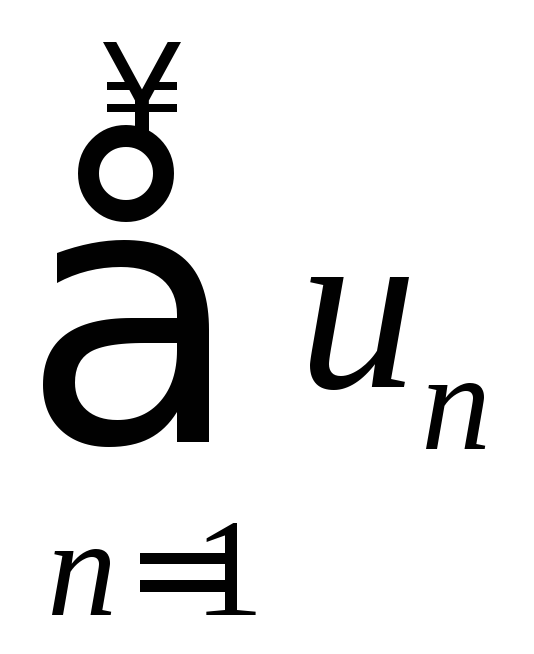 с положительными членами
с положительными членами![]() ,
существует предел
,
существует предел![]() .
Тогда при
.
Тогда при![]() ряд сходится, а при
ряд сходится, а при![]() ряд расходится.
ряд расходится.
Доказательство.
1. Пусть
![]() .
Выберем число
.
Выберем число![]() так, чтобы выполнялось неравенство
так, чтобы выполнялось неравенство![]() .
Тогда существует номер
.
Тогда существует номер![]() такой, что при всех
такой, что при всех![]() выполняется неравенство:
выполняется неравенство:![]() .
Ряд
.
Ряд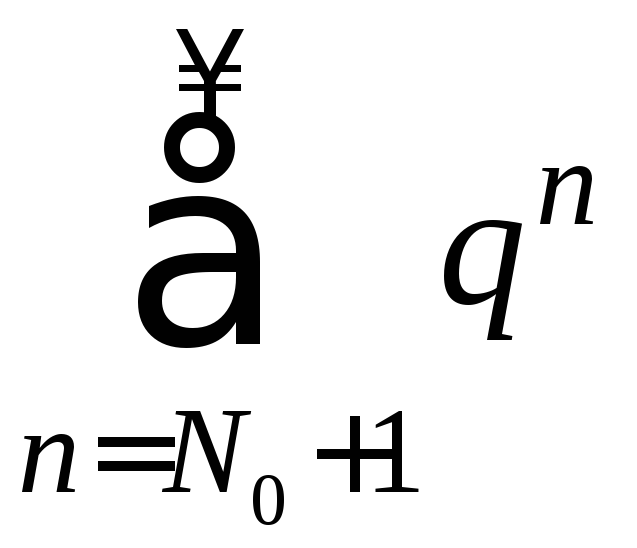 ,
образованный геометрической прогрессией
со знаменателем
,
образованный геометрической прогрессией
со знаменателем![]() ,
сходится (п. 1.3), следовательно, сходится
остаток ряда
,
сходится (п. 1.3), следовательно, сходится
остаток ряда
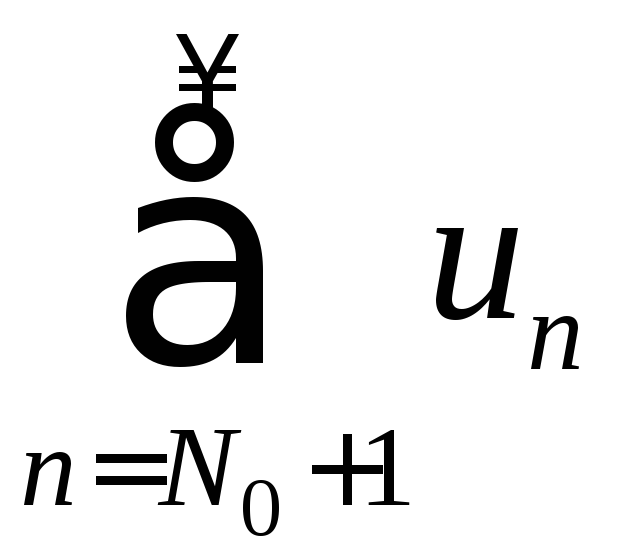 ,
а значит и сам ряд.
,
а значит и сам ряд.
2.
Пусть
![]() .
Тогда существует номер
.
Тогда существует номер![]() такой, что при всех
такой, что при всех![]() выполняется неравенство:
выполняется неравенство:![]() ;
общий член ряда не стремится к нулю,
следовательно, ряд расходится. ■
;
общий член ряда не стремится к нулю,
следовательно, ряд расходится. ■
Замечание.При
![]() «признак не работает»:
существуют примеры как сходящихся, так
и расходящихся рядов с
«признак не работает»:
существуют примеры как сходящихся, так
и расходящихся рядов с
![]() .
.
