2.7. Коэффициенты Тейлора функции.

Если функция является суммой степенного ряда, то из теоремы о почленном дифференцировании (п. 2.4) следует, что она является бесконечно дифференцируемой в интервале сходимости. Однако произвольная бесконечно дифференцируемая в интервалефункция может и не быть в этом интервале суммой степенного ряда.

Теорема.Пусть функция является суммой степенного ряда(20)в окрестности точки :

. (29)

Тогда коэффициенты этого ряда определены однозначно и имеют вид:

. (30)

(для сохранения единства обозначений полагают ).

Доказательство.Полагая в равенстве (29), получаем.

Продифференцируем равенство (29) (причем степенной ряд в левой части — почленно):

(31)

Полагая здесь , получаем.

Продифференцируем равенство (31): .(32)

Полагая здесь , получаем:

.

Продифференцируем равенство (32):

.

Полагая здесь , получаем:

, и так далее.

После -го дифференцирования получаем при:

. ■

Определение.Пусть функциябесконечно дифференцируема в окрестности точки.Коэффициентами Тейлорафункциив точкеназываются числа .

2.8. Ряд Тейлора функции

Из последней теоремы следует, что если функция является суммой степенного ряда по степеням , то коэффициенты этого ряда обязательно являются коэффициентами Тейлора.

Определение.Пусть функцияявляется бесконечно дифференцируемой в окрестности точки.Рядом Тейлораэтой функции называется степенной ряд по степеням, коэффициентами которого являются коэффициенты Тейлора:

. (33)

Замечание.Если заранее не известно, что функцияраскладывается в степенной ряд, то формально составленный ряд Тейлора этой функции может оказаться расходящимся, либо сходящимся, но с суммой, отличной от.

Определение.Рядом Маклоренафункцииназывается ее ряд Тейлора в окрестности нулевой точки (ряд по степеням):

.

2.9. Остаточный член ряда Тейлора

Пусть функция бесконечно дифференцируема в окрестности точки, и — ее ряд Тейлора. Обозначим через частичную сумму ряда:

— функция переменной .

Сходимость ряда Тейлора в терминах остаточного члена

Определение.Остаточным членом ряда Тейлораназывается функция.

Остаточный член выражает погрешность, допускаемую при замене значения функции значением частичной суммы ее ряда Тейлора.

Из определения остаточного члена вытекает равенство:

.

Сходимость ряда Тейлора в точке к, то есть равенство

,

означает, согласно определению сходимости ряда, что

.

Итак, для сходимости ряда Тейлора в точке кнеобходимо и достаточно, чтобы в этой точке остаточный член стремился к нулю.

Теорема (о виде остаточного члена).Если функция бесконечно дифференцируема в окрестности точки, то при каждом фиксированном значениидля всехиз этой окрестности справедлива формула:

,(34)

где промежуточная точка зависит оти лежит междуи.

Замечание.В формуле (34) остаточный член имеет вид-го члена ряда Тейлора с той лишь разницей, что производнаявычисляется не в самой точке , а в некоторой промежуточной точке.

Доказательство.Зафиксируем точкуиз указанной окрестности и положим

.

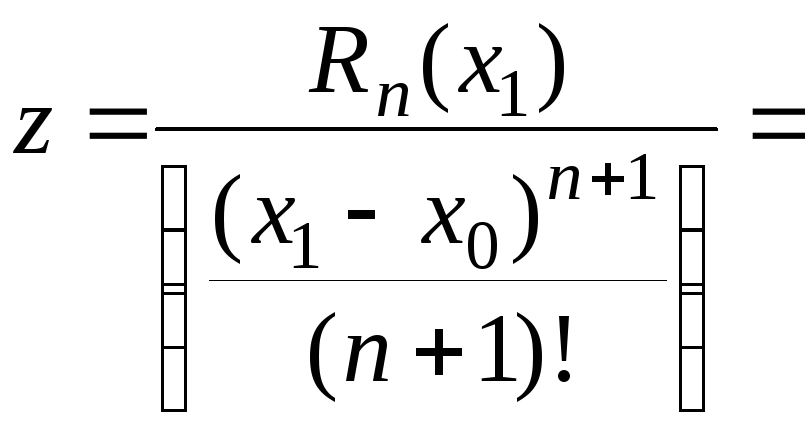
(— постоянное число). Нужно убедиться, что при некоторомвыполняется равносильное (34) равенство:.

Имея ввиду применение теоремы Ролля, введем функцию

,

которая непрерывна на отрезке между ии дифференцируема в интервале с этими же границами: нетрудно убедиться —проведите необходимые выкладки — что

, (*)

, и .

По теореме Ролля существует промежуточная точка , в которой. Тогда из (*) получаем. ■

Определение.Формула (34) носит названиеформулы остаточного члена в форме Лагранжа.