The G3 Theory and Its Variants |
81 |
The increase in the mean absolute deviation for all three methods is primarily due to large errors in the calculated enthalpies of formation of some of the non-hydrogen species in the expanded G3/99 test set. This is similar to the results for the G3 methods based on the higherlevel correction per electron pair. The G3S mean absolute deviation of 3.37 kcal/mol for the 13 non-hydrogen species in the G3-3 subset is more than twice that of 1.60 kcal/mol for the 34 non-hydrogens in the G2/97 set. Similar increases in the mean absolute deviations occur for the G3S(MP3) and G3S(MP2) theories.
The mean absolute deviation of G3S for the G3-3 subset of larger molecules is 1.43 kcal/mol compared to 1.30 kcal/mol for G3. The larger increase for G3S method suggests that the scaling approach based on six parameters may not work as well on molecules outside the parameterization test set as does an approach based on the four-parameter higherlevel correction. For example, the deviation of G3S standard enthalpy of formation of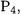 
a molecule with unusual bonding, amounts to 10 kcal/mol. If nine instead of six scaling parameters are used in G3S, the mean absolute deviation is 1.29 kcal/mol for the new subset, about the same as G3 theory. This suggests that a larger number of parameters may be needed in the scaling approach to make it as accurate as its HLC-based counterpart, although additional assessments are needed to confirm this suspicion.
5.G3X THEORY
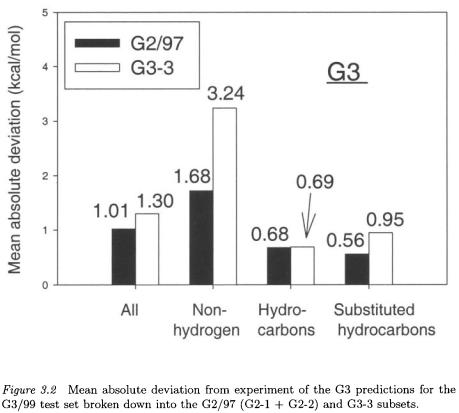
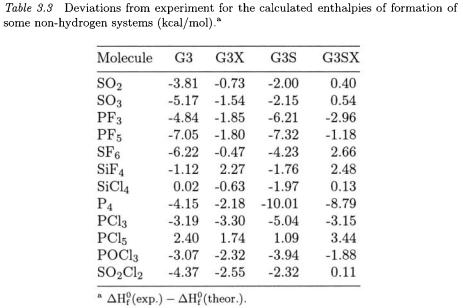
A new family of G3 methods, referred to as G3X (G3 eXtended) has been developed recently [30] to improve the accuracy of the results for some of the larger molecules included in the G3/99 test set. In the assessment of G3 theory [21] on the G3/99 test set, the mean absolute deviation from experiment (1.07 kcal/mol) was slightly larger than the corresponding value of 1.01 kcal/mol found originally for the smaller G2/97 test set. Significantly larger deviations were, however, found for the larger non-hydrogen systems containing second-row atoms (Fig. 3.2).
The larger non-hydrogen systems have deviations (3.24 kcal/mol) almost twice as large as those included in the smaller G2/97 test set (1.68 kcal/mol). In particular, hypervalent molecules such as 
and 
have deviations ranging from 5 to 7 kcal/mol. Part of the source of errors in the G3 results for the non-hydrogen species was traced to the MP2/6-31G(d) geometries used in the single-point energy calculations. Use of experimental geometries instead of the MP2/6-31G(d) ones in a small subset of non-hydrogen molecules reduced the deviations in those
82 |
Chapter 3 |
species, but they still remained as large as 3 - 4 kcal/mol. The remainder of the error was attributed to basis set deficiencies.
Three modifications have been included in the G3X method to alleviate these deficiencies:
1.B3LYP/6-31G(2df,p) geometries are used in place of the MP2(fu)/ 6-31G(d) geometries. These new geometries have significantly smaller deviations from experiment than their original counterparts. For example, the deviation from experiment in the bond
lengths for a subset of seven representative molecules (
and 
) decreased from 0.027 Å [MP2(fu)/6-
31G(d)] to 0.011 Å [B3LYP/6-31G(2df,p)].
2.B3LYP/6-31G(2df,p) zero-point energies (scaled by 0.9854) are used in place of the HF/6-31G(d) zero-point energies (scaled by 0.8929). The former scale factor is derived from fitting the set of zero-point energies compiled by Scott and Radom [57]. The small correction suggests that the B3LYP/6-31G(2df,p) level of theory is
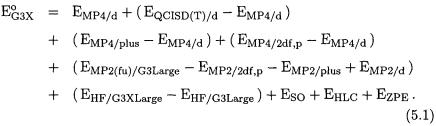
The G3 Theory and Its Variants |
83 |
accurate for zero-point energies as well as geometries. This choice differs in two ways from that of the original G3 procedure. First of all, in G3 theory the zero-point energies and geometries are calculated at two different levels of theory, namely HF/6-31G(d) and MP2(fu)/6-31G(d). Secondly, the HF/6-31G(d) scale factor was based on fitting of experimental vibrational frequencies rather than zero-point energies. Thus, the new procedure for calculating zero-point energies in G3X theory is more consistent than that employed in G3 theory.
3.The G3Large basis set for second-row atoms is augmented at the Hartree-Fock level with g valence polarization functions [31]. Significant improvement in the calculated atomization energies were found for some representative molecules. For example, the addition of a single set of g functions to the second-row atoms (Si - Cl)
increases the binding in 
and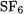 
by 3.6, 5.1, and 5.5 kcal/mol, respectively, at the Hartree-Fock level. The increase is much smaller for similar molecules containing chlorine. Addition of more polarization functions (2g,2gh) on the second-row atoms results in substantially smaller changes in the atomization energies
[31].Thus, in G3X theory, a single set of g polarization functions (7 pure functions) is added to the second-row G3Large basis set at the HF level. The g exponents for Al - Cl are taken from Dunning’s correlation consistent cc-pVQZ basis set [58] (Al: 0.357, Si: 0.461,
P:0.597, S: 0.683, Cl: 0.827, and Ar: 1.007). No g functions are used for Na or Mg. This new basis set is referred to as G3XLarge.
It should be noted that similar basis set deficiencies occur also at correlated levels. Correcting such deficiencies at the correlated level is more difficult due to their slow convergence, though the HLC parameters offer partial remedy.
The total G3X energy incorporating these three features is given by the equation
Eq. (5.1) is the same as for G3 theory except for the addition of the Hartree-Fock term. This term extends the HF/G3Large energy, which
84 |
Chapter 3 |
is part of the MP2(fu)/G3Large energy, to the G3XLarge basis set. As in G3 theory, all correlation calculations (except for MP2/G3Large) are done with a frozen core.
As discussed earlier, the single-point energies in Eq. (5.1) are calculated at B3LYP/6-31G(2df,p) geometries, and the zero-point energies and thermal corrections are obtained from scaled frequencies computed at the same level of theory. The higher-level correction (HLC) parameters were obtained by fitting to the full G3/99 test set. Fitting of the HLC parameters to the smaller G2/97 test set gives nearly the same values for the four parameters, indicating that there is little sensitivity to the increase in the data set size. The G3X method takes about 10 - 15 % more time than G3 due to the B3LYP/6-3lG(2df,p) frequency calculation.
G3X theory gives significantly better agreement with experiment for the G3/99 test set of 376 energies. Overall, the mean absolute deviation from experiment decreases from 1.07 kcal/mol (G3) to 0.95 kcal/mol (G3X). The mean absolute deviation for the 222 enthalpies of formation decreases from 1.05 kcal/mol (G3) to 0.88 kcal/mol (G3X). The improvement is largely due to the non-hydrogen systems for which the mean absolute deviation decreases from 2.11 to 1.49 kcal/mol. The increased accuracy of G3X is due to both the use of a new geometry and the larger Hartree-Fock basis set. The latter is especially important for hypervalent molecules.
The G3 Theory and Its Variants |
85 |
Unlike in the case of G3 theory, there is very little degradation in G3X theory for larger molecules. The overall mean absolute deviation from experiment is nearly the same for the larger G3/99 test set (0.95 kcal/mol) as it is for its smaller G2/97 counterpart (0.96 kcal/mol). Similarly, the mean absolute deviation from experiment for enthalpies is nearly the same for the larger G3/99 test set (0.88 kcal/mol) as it is for the smaller G2/97 test set (0.86 kcal/mol). It is also important to note that this result is not dependent on the data set used to obtain the HLC parameters since both sets give essentially the same values.
Some examples of the changes observed upon going from G3 to G3X theory for selected non-hydrogen systems are shown in Table 3.3. Significant improvements are seen in most cases, though errors in the range of 2 or 3 kcal/mol remain in some molecules. The reliability of the G3X method is illustrated by the fact that only one molecule 
has an error of more than 4 kcal/mol (note that the experimental enthalpy of formation of 
has been recently called into question).
The three new features of G3X theory can also be easily included in the G3(MP3) and G3(MP2) methods. The resulting theories are referred to as G3X(MP3) and G3X(MP2), respectively. The G3X(MP3) energy is given by
Eqs. (5.2) and (5.3) are the same as for G3(MP3) and G3(MP2) theories, except for the addition of the Hartree-Fock (HF) term. As in the case of G3X, this term extends the HF energy to the G3XLarge basis set. Again, the single-point energies in Eqs. (5.2) and (5.3) are calculated at the B3LYP/6-31G(2df,p) geometries and the zero-point energies are
86 |
Chapter 3 |
computed from scaled B3LYP/6-31G(2df,p) frequencies. The higherlevel correction (HLC) parameters were obtained by fitting to the G3/99 test set.
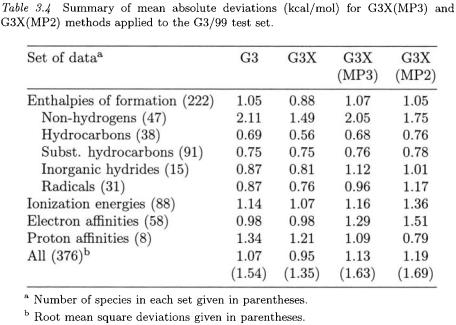
Summaries of G3X(MP3) and G3X(MP2) mean absolute deviations from experiment for the G3/99 test set of 376 energies are given in Table 3.4. The overall mean absolute deviations for G3X(MP3) and G3X(MP2) theories are 1.13 and 1.19 kcal/mol, respectively. These are improvements over G3(MP3) and G3(MP2), which have mean absolute deviations of 1.27 and 1.31 kcal/mol, respectively, for the same set of energies. For enthalpies of formation, the mean absolute deviations decrease from 1.29 to 1.07 kcal/mol [G3X(MP3)] and from 1.22 to 1.05 kcal/mol [G3X(MP2)]. Much of the improvement in enthalpies is due to non-hydrogen molecules, although other types of species also improve slightly or stay the same. The G3X(MP3) and G3X(MP2) methods save considerable computational time and have a reasonable accuracy. The ratio of the computational costs for G3X, G3X(MP3), and G3X(MP2) theories is approximately 5:2:1 for a molecule such as benzene.
The three new features of G3X theory can also be included in the G3S method. The resulting theory is referred to as G3SX and the energy is given by
The G3 Theory and Its Variants |
87 |
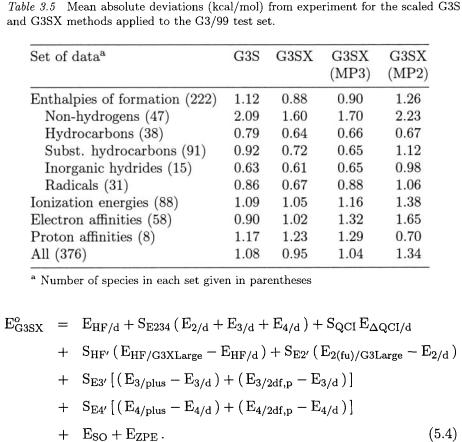
Eq. (5.4) is identical to that of the corresponding G3S method, except for the use of the G3XLarge basis set in the Hartree-Fock term instead of the G3Large basis. Also, the single-point energies are calculated at the B3LYP/6-31G(2df,p) geometries and the zero-point energies are obtained from scaled B3LYP/6-31G(2df,p) frequencies. The scaling parameters were obtained by fitting to the G3/99 test set. G3SX has six parameters, one for the Hartree-Fock energy extension and five for the correlation terms. Note that ideally the parameters should be close to one; however, the 
scale factor is 0.66, which may cause problems in some cases (see below). In a similar manner, the methods based on reduced perturbation orders, namely G3SX(MP3) and G3SX(MP2), are derived by adding the three new features to the G3S(MP3) and G3S(MP2) methods, respectively.
A summary of G3SX mean absolute deviations from experiment for the G3/99 test set of 376 energies is given in Table 3.5. Overall,