Задачи для самостоятельного решения

Группа А

Решить систему (1-8)

1. (Ответ: .)

2. (Ответ: .)

3. (Ответ: .)

4. (Ответ: .)

5. (Ответ: .)

6. (Ответ: .)

7. (Ответ: , .)

8. 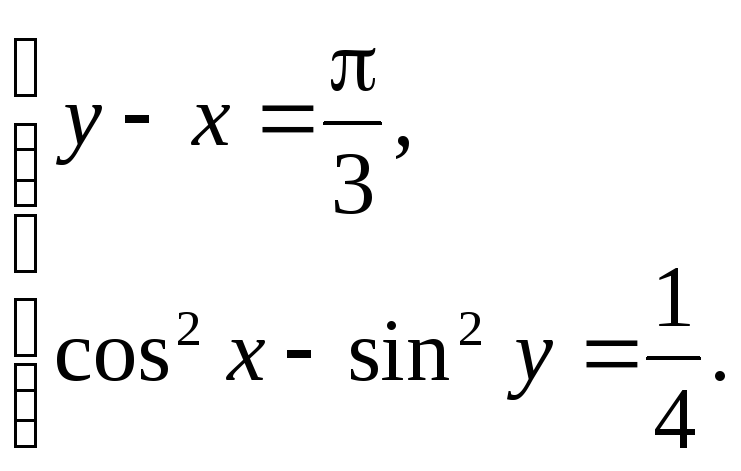(Ответ: ; .)

Группа B

Решить систему (1-16)

1. (Ответ: .)

2. 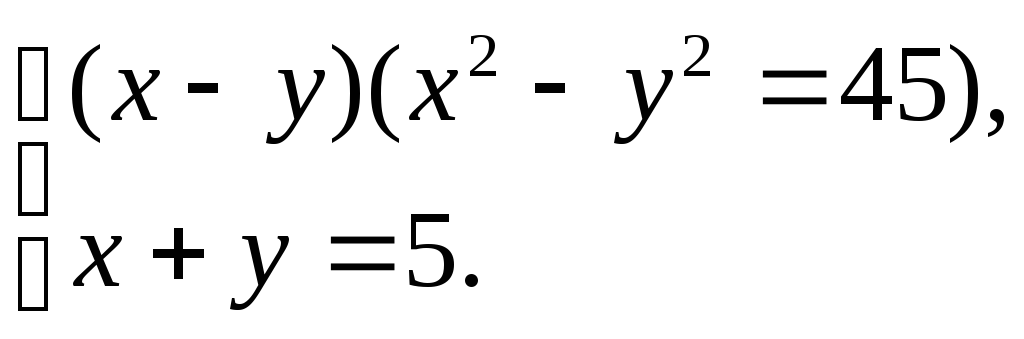(Ответ: .)

3. (Ответ: .)

4. 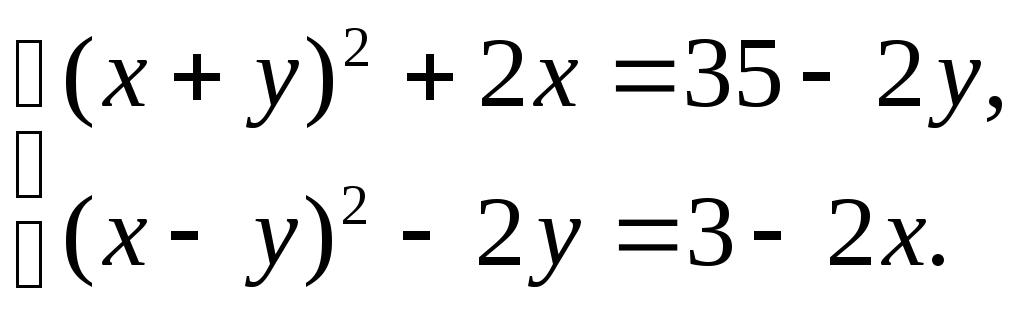(Ответ: ,.)

5. 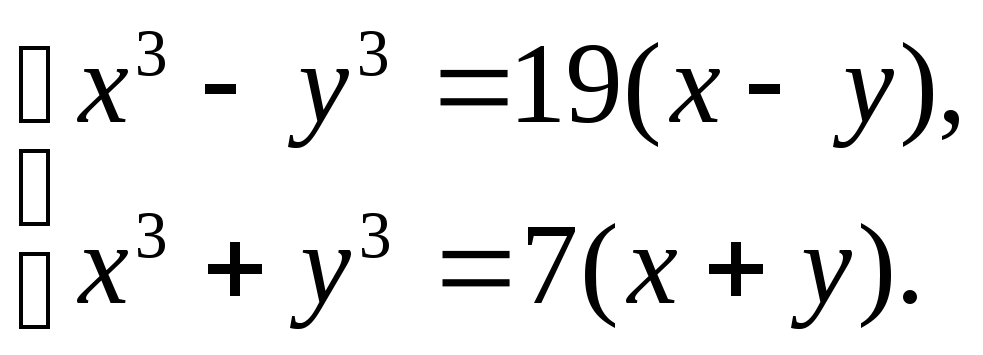(Ответ: .)

6. (Ответ: .)

7. (Ответ: .)

8. (Ответ: .)

9. (Ответ: .)

10. 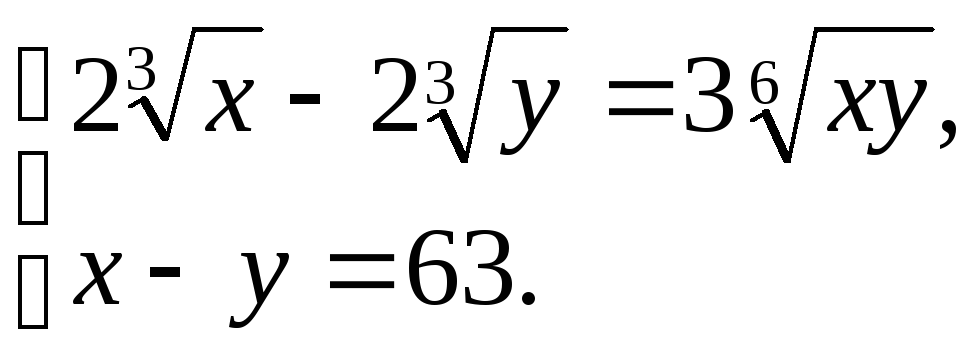(Ответ: .)

11. (Ответ: .)

12. (Ответ: .)

13. 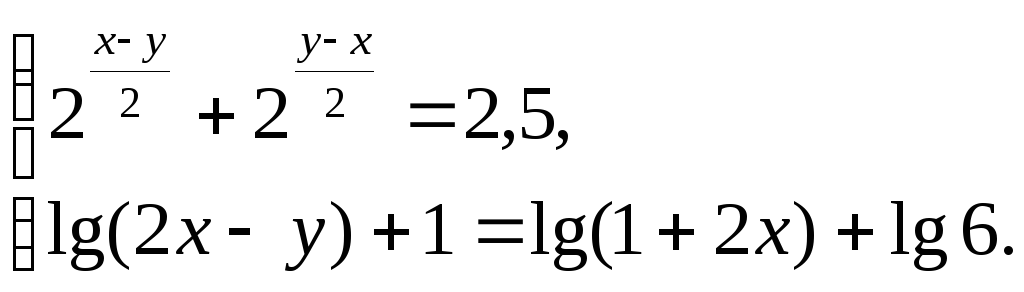(Ответ: .)

14.

(Ответ: ;

, .)

15. (Ответ: , .)

16.

(Ответ: ,, .)

Группа С

Решить систему (1-9)

1. (Ответ: .)

2.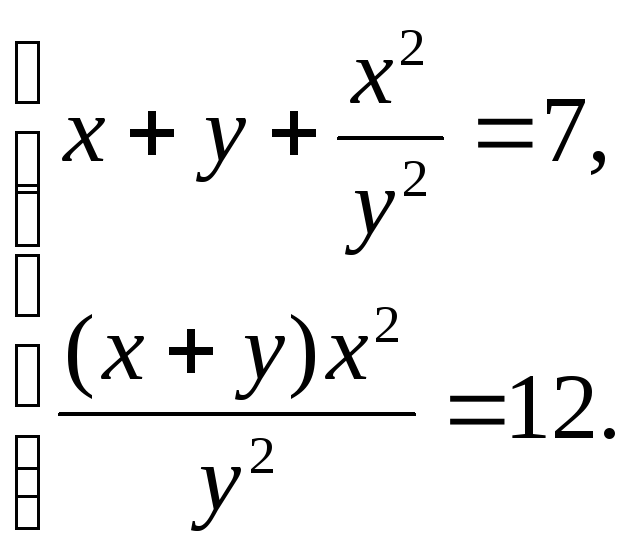 (Ответ:.)

3. (Ответ: ,.)

4. 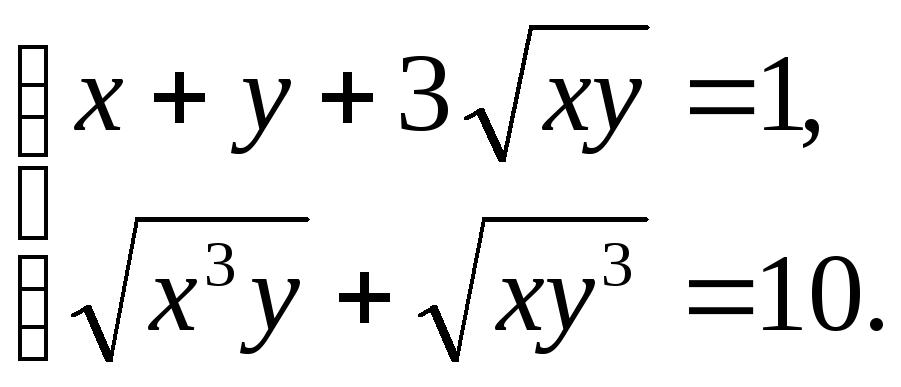(Ответ: .)

5. (Ответ: .)

6. (Ответ: .)

7. (Ответ: .)

8. 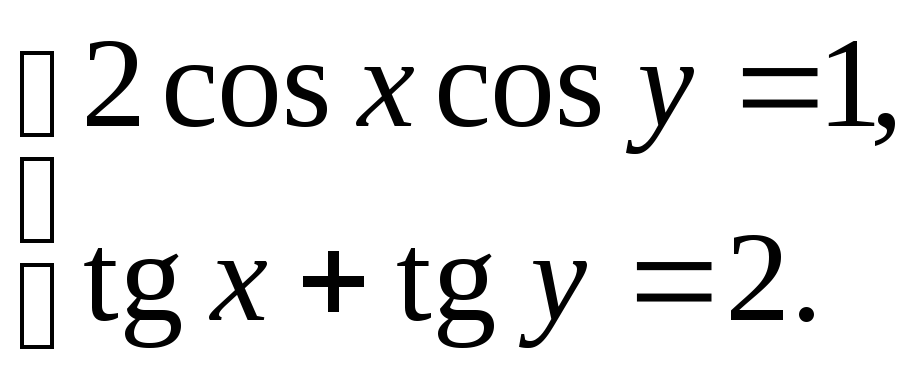(Ответ: , .)

9. (Ответ: , .)

10. Дифференциальное исчисление функции одной переменной

10.1. Понятие производной функции.

Правила дифференцирования.

Определение 10.1. Производной функции в точкеназывается предел отношения приращения функции в этой точкек приращению аргументапри(если такой предел существует):

.

Геометрический смысл производной

Производная в точке равна угловому коэффициенту касательной к графику функциив этой точке(рис. 10.1).

рис. 10.1.

Уравнение касательной к графику функции в точке:

.

Правила нахождения производной

Если у функций исуществуют производные, то

, где

Производная сложной функции

Если и существуют производныеи, то, где индексыиуказывают, по какому аргументу берутся производные.

Производные элементарных функций

№	Функция		№	Функция
1			11
2			12
3			13
4			14
5			15
6			16
7			17
8			18
9			19
10			20

Пример 10.1. Найти производную функции .

Решение. Применяя формулы и правила дифференцирования, получаем:

.

Ответ: .

Пример 10.2. Найти производную функции .

Решение. .

Ответ: .

Пример 10.3. Найти производную функции .

Решение. .

.

Ответ: .

Пример 10.4. Найти производную функции .

Решение.

.

Ответ: .

Пример 10.5. Найти производную функции .

Решение. Положим , тогда. Согласно правилу дифференцирования сложной функции, имеем

.

Ответ: .

Пример 10.6. Найти производную функции .

Решение. .

Ответ: .

Пример 10.7. Найти производную функции .

Решение. .

Ответ: .

Пример 10.8. Найти производную функции .

Решение. .

Ответ: .

Пример 10.9. Найти производную функции .

Решение. =

.

Ответ: .

Пример 10.10. Найти производную функции .

Решение. Преобразуем данную функцию:

,

тогда получим

,

или

.

Ответ: .

10.2. Приложения производной Исследование функции с помощью производной.

Теорема 10.1. (Достаточное условие возрастания функции). Если в каждой точке интервала производная функции, то функциявозрастает на этом интервале.

Теорема 10.2. (Достаточное условие убывания функции). Если в каждой точке интервала производная функции , то функция убывает на этом интервале.

Определение 10.2. Точка называетсяточкой минимума функции ,если для всех из некоторой окрестности точкивыполнено неравенство

.

Определение 10.3. Точка называетсяточкой максимума функции ,если для всех из некоторой окрестности точкивыполнено неравенство.

Замечание 10.1. Для точек максимума и минимума функции принято общее название – точки экстремума функции. Значения в этих точках называют соответственно максимумами () и минимумами () функции.

Теорема 10.3. (Необходимое условие экстремума функции). Для того чтобы функция имела экстремум в точке, необходимо, чтобы производная в этой точке равнялась нулю() или не существовала.

Точки, в которых выполнено необходимое условие экстремума, то есть производная равна нулю или не существует, называются критическими точками. Отметим, что эти точки должны входить в область определения функции.

Таким образом, если в какой-то точке имеется экстремум, то эта точка критическая. Однако, обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума.

Теорема 10.4. (Достаточное условие экстремума функции). Если при переходе через точку производная дифференцируемой функциименяет свой знак с плюса на минус, то точкаесть точка максимума функции, а если с минуса на плюс, то точка минимума.

Схема нахождения интервалов монотонности и экстремумов функции

1. Найти область определения функции.

2. Найти производную функции.

3. Найти критические точки.

4. В каждом из интервалов, а которые область определения разбивается критическими точками, определить знак производной и характер изменения функции.

5. Относительно каждой критической точки определить, является ли она точкой максимума, минимума или не является точкой экстремума.

6. Записать результат исследования функции: промежутки монотонности и экстремумы.