9.3. Системы иррациональных уравнений

Пример 9.11. Решить систему

Решение.

Сделаем в первом уравнение системы замену: , тогда

Делая обратную замену, получаем

1) 2)

Ответ: ,.

Пример 9.12. Решить систему

Решение. Подставим в первое уравнение системы:

Ответ: .

Пример 9.13. Решить систему

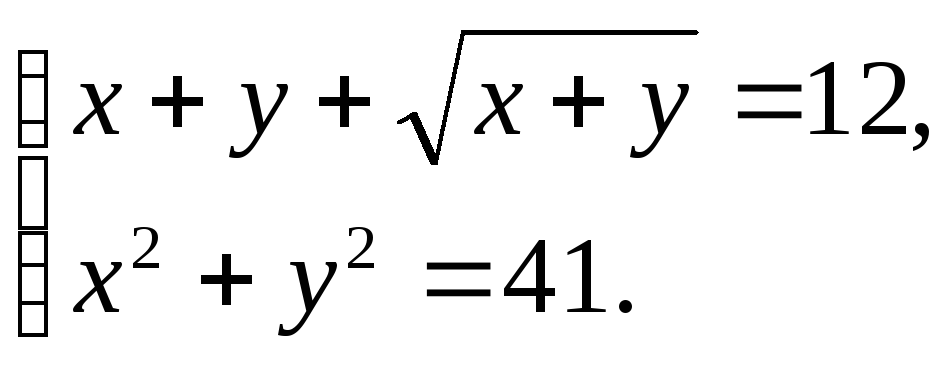
Решение. Обозначим ,, тогда первое уравнение равносильно системе:

тогда исходную систему можно переписать в виде:

Ответ: .

Пример 9.14. Решить систему

Решение. Обозначим ,, тогда первое уравнение системы можно переписать в виде

Переходя к исходным переменным, получаем

1)

2)

Ответ: .

Пример 9.15. Решить систему

Решение. Учитывая, что ,, возведем обе части первого уравнения системы в квадрат, получим:

Ответ: .

9.4. Системы показательных и логарифмических уравнений

Пример 9.16. Решить систему

Решение. Область определения системы описывается условиями:

Сделаем в первом уравнении системы замену ,, тогда получим

,

или, переходя к исходным переменным,

.

Подставим полученное выражение для неизвестной во второе уравнение системы:

,

откуда

Соответствующие ;. Проверкой убеждаемся, что паране входит в область определения системы, то есть является посторонним решением.

Ответ: .

Пример 9.17. Решить систему

Решение. Область определения системы:

Используя свойства логарифмов, преобразуем исходную систему:

Делая проверку, получаем, что - постороннее решение.

Ответ: .

Пример 9.18. Решить систему

Решение.

Ответ: .

Пример 9.19. Решить систему

Решение. Область определения системы ,. Прологарифмируем первое и второе уравнения системы по основаниюи проведем преобразования системы на ОДЗ:

1) 2)

Ответ: .

Пример 9.20. Решить систему

Решение. Область определения системы . Преобразуем исходную систему:откуда, учитывая, что,

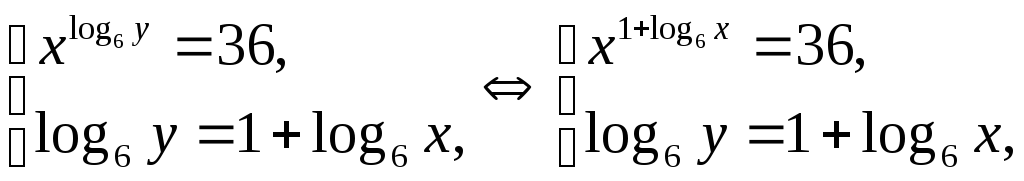
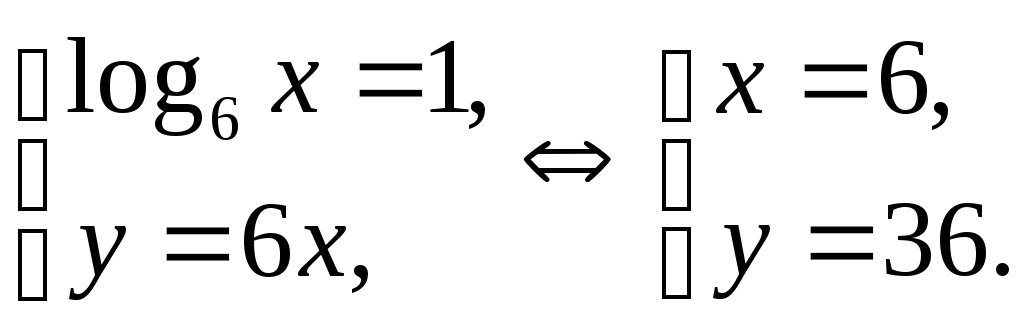
прологарифмируем первое уравнение системы по основанию 6 и потенцируем второе, тогда

1) 2)

Ответ: .

Пример 9.21. Решить систему

Решение. Область определения системы Проведем преобразования системы на ОДЗ:

Рассмотрим второе уравнение системы. Введем замену: ,, тогда

делая обратную замену, имеем

,

или в итоге . Так как, преобразуем выражения для области определения системы

Следовательно, решениями являются и.

Ответ: .

9.5. Системы тригонометрических уравнений

Пример 9.22. Решить систему

Решение.

Сложим и вычтем уравнения системы:

.

Ответ: , .

Пример 9.23. Решить систему

Решение. Преобразуем первое уравнение системы:

,

тогда

1)

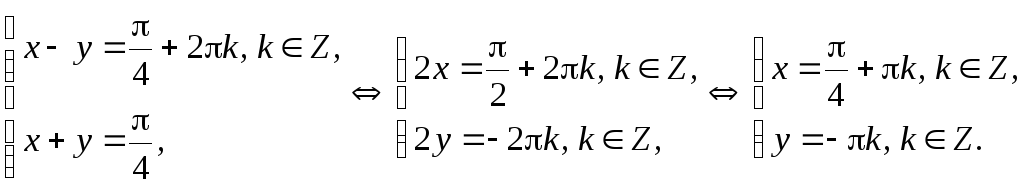
2)

Ответ: ,, .

Пример 9.24. Решить систему

Решение. Сделаем замену: ,,,, тогда исходная система примет вид:Умножим первое уравнение системы на 3 и прибавим ко второму:

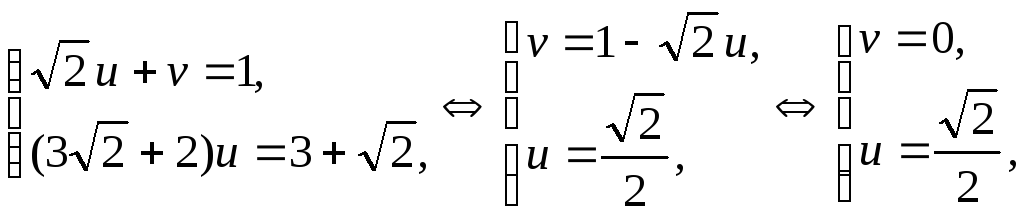
возвращаясь к исходным переменным, имеем

.

Ответ: , .

Пример 9.25. Решить систему

Решение. Сложим и вычтем уравнения системы, тогда

.

1) ,

2) .

Ответ: ;, .

Пример 9.26. Решить систему

Решение. Возведем обе части уравнений системы в квадрат и сложим их:

.

Подставим полученное выражение для неизвестной в исходную систему, тогда получаем:

Возможны следующие случаи.

1) Если , , то, учитывая, что , имеем

откуда .

2) Аналогично, если , , то,

откуда .

Ответ: ;, .