
- •ВВЕДЕНИЕ
- •ГЛАВА 1. ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ
- •ВЫРАЖЕНИЙ
- •1.1. Многочлены
- •1.1.1. Формулы сокращенного умножения
- •1.1.2. Операции над многочленами одной переменной
- •1.1.3. Корни многочлена
- •1.2. Разложение многочленов на множители
- •1.2.1. Вынесение общего множителя за скобку
- •1.2.2. Способ группировки
- •1.2.3. Использование тождеств сокращенного умножения
- •1.2.4. Разложение многочлена на множители с помощью его корней
- •1.3. Выделение полного квадрата
- •1.4. Многочлены от нескольких переменных
- •1.5. Свойства степени с любым рациональным показателем
- •1.6. Упражнения для самостоятельного выполнения
- •ГЛАВА 2. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА.
- •МЕТОД ИНТЕРВАЛОВ
- •2.1. Задачи для самостоятельного решения
- •ГЛАВА 3. НЕРАВЕНСТВА С МОДУЛЕМ
- •3.1. Задачи для самостоятельного решения
- •ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
- •4.1. Линейные и дробно-линейные функции
- •4.1.1. Прямая пропорциональность
- •4.1.2. Линейная функция
- •4.1.3. Обратная пропорциональность
- •4.2. Квадратичная функция
- •4.3. Степенная функция
- •4.4. Показательная функция
- •4.5. Логарифмическая функция
- •4.6. Тригонометрические функции
- •4.7. Обратные тригонометрические функции
- •4.8. Преобразования графиков функций
- •4.9. Задания для самостоятельного решения
- •ГЛАВА 5. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ
- •5.1. Основные понятия и обозначения
- •5.3. Построение кривых в полярной системе координат
- •5.4. Задания для самостоятельной работы в аудитории
- •ГЛАВА 6. ЛОГАРИФМЫ
- •6.1. Основные свойства логарифмов. Преобразование выражений,
- •содержащих логарифмы
- •6.1.1. Задания для самостоятельного решения
- •6.2. Простейшие логарифмические уравнения и неравенства
- •6.2.1. Задания для самостоятельного решения
- •7.1. Формулы приведения
- •7.2. Основные тригонометрические формулы
- •7.3. Преобразование выражений
- •7.4. Простейшие тригонометрические уравнения
- •7.5. Простейшие тригонометрические неравенства
- •7.6. Задания для самостоятельного решения
- •ГЛАВА 8. КОМПЛЕКСНЫЕ ЧИСЛА
- •8.1. Основные понятия. Алгебраическая форма комплексного числа
- •8.2. Арифметические операции над комплексными числами,
- •заданными в алгебраической форме
- •8.3. Комплексные числа в тригонометрической форме
- •8.3.1. Тригонометрическая форма комплексного числа
- •8.3.2. Действия над комплексными числами в тригонометрической форме
- •8.4. Показательная форма комплексного числа
- •8.5. Задания для самостоятельной работы
- •ГЛАВА 9. ОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКОВ
- •9.1. Понятие определителей второго и третьего порядков
- •9.2. Правила действий над определителями
- •9.3. Задания для самостоятельной работы
- •ГЛАВА 10. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- •10.1. Основные понятия и определения
- •10.2. Линейные операции над векторами
- •10.2.1. Сложение векторов
- •10.2.2. Вычитание векторов
- •10.2.3. Умножение вектора на число
- •10.2.4. Проекция вектора на ось
- •10.2.5. Координаты вектора
- •10.2.6. Направляющие косинусы вектора
- •10.3. Скалярное произведение векторов
- •10.3.1. Свойства скалярного произведения
- •10.4. Векторное произведение векторов
- •10.4.1. Свойства векторного произведения векторов
- •10.5. Смешанное произведение векторов
- •10.5.1. Свойства смешанного произведения
- •10.6. Задания для самостоятельной работы
- •ГЛАВА 11 ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- •11.1. Основные понятия и определения
- •11.1.1. Основные правила дифференцирования
- •11.1.2. Производные основных элементарных функций
- •11.1.3. Производная сложной функции
- •11.2. Задания для самостоятельной работы
- •СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
4.1. Линейные и дробно-линейные функции
4.1.1. Прямая пропорциональность
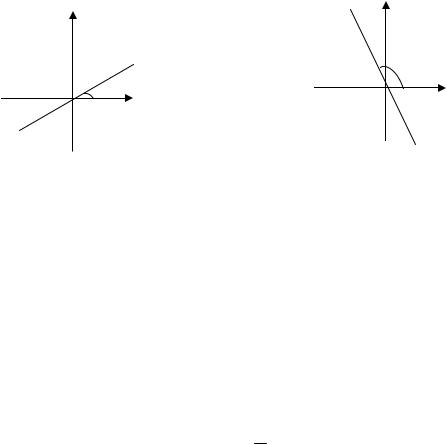
Функция y kx , где k действительное число, k 0 , называется пря-
мой пропорциональностью. Основные свойства:
1.Область определения – R ;
2.Область значений – R ;
3.Функция нечетная;
4.Если x 0 , то y 0 ;
5.Если k 0 , то функция возрастает на множестве (рис.4.1, а);
6.Если k 0, то функция убывает на множестве (рис.4.1, б);
7.График прямой пропорциональности – прямая, которая проходит через
начало координат.
y kx |
y |
y |
|
||
|
|
|
k 0 |
|
|
k tg |
|
|
|
|
x |
|
x |
а |
б |
Рис.4.1
4.1.2. Линейная функция
Функция y kx b , где k R ,b R , называется линейной функцией. Основные свойства:
1.Область определения – R ;
2.Область значений – R , если k 0 ; b , если k 0;
3.Если k 0 , b 0 , то функция ни четная, ни нечетная; если k 0 – функция четная; если b 0 ,k 0 – нечетная; если k 0, b 0 – и четная, и нечетная;
4. Если x 0 , то y b ; если x b , функция y 0 ; k
25
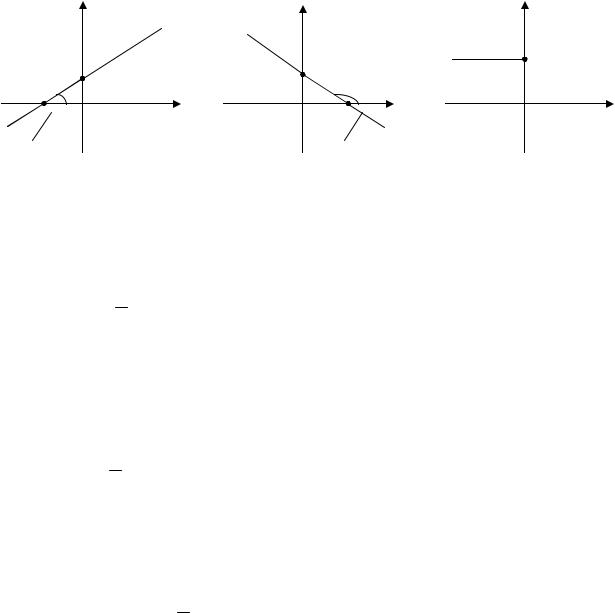
5. Если k 0 , то функция возрастает на множестве R (рис. 4.2, а); если k 0 , то функция убывает на множестве R (рис. 4.2, б); если k 0 , то функция постоянна, y b (рис.4.2, в);
6. График линейной функции – прямая, образующая с осью абсцисс угол
, тангенс которого равен k .
y |
y kx b |
y |
|
|
y |
||
|
|
|
|
|
|
||
|
|
y kx b |
|
|
b |
||
|
|
|
|
|
|||
b |
x |
b |
|
x |
|
|
x |
|
|
|
|||||
|
|
|
|||||
b 0 |
|
0 |
b |
|
0 |
|
|
k |
|
|
k |
|
|
|
|
|
k tg 0 |
|
|
k tg 0 |
|
k tg 0 |
|
а |
|
б |
|
|
|
в |
|
|
|
Рис. 4.2 |
|
|
|
|
|
4.1.3. Обратная пропорциональность
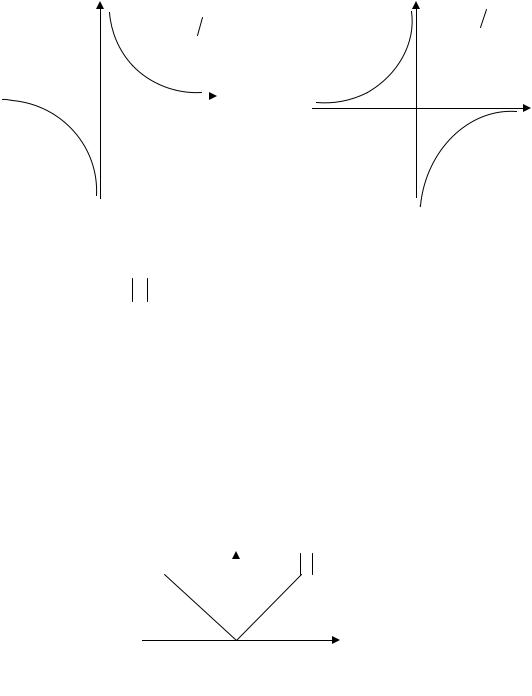
Функция y k , где k R , k 0 , называется обратной пропорциональ- x
ностью.
Основные свойства:
1.Область определения – ( ;0) (0; ) ;
2.Область значений –( ;0),(0; ) ;
3.Функция y k нечетная;
x
4. Если k 0 , то на интервале ( ;0) функция убывает, на интервале
(0; ) – также убывает (рис. 4.3, а). Если k 0, то на интервалах
( ;0),(0; ) функция возрастает (рис. 4.3, б);
5. График функции y k оси координат не пересекает; x
6.Если k 0 ,то при x 0 функция принимает положительные значения, а при x 0 – отрицательные.
Если k 0, то при x 0 функция принимает отрицательные значения, а при x 0 – положительные;
7.График обратной пропорциональности – гипербола.
26
y |
|
y |
|
y k |
x |
y k x |
|
k 0 |
|||
k 0 |
|
||
|
|
||
0 |
|
x |
|
|
x |
||
|
|
0 |
а |
б |
Рис. 4.3
4.1.4. Функция y x
Основные свойства:
1.Область определения – R ;
2.Область значений – 0; ;
3.Функция четная;
4. Если x 0, то y 0 . Если x 0 , то y 0 . График функции расположен в верхней координатной полуплоскости;
5.Если x 0 , то функция убывает; если x 0, то функция возрастает;
6.График функции – объединение двух лучей: биссектрис первой и второй координатных четвертей (рис.4.4).
y |
y x |
|
x
0
|
|
|
Рис.4.4 |
||||||||
|
4.1.5. Дробно-линейная функция y |
ax b |
|
||||||||
|
cx d |
||||||||||
|
|
|
|
|
|
|
|
||||
|
Основные свойства: |
|
|
|
|
|
|
||||
1. |
Область определения – ( ; |
d |
) ( |
d |
; ) ; |
||||||
c |
|
||||||||||
|
|
|
|
|
|
|
c |
||||
2. |
Область значений - ( ; |
a |
) ( |
a |
; ); |
||||||
|
|
||||||||||
|
|
c |
с |
||||||||
|
|
|
|
|
|
27 |
|
|
|
||
