
- •ВВЕДЕНИЕ
- •ГЛАВА 1. ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ
- •ВЫРАЖЕНИЙ
- •1.1. Многочлены
- •1.1.1. Формулы сокращенного умножения
- •1.1.2. Операции над многочленами одной переменной
- •1.1.3. Корни многочлена
- •1.2. Разложение многочленов на множители
- •1.2.1. Вынесение общего множителя за скобку
- •1.2.2. Способ группировки
- •1.2.3. Использование тождеств сокращенного умножения
- •1.2.4. Разложение многочлена на множители с помощью его корней
- •1.3. Выделение полного квадрата
- •1.4. Многочлены от нескольких переменных
- •1.5. Свойства степени с любым рациональным показателем
- •1.6. Упражнения для самостоятельного выполнения
- •ГЛАВА 2. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА.
- •МЕТОД ИНТЕРВАЛОВ
- •2.1. Задачи для самостоятельного решения
- •ГЛАВА 3. НЕРАВЕНСТВА С МОДУЛЕМ
- •3.1. Задачи для самостоятельного решения
- •ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
- •4.1. Линейные и дробно-линейные функции
- •4.1.1. Прямая пропорциональность
- •4.1.2. Линейная функция
- •4.1.3. Обратная пропорциональность
- •4.2. Квадратичная функция
- •4.3. Степенная функция
- •4.4. Показательная функция
- •4.5. Логарифмическая функция
- •4.6. Тригонометрические функции
- •4.7. Обратные тригонометрические функции
- •4.8. Преобразования графиков функций
- •4.9. Задания для самостоятельного решения
- •ГЛАВА 5. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ
- •5.1. Основные понятия и обозначения
- •5.3. Построение кривых в полярной системе координат
- •5.4. Задания для самостоятельной работы в аудитории
- •ГЛАВА 6. ЛОГАРИФМЫ
- •6.1. Основные свойства логарифмов. Преобразование выражений,
- •содержащих логарифмы
- •6.1.1. Задания для самостоятельного решения
- •6.2. Простейшие логарифмические уравнения и неравенства
- •6.2.1. Задания для самостоятельного решения
- •7.1. Формулы приведения
- •7.2. Основные тригонометрические формулы
- •7.3. Преобразование выражений
- •7.4. Простейшие тригонометрические уравнения
- •7.5. Простейшие тригонометрические неравенства
- •7.6. Задания для самостоятельного решения
- •ГЛАВА 8. КОМПЛЕКСНЫЕ ЧИСЛА
- •8.1. Основные понятия. Алгебраическая форма комплексного числа
- •8.2. Арифметические операции над комплексными числами,
- •заданными в алгебраической форме
- •8.3. Комплексные числа в тригонометрической форме
- •8.3.1. Тригонометрическая форма комплексного числа
- •8.3.2. Действия над комплексными числами в тригонометрической форме
- •8.4. Показательная форма комплексного числа
- •8.5. Задания для самостоятельной работы
- •ГЛАВА 9. ОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКОВ
- •9.1. Понятие определителей второго и третьего порядков
- •9.2. Правила действий над определителями
- •9.3. Задания для самостоятельной работы
- •ГЛАВА 10. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- •10.1. Основные понятия и определения
- •10.2. Линейные операции над векторами
- •10.2.1. Сложение векторов
- •10.2.2. Вычитание векторов
- •10.2.3. Умножение вектора на число
- •10.2.4. Проекция вектора на ось
- •10.2.5. Координаты вектора
- •10.2.6. Направляющие косинусы вектора
- •10.3. Скалярное произведение векторов
- •10.3.1. Свойства скалярного произведения
- •10.4. Векторное произведение векторов
- •10.4.1. Свойства векторного произведения векторов
- •10.5. Смешанное произведение векторов
- •10.5.1. Свойства смешанного произведения
- •10.6. Задания для самостоятельной работы
- •ГЛАВА 11 ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- •11.1. Основные понятия и определения
- •11.1.1. Основные правила дифференцирования
- •11.1.2. Производные основных элементарных функций
- •11.1.3. Производная сложной функции
- •11.2. Задания для самостоятельной работы
- •СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

ГЛАВА 10. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
10.1. Основные понятия и определения
Вектором называется направленный отрезок. Обозначается вектор a или AB ( A – начало вектора, B – его конец).
Нулевым вектором (обозначается 0 ) называется вектор, начало и конец которого совпадают.
Расстояние между началом и концом вектора называется его длиной, или
модулем, или абсолютной величиной (обозначается |
|
|
|
или |
|
|
|
). |
|
|
|
|
|||||
|
a |
|
|
AB |
|
Векторы называются коллинеарными, если они расположены на одной
|
|
|
|
|
|
|
|||
прямой или на параллельных прямых (обозначают a |
|
|
|
b , а также a b , если |
векторы сонаправлены, и a b , если они противоположно направлены).
Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Два вектора называются равными, т.е. a b , если они сонаправлены и имеют равные длины.
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему
10.2. Линейные операции над векторами
Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.
10.2.1. Сложение векторов
Пусть a и b – два произвольных вектора. Возьмем произвольную точку O и построим вектор OA a; затем от точки A отложим вектор AB b. Вектор OB , соединяющий начало первого слагаемого вектора с
концом второго, называется суммой этих векторов и обозначается a b . Ту же сумму можно получить иным способом. Отложим от точки O век-
торы OA a и OB b . Построим на этих векторах как на сторонах парал-
лелограмм OACB . Вектор OC – диагональ параллелограмма – является суммой векторов a и b .
81
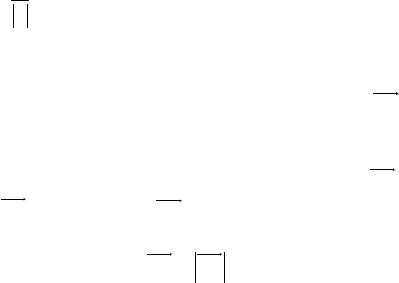
Понятие суммы можно обобщить на случай любого конечного числа слагаемых.
10.2.2. Вычитание векторов
Разностью a b векторов a и b называется такой вектор c , который в сумме с вектором b дает вектор a .
Если векторы a и b привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого»
к«уменьшаемому».
10.2.3.Умножение вектора на число
Произведением вектора a на действительное число называется вектор
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
(обозначают b a ), определяемый следующими условиями: |
|||||||||||||
1) |
|
b |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
a |
|
|
|||||
2) |
|
|
b при 0 |
|
|||||||||
a |
и a b при 0 . |
||||||||||||
Из определения следует: два вектора a и b коллинеарны тогда и только
тогда, когда имеет место равенство b a
Пусть дан вектор a . Ортом вектора a (обозначается ao ) называется вектор единичной длины, сонаправленный с вектором a .
a
Очевидно, ao для любого вектора a . a
10.2.4. Проекция вектора на ось
Пусть дана произвольная ось l и некоторый вектор AB . Опустим из точек A и B перпендикуляры на ось l и обозначим их основания соответственно A1 и B1 .
Длина отрезка A1B1 оси l называется проекцией вектора AB на ось и обо-
значается прl AB . Если вектор AB составляет с осью l угол , то справедлива формула:
прl AB AB cos .
Пример 1. При каком условии на ненулевые векторы a и b справедливо
равенство |
|
|
|
|
|
|
|
? |
|
|
|
|
|||||
|
a b |
|
|
a b |
|
82
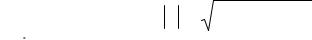
Решение. Отнесем векторы a |
и b к общему началу и построим на них |
|||||||||||||||||
параллелограмм. Тогда |
|
|
|
|
– длина одной диагонали |
этого параллело- |
||||||||||||
|
|
|||||||||||||||||
|
a b |
|
|
|||||||||||||||
грамма, |
|
а |
|
|
|
– |
длина другой диагонали. Диагонали параллелограмма |
|||||||||||
|
|
|
||||||||||||||||
|
|
a b |
|
|||||||||||||||
равны, |
|
если этот |
параллелограмм – прямоугольник. |
Следовательно, |
||||||||||||||
|
|
|
|
|
|
|
, если a перпендикулярен b . |
|
||||||||||
|
|
|
|
|
||||||||||||||
|
a b |
|
|
a b |
|
|
||||||||||||
10.2.5. Координаты вектора
Рассмотрим декартову прямоугольную систему координат Oxyz . Обо-
значим i , j , k – единичные векторы, направленные соответственно вдоль осей Ox , Oy , Oz (орты осей). Эти векторы называются декартовым прямоугольным базисом в пространстве.
Пусть a – произвольный вектор в пространстве. Найдем его проекцию на каждую из координатных осей и обозначим их соответственно ax , ay , az .
Тогда
a axi ay j az k .
Это равенство называется разложением вектора a по базису i , j , k , а числа ax , ay , az называются координатами вектора a в этом базисе, или
декартовыми прямоугольными координатами вектора. Используют обозначение a ax , ay , az .
Таким образом, прямоугольные декартовы координаты вектора – это его проекции на соответствующие оси координат.
Зная координаты вектора, легко выразить его длину:
|
ax2 ay2 az2 . |
a |
Если a AB , где A(xA , yA , zA ) , B(xB , yB , zB ) , то
a xB xA , yB yA , zB zA .
Из свойств проекций (а координаты вектора – это его проекции на оси координат) следует, что, если a ax , ay , az , b bx ,by ,bz , R , то:
1) a b ax bx , ay by , az bz , т.е. равные векторы имеют соответственно равные координаты;
2) a b ax bx , ay by , az bz ;
3) a ax , ay , az – при умножении вектора на число его координаты умножаются на это число;
83
