Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Полная версия Матиматика в вопросах и ответах.pdf

Скачиваний:

Добавлен:

11.03.2016

Размер:

899.46 Кб

Скачать

☆

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 3418 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

1 lg5 1 lg5

lg5

1 lg5 1 lg5

lg5 1 lg5 lg5 1.

lg10 lg5

1 lg5

Ответ. 1.

2 log

3 log

4 log2

Пример 9. Упростить выражение log2

Решение. Получается

полный квадрат

log62 2 2log6 3 log6 2 log62 3

log6 2 log6 3 2

log6

6 2 1.

Ответ. 1.

Пример 10. Доказать тождество aloga b blogd a .

Решение. Приведем левую часть равенства к тому же виду, что и правая его часть:

																					1
																					1
a loga b blogb a loga b																			blogb a					b logb a	что и требовалось доказать.

																							logb a
	6.1.1. Задания для самостоятельного решения
			Вычислить значения выражений:
1)		log					8 log							2 log							25	.			Ответ. 2;
1)		log			5		8 log					5		2 log						5	4	.			Ответ. 2;
					5							5								5	4
2)		log35 7										1						.							Ответ. 1;
2)		log35 7								log5 35								.							Ответ. 1;
						log516				log5 35
3)										2log							3 .								Ответ. –2;
				5
				5												2
4)			lg128						lg81						.										Ответ. – 0,5;
4)															.										Ответ. – 0,5;
			lg4							lg3
5)		21 log							3				.												Ответ. 14.
											7
								7			7
								7

6.2. Простейшие логарифмические уравнения и неравенства

Логарифмическими называются уравнения вида log a f x log a x ,

где a 0, a 1,и уравнения, сводящиеся к уравнениям указанного типа. Замена уравнения log a f x log a x на уравнение f x x называет-

ся потенцированием уравнения. При потенцировании потерять корни нельзя, а можно лишь приобрести посторонние, поэтому, если при решении уравнения пришлось его потенцировать, то в конце решения необходима проверка.

Замена уравнения f x x на уравнение log a f x log a x называ-

ется логарифмированием уравнения. Логарифмировать можно только положительные выражения.

Если проверка корней вызывает затруднение, то необходимо найти ОДЗ (область допустимых значений) уравнения и заменить его равносильной смешанной системой:

loga	f x loga		f x 0		x 0
loga	f x loga	x		или
		f x x		f x x

Любое логарифмическое неравенство сводится в конечном счете к неравенству вида

log a f x log a x ,

где a 0, a 1, при решении, которого используются теоремы равносиль-

ности.
При a 1	При 0 a 1

loga	f x loga	f x x ,	loga	f x loga	f x x ,
		x			x	f x 0.
		x 0.

Пример 1. Решить уравнение 2log2 x log1 2 x 0 .

Решение. Приводим к одному основанию и приравниваем логарифмы log2 x2 log2 1 2 x log2 x2 log2 2 x .

Потенцируем x2 2 x x2 x 2 0. Корни уравнения x1 1 и x2 2 следует проверить, так как не находили ОДЗ. уравнения. После проверки

остается x 1.
Ответ. 1
Пример 2. Решить уравнение log7 2x 5 2 .
Решение.	log7 2x 5 log7	49 2x 5 49 x 22. Корень подходит
при проверке.
Ответ. 22.
Пример 3. Решить уравнение log5 log2 log7 x 0 .
Решение.	По свойствам	log2 log7 x 1 log7	x 2 x 72 . Корень
x 49 подходит при проверке.
Ответ. 49.
Пример 4. Решить уравнение log4 x 2 log1 x 2				1	.
Пример 4. Решить уравнение log4 x 2 log1 x 2					.
			2
		2	2
		54

Решение.

Приводим

логарифмы

одному

основанию

log2 x 2 log2 x 2

log2 x 2

log2 x 2 1

x 2 2 1

x 2

x 2,5 подходит.

Ответ. 2,5.

Пример 5. Найти сумму корней уравнения 2log42 x log4 x 1 0,

ОДЗ: x 0.

Решение.

При замене

log4 x t получаем

квадратное

уравнение

2t2 t 1 0

с корнями t

и t

1) log4 x

x 4 2

2) log4 x 1 x 4 .

Оба корня подходят. Их сумма равна 4

Ответ. 4,5.

Пример 6. Решить неравенство log5 12 3x 1 log5 3.

Решение.

Преобразуем

правую

часть

1 log5 3 log5 5 log5

3 log5 15.

Неравенство равносильно системе

12 3x 0,

x 4,

Ответ. x 1;4 .

12 3x 15

x 1.

Пример 7. Найти сумму целых решений неравенства log1		2x lg1	x 2 .

	3	3

2x 0,

Решение. Равносильная система x 2 0,

2x x 2

x 0,

x 2, 0 x 2 .

x 2

Целые решения x 1 и x 2 . Их сумма равна 3.
Ответ. 3.
Пример		8.	Найти	наименьшее				целое решение неравенства
lg2 x		2	0.
lg2 x	logx 10		0.
	logx 10		x 0,
			x 0,
Решение. Найдем ОДЗ x 1,							x 0, x 1.
			log		x	10 0
					x
Перейдем			к основанию 10				и	обозначим	lg x t , тогда

lg2 x 2lg x 0 t2 2t 0, t t 2 0 t 0	или t 2. Для нахождения
55

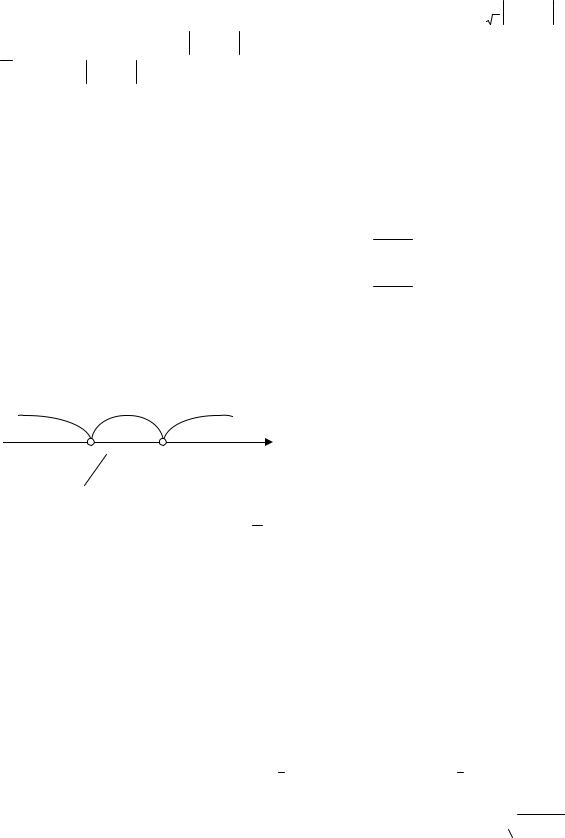
x получим lg x 0 x 1 или lg x 2 x 100 . Учитывая ОДЗ, получим решение x 0;1 100; .

Пример 9. Найти наименьшее решение неравенства log 2 2x 3 0. Ре-

шение. Находим ОДЗ 2x 3 0 2x 3 0, x 1,5, так как основание

2 1, то 2x 3 1 1 2x 3 1 2 x 1. С учетом ОДЗ решением является x 2; 1,5 1,5; 1 . Наименьшим числом в решении является –2.

Ответ.– 2.

Пример. 10. Решить неравенство log2	x 3		1.

		4 x

Решение. Решаем равносильную систему


нения			второго неравенства. Решим
	x 3	2 0		3x 5	0 .

	4 x			4 x

x 3

4 x 0, Достаточно выпол-x 3 2.

4 x

его методом интервалов.

–

5 4

Неравенство выполняется при 5 x 4 . 3

5
Ответ.		;4	.
	3

6.2.1. Задания для самостоятельного решения

Пример 1. Найти сумму корней уравнения log3 x 2 log5 x 7 log3 x 2 .

Ответ. –1.

Пример 2. Решить уравнение. log1 2x 5 log7 6 log1 2 .

Ответ. 3,5.

Пример 3. Найти произведение корней уравнения 2log4 x log4 x 1 0.

Ответ. 4.

Пример 4.		Найти число корней уравнения log2		x 6	1	log	2 x .
Пример 4.		Найти число корней уравнения log2		x 6		log	2 x .
Ответ. 1.				2
Ответ. 1.
Пример 5.		Найти сумму целых решений неравенства
log1 2x 3 log1 3x 2 .
	2		2

Ответ. 8.

Пример 6. Найти число целых решений неравенства log3 x 7 log3 5 x log1 3 x .

Ответ. 7.			3
Ответ. 7.
Пример		7.	Найти наименьшее натуральное решение неравенства
log1	x 7		0.

	2x 5

5

Ответ. 8.

Пример 8. Найти наибольшее целое решение неравенства log0,3 x2 3x 12 log0,3 9 x

Ответ. 8

Пример 9. Найти сумму целых решений неравенства log22 x 3log2 x 2 0

Ответ. 9.

Пример 10. Решить неравенство log1	x 2		1	.


		2

9
Ответ. x 5; 2 2;1 .

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 3418 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.11.2019261.63 Кб3Полит ПР спецкурс.doc
#
28.03.201525.4 Кб14политика предприятия.docx
#
27.03.2015168.96 Кб12политическая идеалогия.doc
#
14.04.201930.98 Кб3Политология (Вопросы 1-5).docx
#
27.12.2019182.27 Кб0политология.doc
#
11.03.2016899.46 Кб65Полная версия Матиматика в вопросах и ответах.pdf
#
28.03.201566.75 Кб4Положение Конкурса IT-VOLGA.docx
#
16.02.2020861.66 Кб0полупроводники.docx
#
11.01.2020916.48 Кб0Полупроводниковые диоды.doc
#
16.09.2019114.18 Кб6Понятие социальной стратификации.doc
#
26.11.20191.32 Mб4Попова лаба хорошая.docx

6.1.1. Задания для самостоятельного решения

6.2. Простейшие логарифмические уравнения и неравенства

6.2.1. Задания для самостоятельного решения