4.2. Кибернетика второго порядка
Это направление развития кибернетики (неклассической) оформилось в связи с появлением исследований по самоорганизации, изучению и моделированию мозга, искусственного интеллекта и других разработок.
Понятие самоорганизации возникло во многих отраслях знаний, не только в кибернетике и поначалу было достаточно разноречиво, оставаясь таковым во многом еще и сегодня.
В рамках классической кибернетики этим явлением занимался прежде всего английский ученый У .P. Эшби [4]. Он выделил два различных значения термина "самоорганизующаяся система". Во-первых, самоорганизация может состоять в переходе от системы с независимыми частями к системе с зависящими друг от друга частями, при этом не учитывается, хороша или плоха возникающая организация. Во-вторых, самоорганизацией можно считать переход от плохой организации к хорошей, когда, например, ребенок, вначале потянувшись к огню, затем уже избегает его.
Системы, целевая функция которых связывалась с адаптацией к окружающей среде, стали называть "адаптивными". Для создания искусственной адаптивной системы существовало два способа: сконструировать систему сразу в окончательном виде или построить начальный вариант, снабдив его возможностями развития адаптивных свойств. В последнем случае систему называли "обучающейся". Обучение происходило либо с внешним "учителем", либо самостоятельно, за счет обратной связи ("самообучение").
В соответствии с кибернетическим принципом "черного ящика" все эти характеристики относились исключительно к поведению (внешним проявлениям) системы. Улучшение поведения (достижение адаптивности) понималось в кибернетике как переход от плохой организации системы к хорошей, и этот процесс стали называть "самоорганизацией".
Один из возможных критериев адаптации — устойчивость системы относительно некоторого состояния равновесия. Этот принцип был положен Эшби в основу специального устройства — гомеостата, который осуществляет самоорганизацию второго типа его классификации. Гомеостатический принцип Эшби распространил и на высшую нервную деятельность. Он предположил, что гомеостазис является основным механизмом работы мозга. К этой группе относится и самообучающаяся машина. Такие системы стали называть обучающимися, но не самосвязующимися.
Ко второму типу систем, в которых элементы первоначально не были связаны, а в результате обучения и самоорганизации связываются, можно отнести персептрон, предложенный Ф. Pозенблатом, предназначенный для распознавания реальных зрительных образов, в частности печатных букв. Основу персептрона составляли сеть нейроноподобных элементов и "система управления поощрением", которая сравнивала стимул с реакцией системы и изменяла соответствующим образом веса "полезных" и "вредных" связей.
Pазрабатываемые системы искусственного интеллекта также можно отнести к самоорганизующимся системам, например, таким, как система "Эвриско" Лената и др.
В итоге Эшби считает самоорганизующейся системой комплексную систему, состоящую из машины, в которой осуществляется самоорганизация, и управляющей машины, которая осуществляет этот процесс.
Классическое понимание "управления в животном и машине" как централизованной, иерархической структуры, где информация "снизу" поступает лишь как конечный результат по каналу обратной связи, а решение принимается только "наверху", оказалось неспособным ни отразить сложность функционирования реальных систем, ни дать модели для построения интеллектуальных машин, современных систем управления.
Требовались иное понимание самоорганизации, иные подходы, неклассические. Как ни парадоксально, но во второй половине 50-х годов таким "неклассиком" стал именно основатель классической кибернетики Hорберт Винер.
Pечь идет о системах, в которых нет явно выраженного управляющего центра, органа, подсистемы, но которые, тем не менее, удивительно самоорганизуются.
Такие явления Винер наблюдал при исследовании электроэнцефалограмм человеческого мозга, при формировании сосудистой системы зародыша позвоночного, когда образуются определенные сократительные клетки, которые вскоре уже составляют сердце с регулярным биением, при анализе синхронной работы генераторов в электроэнергетической системе.
Винер видел, что самообращенный характер связи элементов системы становится источником их согласованного действия, "...реакция нелинейной системы на случайные входы дает нам ключ к способности физиологических процессов организовываться в определенную синергетическую деятельность".
Дальнейшее развитие кибернетики связано с изучением явления самоорганизации и развитием соответствующего понятия в самых различных областях знаний, относящихся как к живым, так и неживым системам [5]. И хотя это понятие еще не выработано достаточно однозначно, тем не менее можно сформулировать его следующим образом: под самоорганизацией понимаются процессы упорядочивания, происходящие в системе за счет действия ее составляющих. При этом существенно, что эта система открыта, нелинейна, сильно неравновесна, с диссипацией (рассеиванием) энергии во внешнюю среду, система потокового типа — с притоком и оттоком энергии, вещества.
В отличие от структурирования типа кристаллизации, происходящего в закрытой системе и вблизи от состояния термодинамического равновесия, самоорганизация обеспечивается взаимодействиями внутри системы, находящейся в "возбужденном", неравновесном состоянии. Кроме того, существенно, что самоорганизация не навязывается системе извне: хотя она инициируется какими-то внешними воздействиями, эти воздействия не являются, так сказать, специфичными, формообразующими.
Примерами самоорганизации могут служить процессы соединения птиц в стаю, людей на улице в очередь у магазина, предпринимателей в ассоциацию, ячейки Бенара (структурирование подогреваемой жидкости в виде маленьких водоворотов "конвективных валов", с параллельными горизонтальными осями), "химические часы" (колебание концентрации раствора) и др.
В самоорганизующихся системах происходят очень сложные процессы, при изучении которых необходимо прежде всего учитывать следующие.
- Различие между актуальной, проявляющей себя в пространстве и времени структурой, параметры которой можно наблюдать и измерять, и потенциальной (нереализованной в данное время) структурой, не имеющей пространственно-временных свойств и, следовательно, не наблюдаемой непосредственно, но оказывающей воздействие на процесс в целом. Основное свойство потенциальной структуры — альтернативность, т.е. наличие исключающих друг друга (при реализации) состояний. Они могут быть состояниями равновесия или неравновесия, регулярными или случайными процессами разной длительности, самоподдерживающимися, самоускоряющимися, самозамедляющимися или переходными процессами.
При определенных условиях какая-то из этих альтернатив приобретает устойчивость и реализуется, заменив ставшее неустойчивым прежнее состояние ("обмен устойчивостью"). "Обмен устойчивостью" может быть связан с рождением новых или исчезновением ряда прежних альтернатив. Эти альтернативы определяют, чем данная система может стать при тех или иных условиях и чем она не сможет быть никогда (ни при каких условиях).
- Наличие особой области значений параметров, в которой малые внешние воздействия на систему могут вызвать в ней значительные изменения, в том числе структурные (эффект самоорганизации). Значения параметров в этой области называют критическими.
- Неопределенность поведения системы при критических значениях параметров, означающая отсутствие каких-либо правил, позволяющих по данному состоянию системы и совокупности всех воздействий на нее однозначно или с некоторой вычислимой вероятностью определить ее следующее (будущее) состояние. В этих условиях система или процесс обладают внутренней свободой, позволяющей им спонтанно (без внешней причины) формировать свои новые состояния.
Когда значения параметров близки к критическим, то достаточно малого воздействия на систему, чтобы она скачком перешла из данного (существующего в настоящий момент времени) состояния, ставшего неустойчивым, в новое устойчивое состояние, изменив способ поведения.
В области критических значений параметров системы или процесса флуктуации (неустремимые малые случайные колебания) могут нарастать, вызывая хаос.
Поведение системы становится случайным, непредсказуемым и неуправляемым.
Самоорганизация систем или процессов возникает при определенных граничных и начальных условиях спонтанно в виде особых состояний либо как следствие особых состояний, называемых еще аттракторами в теории динамических систем и в синэнергетике. Слово "аттрактор" подчеркивает эффект притягивания системы к особому, устойчивому состоянию. В основе этих явлений лежит согласованное поведение большого числа взаимодействующих подсистем. Термин "синэнергетика" означает совместное действие.
Переходя к кибернетике второго порядка, можно сказать, что она ставит задачу изучения процессов в таких сложных, неравновесных, нелинейных, динамичных системах с целью управления происходящими там процессами [6].
Здесь, так же как и в классической кибернетике, используется инструмент, понятие обратной связи. Но если в классической кибернетике объектом являются саморегулируемые устойчивые системы, изучаемые в рамках общей модели в виде объекта управления, регулятора и отрицательной обратной связи, уменьшающей отклонения системы от установившегося или желаемого состояния, то в кибернетике второго порядка используется инструмент положительной обратной связи, которая усиливает отклонения от исходного состояния опять-таки для достижения желаемого в динамически эволюционизирующейся системе.
Общей чертой этих двух моделей является наличие взаимообусловливающих внутренних элементов, которые воздействуют друг на друга. Если отклонение погашается, значит, результирующая обратная связь отрицательна, система поддерживает заданное ей входным сигналом состояние и является объектом изучения классической кибернетики. Изучением же взаимообусловливающих процессов, усиливающих отклонения, занимается кибернетика второго порядка.
Процессы первого типа по предложению М. Маруяма, называют "морфостазисом", а второго типа — "морфогенезисом".
В системах второго типа небольшое первоначальное отклонение, имеющее высокую вероятность, развивается в отклонения с очень редкой вероятностью. Для иллюстрации этого можно привести много примеров, в частности, возникновение города в земледельческой местности. Когда один из фермеров открывает лавку и начинает продавать инструменты, она становится местом встречи фермеров. Поэтому там вскоре открывается продовольственный магазин, растет поселок, расширяется торговля сельскохозяйственными продуктами, возникает промышленность и появляется город. Первоначальный толчок, породивший в итоге город, с большей вероятностью мог произойти на любой из ферм, разбросанных по данной равнине. Здесь сработал случай, но затем образование цепей с положительными обратными связями с необходимостью порождает такое сложное образование, как город.
Кибернетика второго рода находится, по существу, в стадии становления, постановки целей, задач ее, выработки подходов.
Один из подходов — это уже упоминавшийся подход М. Маруяма, основанный на выявлении циклов в сложной системе, состоящей из взаимодействующих элементов, и оценивании количественных характеристик этих взаимодействий. Такой подход открывает перспективы для моделирования динамики, для анализа динамики и жизнеспособности. Именно в этом смысле кибернетика второго порядка полезна для изучения социальных, биологических систем как автономных и операционально-замкнутых.
Однако возникает вопрос: какова цель такого изучения системы? Ответом могло быть то, что подход, основанный на описанных циклах взаимодействий, уже используется для разработки систем поддержки решений при управлении крупными фирмами и корпорациями и, прежде всего, для выработки стратегических решений, связанных с их развитием, эволюцией, меняющих их структуру, что является основным условием выживания организации.
Но как только мы ввели управляющий орган, то сразу наша система вышла из ранга самоорганизующихся и перешла в ранг управляемых.
В итоге граница между кибернетиками первого и второго порядка определяется:
а) видом обратных связей в системах (отрицательные — классическая кибернетика, положительные — второго порядка);
б) местом управляющего органа. Если в классической кибернетике управляющая подсистема и управляемый объект разделены и противопоставлены друг другу, то в кибернетике второго порядка предполагается, что управление неотделимо от системы, связано с ней сложной сетью взаимодействий, и можно сказать, что управляющий орган управляет собой в составе системы (рис.4.4). В этом плане понимание управления очень близко (если не тождественно) с пониманием управления в мыследеятельностном подходе.
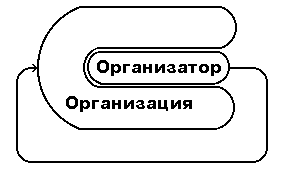
Рис.4.4