Дробно-линей пр

§ 2.4. ЗАДАЧИ ДРОБНО-ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

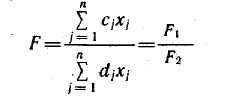(89)

1. Экономическая и геометрическая интерпретации задачи дробно-линейного программирования. Общая задача дробно-линейного программирования состоит в определении максимального значения функции

при условиях

(90)

(91)

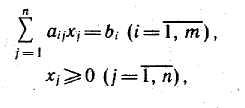
где — некоторые постоянные числа, в области неотрицательных решений си­стемы линейных уравнений (90). При этом будем предполагать, что (> 0 (такое условие не нарушает общности задачи, поскольку в том случае, когда эта величина отрицательна, знак минус можно отнести к числителю).

Как и в случае основной задачи линейного программирова­ния, свое максимальное значение целевая функция задачи (89) — (91) принимает в одной из вершин многогранника решений, опре­деляемой системой ограничений (90) и (91) (естественно, при условии, что эта задача имеет оптимальный план). Если макси­мальное значение целевая функция задачи (89) принимает бо­лее чем в одной вершине многогранника решений, то она дости­гает его также во всякой точке, являющейся выпуклой комби­нацией данных вершин.

Рассмотрим задачу, состоящую в определении максималь­ного значения функции

(92)

при условиях

Будем считать, что

Чтобы найти решение задачи (92) — (94), как и в § 1.3 при рассмотрении задачи (19) —(21), сначала находим многоуголь­ник решений, определяемый ограничениями (93) и (94). Предполагая, что этот многоугольник не пуст,, полагаем значение функции равным некоторому числу Л, так что прямая

проходящая через начало координат, имеет общие точки с мно­гоугольником решений. Вращая построенную прямую (95) вокруг начала координат, либо определяем вершину (вершины), в кото­рой функция (92) принимает максимальное значение, либо уста­навливаем неограниченность функции на множестве планов за­дачи.

Итак, процесс нахождения решения задачи (92) — (94) вклю­чает следующие этапы:

1. В системе ограничений задачи заменяют знаки неравенств на знаки точных равенств и строят определяемые этими равенствами прямые.

2. Находят полуплоскости, определяемые каждым из неравенств системы ограничений задачи.

3. Находят многоугольник решений задачи.

4. Строят прямую (95), уравнение которой получается, если положить значение целевой функции (92) равным некоторому постоянному числу.

5. Определяют точку максимума или устанавливают неразрешимость задачи.

6. Находят значение целевой функции в точке максимума.

2.77. Для производства двух видов изделий А и В предприя­тие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов обору­дования. Время обработки каждого из изделий на оборудовании данного типа приведено в табл. 2.50. В ней же указаны затраты, связанные с производством одного изделия каждого вида.

Таблица 2.50

Тип оборудования	Затраты времени (ч) на обработку одного изделия
	А	В
I II III	2 1 12	8 1 3
Затраты на производство одного изделия (руб)	2	3

Оборудование I и III типов предприятие, может использовать не более 26 и 39 ч. При этом оборудование II типа целесообраз­но использовать не менее 4 ч.

Требуется определить, сколько изделий каждого вида следует изготовить предприятию, чтобы себестоимость одного изделия была минимальной.

Решение. Предположим, что предприятие изготовит х₁ изделий вида А и х₂ изделий вида В. Тогда общие затраты на их производство равны руб., а себестоимость одного изде­лия в рублях составит

Затраты времени на обработку указанного количества изде­лий на каждом из типов оборудования соответственно составят часов, часов и часов. Так как оборудо­вание I и III типов может быть занято обработкой изделий вида А и В не более 26 и 39 ч, а оборудование II типа — не менее 4 ч, то должны выполняться следующие неравенства:

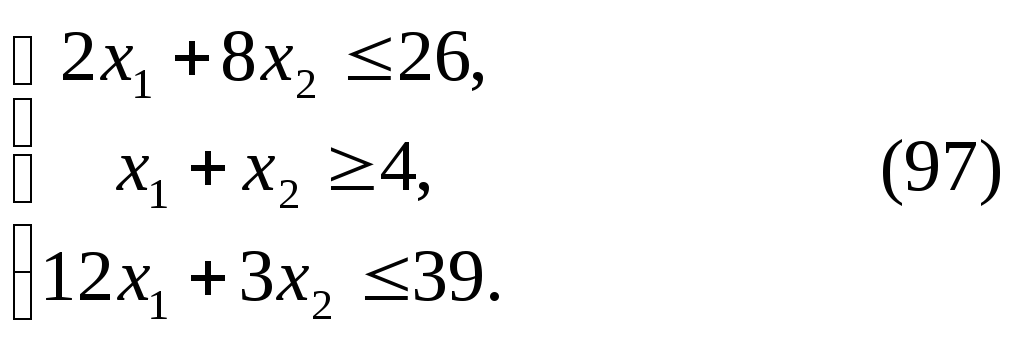
По своему экономическому смыслу переменные *i и х₂ могут принимать только лишь неотрицательные значения:

Таким образом, математическая постановка задачи состоит в определении неотрицательного решения системы линейных не­равенств (97), реализующего минимум функции (96). Чтобы найти решение задачи, прежде всего построим многоугольник решений. Как видно из рис. 2.8, им является треугольник BCD. Значит, функция (96) принимает минимальное значение в одной из точек: В, С или D. Чтобы определить, в какой именно, положим значение функции F равным некоторому числу, например 11/4.

Тогда

или

Уравнение, (99) определяет прямую, проходящую через на­чало координат. Координаты точек, принадлежащих этой прямой и многоугольнику решений, являются планами задачи, при кото­рых значение функции (96) равно 11/4. В данном случае к ука­занным точкам относится лишь одна точка В (1; 3). Ее коорди­наты определяют план задачи, при котором значение функции равно 11/4.

Рис. 2.8

Возьмем теперь h = 5/2, т.е. положим

или

'

Уравнение (100), так же как и (99), определяет прямую, проходящую через начало координат. Ее можно рассматривать как прямую, полученную в результате вращения по часовой стрелке вокруг начала координат прямой (99). При этом коорди­наты точек, принадлежащих прямой (100) и многоугольнику решений, являются планами задачи, при которых значение функции (96), равное 5/2, меньше, чем в точках прямой (99),. Следовательно, если положить значение функции (96) равным некоторому числу h_о:

а прямую (101), проходящую через начало координат, вращать в направлении движения часовой стрелки вокруг начала координат, то получим прямые

Найдем последнюю общую точку вращаемой прямой с много­угольником решений. Это точка D (3; 1) (рис. 2.8), в которой достигается минимум функции (96).

Таким образом, оптимальным планом производства продукции является план, согласно которому изготовляется три изделия вида А и одно изделие вида В. При таком плане себестоимость одного изделия является минимальной и равна

При нахождении угловой точки многоугольника решений, в которой целевая функция задачи принимает наименьшее значе­ние, мы полагали значение функции равным некоторым двум по­стоянным числам и установили направление вращения прямой, определяющее уменьшение значения функции. Это можно было сделать и по-другому. А именно: полагая значение функции F равным некоторому числу h, т.е.

и получив некоторую прямую, проходящую через начало коорди­нат и имеющую угловой коэффициент, зависящий от h, можно, используя производную, установить направление вращения пря­мой (102) при возрастании h.

Практически же дело обстоит гораздо проще. Найдя точки В (1; 3) и D (3; 1) (рис. 2.8), в которых функция (96) может при­нимать минимальное значение, вычислим ее значения в этих точках: F (В)=11/4, F (D)=9/4. Так как F (B) > F (D), то можно утверждать, что в точке D целевая функция принимает мини­мальное значение. Одновременно с этим заметим, что в точке В функция F принимает максимальное значение.

Заканчивая рассмотрение нахождения решения задачи дроб­но-линейного программирования графическим методом, отметим, что при решении конкретных задач могут быть различные случаи.

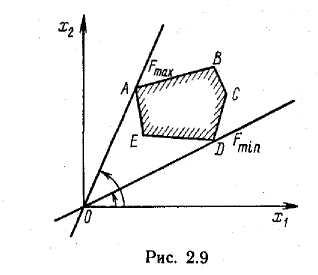
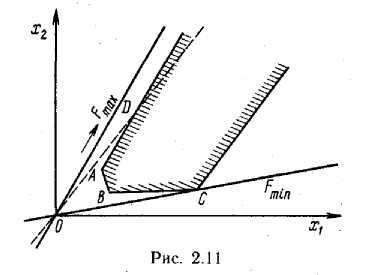
1. Многогранник решений ограничен, максимум и минимум достигаются в его угловых точках (рис. 2.9).

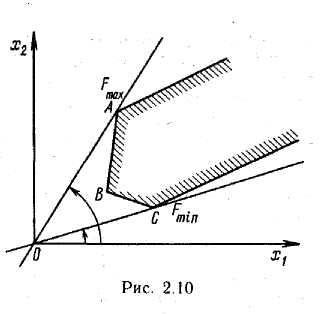
2. Многогранник решений не ограничен, однако существуют угловые точки, в которых целевая функция задачи принимает соответственно максимальное и минимальное значения (рис. 2.10)

3. Многогранник решений не ограничен, и один из экстремумов достигается. Например, минимум достигается в одной из вершин многогранника решений и функция F имеет так называе­мый асимптотический максимум (рис. 2.11).

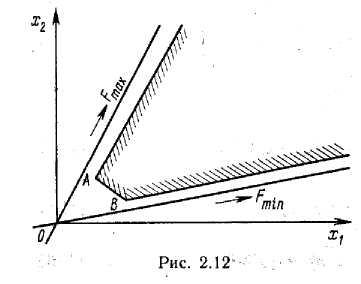
4. Многогранник решений не ограничен, как максимум, так и минимум являются асимптотическими (рис. 2.12).

Используя геометрическую интерпретацию задачи дробно-линейного программирования, найдите решение задач 2.78—2.80.

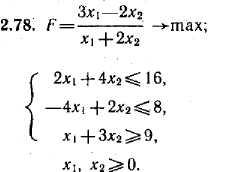
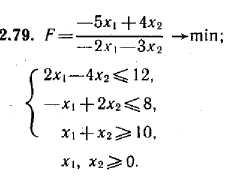
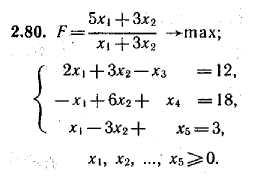
Составьте математические модели задач 2.81—2.83. и решите симплексным методом.

81. Для производства n видов изделий предприятие использует m типов взаимозаменяемого оборудования. Каждый из видов изделий необходимо изготовить в количестве b_i единиц 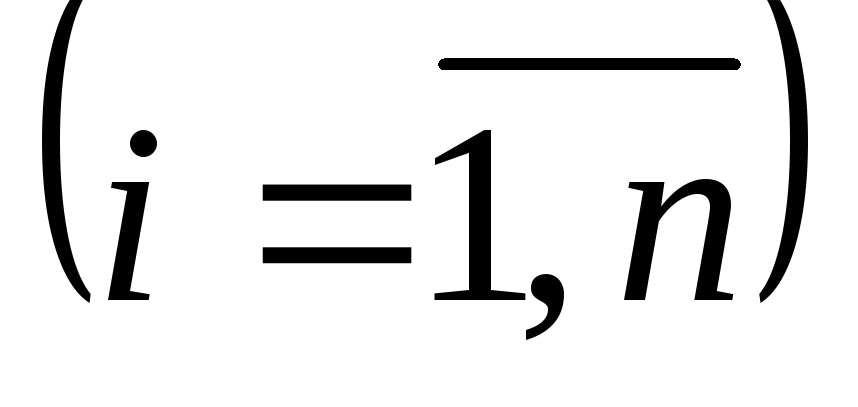, причем каждый из типов оборудования может быть занят изготовлением этих изделий не больше чем а_j часов 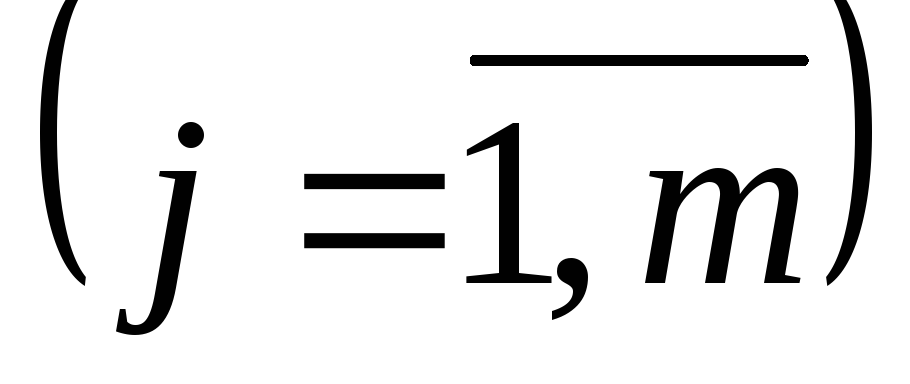. Время изготовления одного изделия i-ro вида на j-м типе оборудования равно a_ij- часам, а затраты, связанные с производством одного изделия на данном типе оборудования, равны c_ij руб. Определить, сколько изделий каждого вида на каждом из типов оборудования следует произвести так, чтобы себестоимость одного изделия была минимальной.

82. Обувное производственное объединение для изготовления n различных моделей обуви использует т видов кожтоваров. На изготовление одной пары обуви j-й 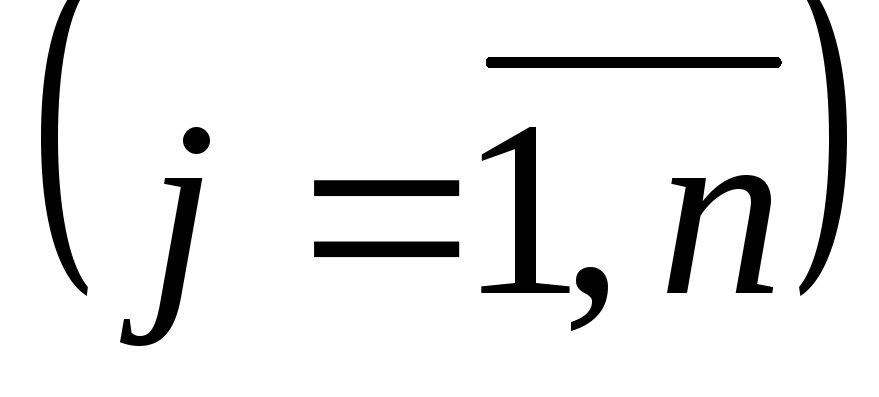модели требуется а_ij м² кожтоваров i-ro вида 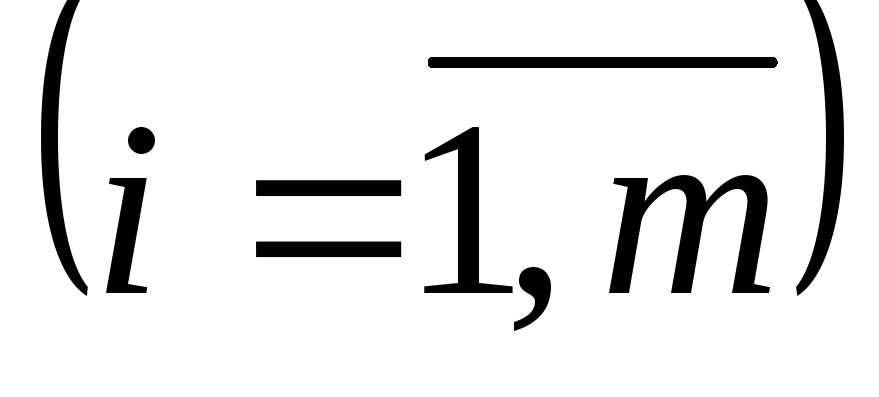, а всего их может быть использовано b_i м². Величина производственных фондов, используемых при производстве одной пары обуви j-й модели, равна c_j руб., а прибыль от реализации равна dj руб. •Предполагая, что объединение может выпускать обувь разных моделей в любых соотношениях, найти план выпуска, обеспечивающий максимальную рентабельность.

83. Для выполнения п различных работ могут быть использованы рабочие т квалификационных групп. При выполнении j-й работы i-й группой рабочих выработка в единицу времени равна с_ij 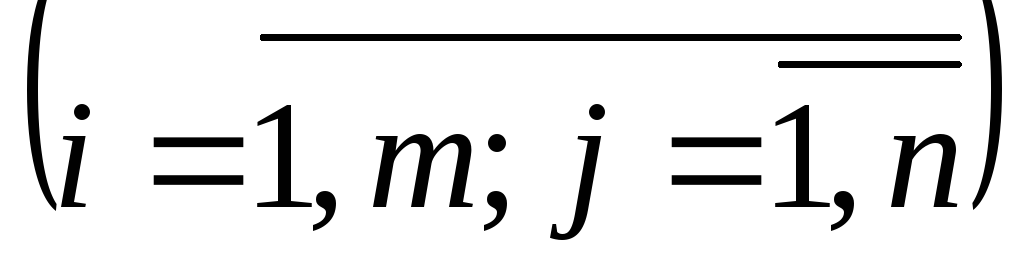руб. Общий фонд времени, в течение которого i-я группа рабочих может быть занята выполнением работ, не превышает b₁, единиц времени, а объем j-й работы равен a_j- руб. Составить такой план выполнения работ, при котором производительность труда является максимальной.

2. Сведение задачи дробно-линейного программирования к задаче линейного программирования. Сформулированная выше задача (92) — (94) может быть сведена к задаче линейного про­граммирования. Для этого следует обозначить

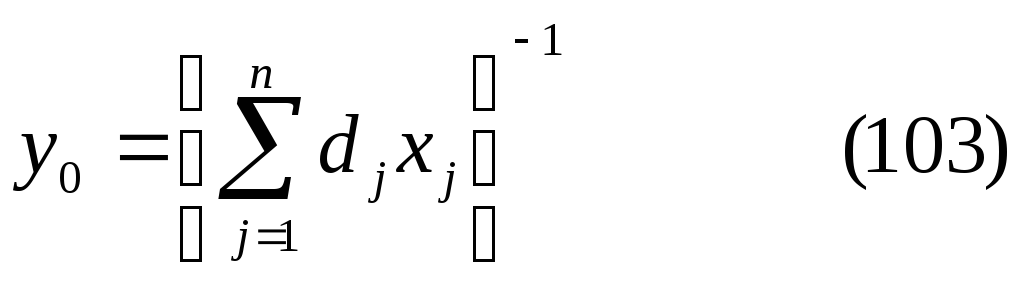
и ввести новые переменные

Используя введенные обозначения, исходную задачу (92) — (94) сведем к следующей: найти максимум функции

при условиях

Задача (105) — (108) является задачей линейного програм­мирования, а следовательно, ее решение можно найти извест­ными методами. Зная оптимальный план этой задачи, на основе соотношений (104) получаем оптимальный план исходной задачи (92)-(94).

Таким образом, процесс нахождения решения задачи дробно-линейного программирования включает следующие этапы:

1. Сводят задачу (92) — (94) к задаче линейного программирования _(Ш>) — (Ю8).

1. Находят решение задачи (105) — (108).

2. Используя соотношения (104), определяют оптимальный план задачи (92) — (94) и находят максимальное значение функции (92).

84. Найти максимальное значение функции

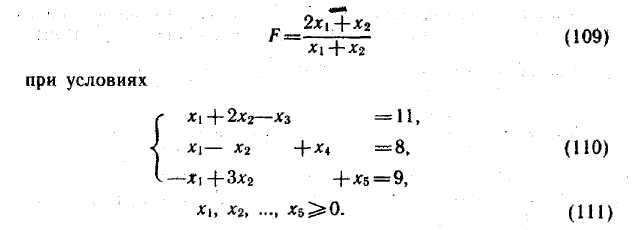
Решение. Сведем данную задачу к задаче линейного про­граммирования. Для этого обозначим через y₀ и вве­дем новые переменные . В результате приходим к следующей задаче: найти максимум функции

при условиях

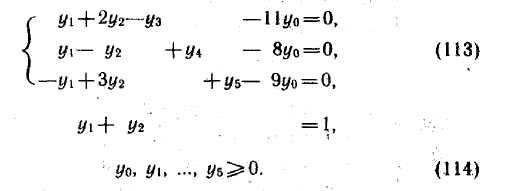
Задача (112) — (114.) является задачей линейного програм­мирования. Ее решение находим методом искусственного базиса (табл. 2.51).

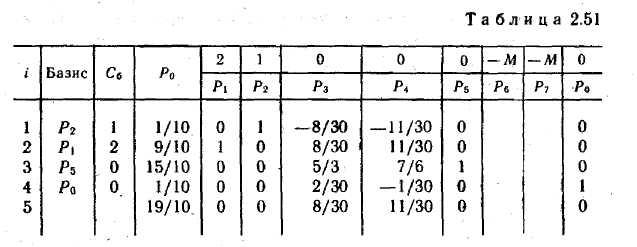
Из табл. 2.51 видно, что оптимальным планом задачи {112) — (114) является

Учитывая, что , находим оптимальный план задачи (109) —(111): Х^*=(9; 1; 0; 15). При этом плане F_max=19/10.

Найдите решение задач 2.85—2.89.