ЛЕКЦИИ ПО ГЕОДЕЗИИзаочное-ускоренное (1)
.docВопрос №25
Уравнения поправок
Мы знаем, что не существует универсального способа решения систем нелинейных уравнений, поэтому уравнения связи приводят к линейному виду. В линейном виде они называются уравнениями поправок.
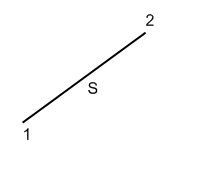
В общем виде S=![]()
Пункты 1 и 2 являются определяемыми и между ними измерена сторона S
Заданная приближенными значениями
координат определяемых пунктов X![]() ,
Y
,
Y![]()
![]() и
X
и
X![]() ,
Y
,
Y![]() .
Измеренные значения стороны обозначим
через S, после уравнивания
должно выполняться следующее равенство:
.
Измеренные значения стороны обозначим
через S, после уравнивания
должно выполняться следующее равенство:
S+V=![]()
![]()
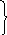 ,
,
![]()
![]() ,
,
![]()
- поправки в приближенных значения координат определяемых пунктов
Для приведения данного уравнения к линейному виду разложим его в ряд Тейлора:
f(x+![]() x)=f(x)+
x)=f(x)+![]()
![]()
S+V=![]()
Обозначим
![]() за S
за S![]()
![]()
![]()
![]()
![]()
С другими производными поступаем также:
S+V=S![]() -
-![]()
V=-![]()
L=S![]() -S
-S
Вопрос №26
Уравнения поправок направлений
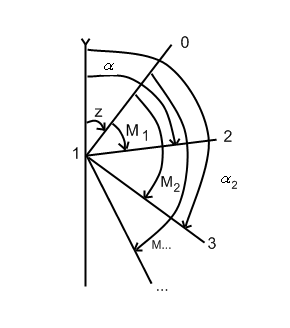
Измеряются направления М![]() ,
М
,
М![]() .
.
Z – дирекционный угол нулевого направления, его называют ориентирующим углом.
Можно записать, что
![]() ;
;
![]() …,
где
…,
где
![]() - дирекционные углы направлений.
- дирекционные углы направлений.
В общем случае можно записать
![]()
M=-z+![]()
Из геодезии известно, что
![]() ,
значит
,
значит
М=-z+![]() - это уравнений является исходным для
составления уравнений поправок
направлений.
- это уравнений является исходным для
составления уравнений поправок
направлений.
Зададимся приближенными значениями
![]()
M+V=-
Разложим это уравнение в ряд Тейлора:
M+V=

Найдем одну из производных
Пусть
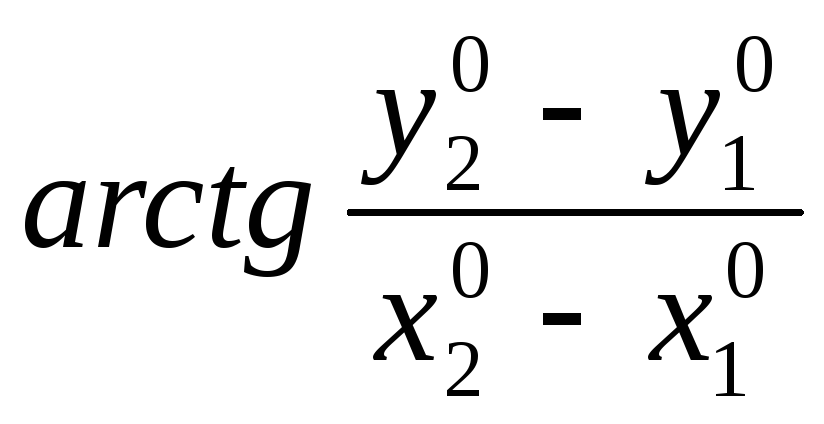 =
=![]()

Упрощаем:
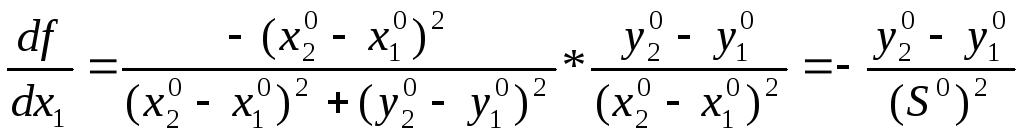 ,
а
,
а
![]() ,
тогда
,
тогда
![]() (также и остальные производные)
(также и остальные производные)
M+V=-![]()
V=![]() ,
где
,
где
L=![]()
Вопрос №27
Уравнение поправок GPS измерений и превышений
![]()
![]()
![]()
Рассмотрим уравнивание на примере Δх:
Зададимся:
![]() ,
,
![]()
![]()
![]() ,
где
,
где![]()
![]()
![]()

![]()
Вопрос №28
Решение уравнений поправок по МНК
Проиллюстрируем на примере трех уравнений с двумя неизвестными.
П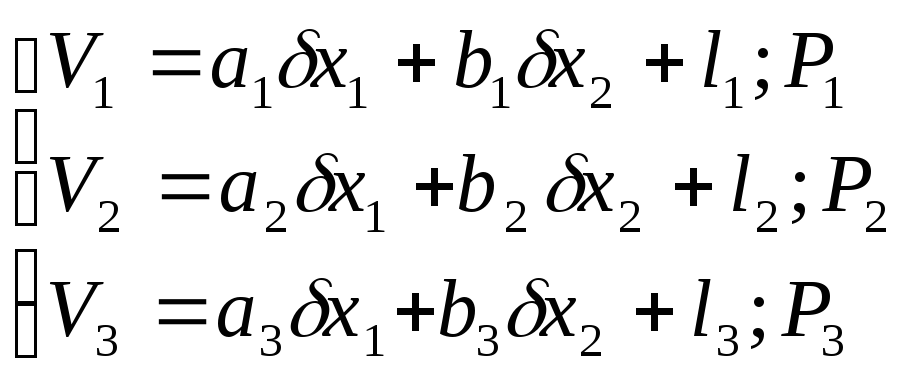 усть
каждое уравнение имеет свой вес Р1,
Р2, Р3
усть
каждое уравнение имеет свой вес Р1,
Р2, Р3
![]()
![]()
Сущность метода наименьших квадратов заключается в том, что
Ф=![]()
Вес – это величина обратная:
![]()
Ф=![]()
Ф=![]()
Чтобы Ф было минимальным необходимо:
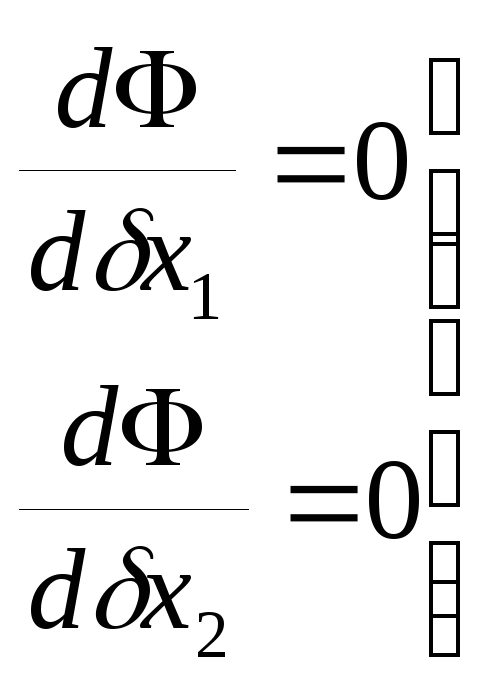 условия
экстремума
условия
экстремума
![]()
![]()
![]()
![]() - складываем столбиком
- складываем столбиком
Так же делаем для
![]()
Таким образом получится система:
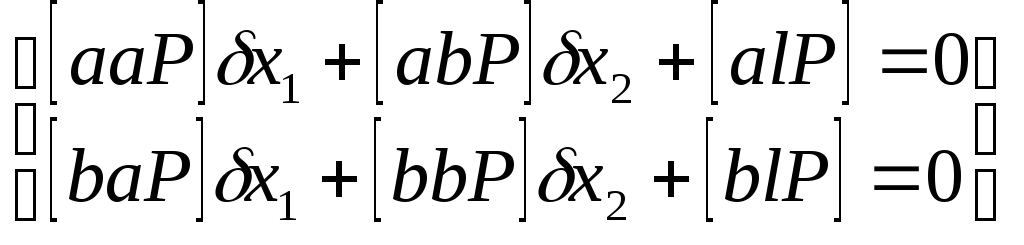 - это есть система нормальных уравнений
- это есть система нормальных уравнений
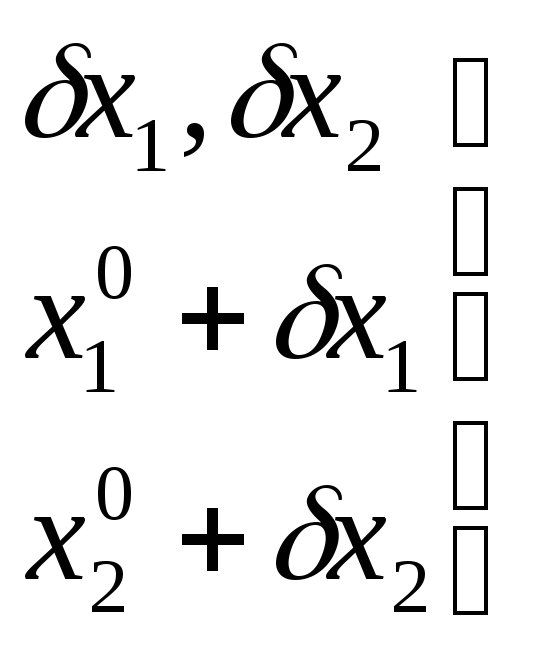 - находятся из системы нормальных
уравнений
- находятся из системы нормальных
уравнений
I Решение уравнений по схеме Гаусса:
Из первого уравнения находим
![]() :
:
![]()
Подставим во второе уравнение:
![]()
После при ведения подобных слагаемых получим следующий вид:
![]()
Вводим соответствующие обозначения:
![]()
![]()
Таким образом вместо исходной системы уравнений решается следующая:
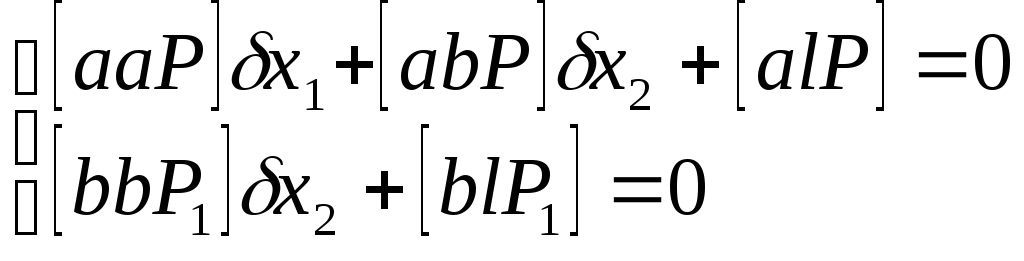
-
находим из второго уравнения:

-
находим
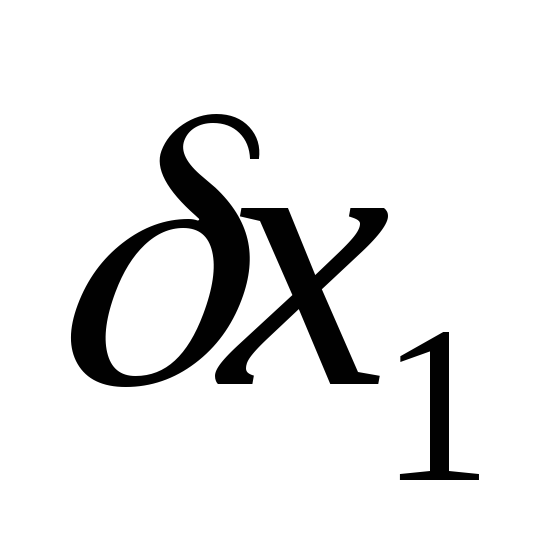 подставляя
подставляя
 в
первое уравнение
в
первое уравнение
Пример уравнения геодезических сетей параметрическим способом
Пусть ГС GPS – методом измерены приращения координат.
|
|
|
|
|
|
![]() направления
измерения приращения координат
направления
измерения приращения координат
Относительно исходных пунктов ABC
по измеренным приращениям координат
![]() необходимо
вычислить координаты точек 1 и 2.
необходимо
вычислить координаты точек 1 и 2.
Задачу будем решать раздельно, по каждой оси координат.
Выполним выравнивание по оси OX.
Порядок уравнивания следующий:
1. Вычисляем приближенные координаты, определяемых точек сети:
![]()
![]()
2. Составляем систему уравнений поправок. Уравнений будет столько, сколько имеется измерений (4).
На основе положений в общем виде запишем уравнение поправок для всех 4 измерений.
![]()
![]()
![]()
![]()
Таблица уравнений поправок
|
№ измерения |
|
|
L |
P |
V |
|
1 |
+1 |
0 |
0 |
1 |
-0.01 |
|
2 |
-1 |
0 |
0 |
1 |
+0.01 |
|
3 |
-1 |
+1 |
-0.05 |
1 |
-0.02 |
|
4 |
0 |
-1 |
0 |
1 |
-0.02 |
3. Составляем таблицу
нормальных уравнений
![]()
|
|
|
|
|
3 |
-1 |
0,05 |
|
|
2 |
-0,05 |
4. Решение системы по схеме Гаусса
|
|
|
|
|
+3 |
-1 |
0,05 |
|
-1 |
+0,33 |
-0,017 |
Всю строку делим на диагональный элемент, умножаем на элемент строки, стоящий справа.
|
|
2 |
-0,05 |
|
|
-0,33 |
+0,017 |
|
|
+1,67 |
-0,033 |
|
|
-1 |
+0,02 |
![]()
![]()
Окончательные значения:
![]()
![]()
5. Вычисляем поправки
![]()
![]()
![]()
![]()
Вопрос №29
Решение уравнений поправок по МНК в матричном виде
Исходная система уравнений поправок:
V=AX+L
![]()
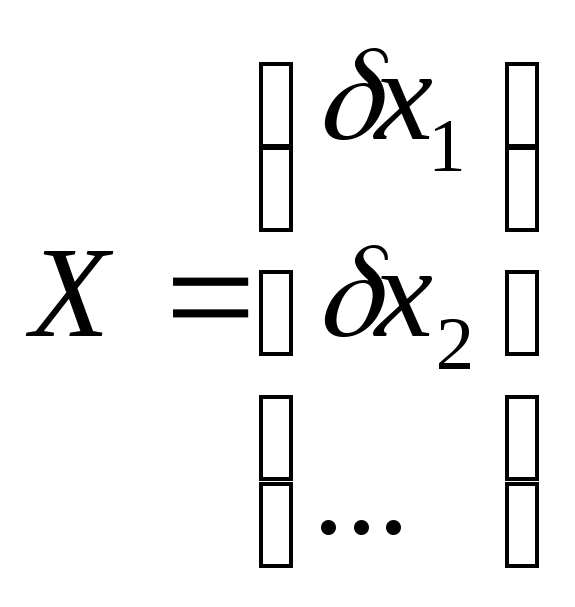
![]()
 a1 b1
…
a1 b1
…
A= a2 b2 …
a3 b3 …

P1
P= P2
P3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Для решения умножаем на обратную матрицу слева:
![]()
![]()
![]()
Вопрос №30
Обращение матрицы методом Жордана.
![]()
 разрешающий элемент
разрешающий элемент
-
Выбираем разрешающий элемент и заменяем обратной величиной.
-
Остальные элементы разрешающей строки делятся на разрешающий элемент.
-
Остальные элементы разрешающего столбца делятся на разрешающий элемент и заменяют знаки на противоположные.
-
Остальные элементы вычисляются по правилу прямоугольника.
-
 = 0,2
= 0,2 -
 = 0,4
= 0,4 -
-
 = - 0,4
= - 0,4 -
6
 –
– 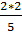 = 5,2
= 5,2
0,2 0,4
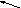 - 0,4 5,2 разрешающий элемент
- 0,4 5,2 разрешающий элемент
Делаем следующий шаг Джордановых исключений, но разрешающим будет уже следующий элемент.
-
 = 0,18
= 0,18 -
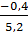 = - 0,08
= - 0,08 -
–
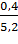 = 0,08
= 0,08 -
0
 ,2
–
,2
– 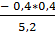 = 0,23
= 0,23
0,23 - 0,08
- 0,08 0,18
Контроль


 0,23 - 0,08 * 5 2 = 1 0
0,23 - 0,08 * 5 2 = 1 0
- 0,08 0,18 2 6 0 1
Вопрос №31
№ 31. Виды условных уравнений.
Базируется на условных уравнениях, составляемых в сети. Число условных уравнений ГС равно числу избыточных измерений.
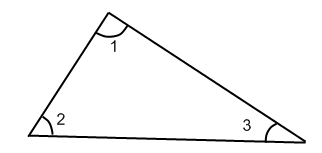
3-е измерение избыточное - оно позволяет контролировать
1. Процесс измерений
2. Повышать точность измерений
3. Оценивать точность измерений.
Всякие невязки при обработке теодолитных ходов и иных геодезических построений позволяет оценивать точность выполняемых работ.
В данном построении возможно уравнивание
фигур, согласно которому сумма углов
в треугольнике должна равняться 180![]() .
.
1+(1)+2+(2)+3+(3)-180![]() =0
=0
(1), (2), (3) – поправки
1+2+3+W=0, где W=1+2+3-180![]()
W – свободный член условного уравнения равный невязке.
В триангуляции еще возможны условные уравнения к базису.
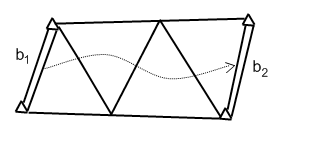
Исходя из базиса
![]() ,
мы должны получить базис
,
мы должны получить базис
![]() .
Расхождение между вычисленным базисом
и заданным свидетельствует о точности
измерений и является свободным членом
базисного условного уравнения.
.
Расхождение между вычисленным базисом
и заданным свидетельствует о точности
измерений и является свободным членом
базисного условного уравнения.
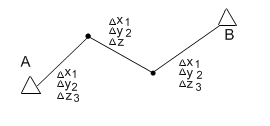
Условные уравнения будут иметь вид:
![]() )=
)=![]()
![]()
![]()
![]()
![]()
![]()

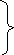
![]()
![]()
![]()
Из решения условных уравнений необходимо найти поправки к измерениям.
Вопрос №32
Решение условных уравнений по МНК
Проиллюстрируем на примере двух условных уравнений.
![]()

![]()
Ф=![]()
Поскольку, здесь поправки связаны условными уравнениями, то записывается задача на условный экстремум.
Для решения задачи записывается функционал Лагранша.
Ф=![]()
Найдем отсюда поправки, для этого найдем:
![]() =0
=0
![]()
![]()
Отсюда:
![]()
![]()
![]()
Здесь неизвестны множители Лагранша.
![]() - корелантны
- корелантны
Найдем их, подставив поправки
![]() в условные уравнения.
в условные уравнения.
Покажем подстановку на примере 1-го уранения.
![]()
![]()
![]()
![]() W
W![]()
![]()
-![]()
-![]()
Из решения этих 2-х уравнений находим
координаты k![]() ,
,![]() ,
а потом и поправки
,
а потом и поправки
![]() .
.
Вопрос №33
Уравнивание коррелатным способом в матричном виде
Покажем коррелатный способ уравнивания в матричном виде:
B*V+W=0

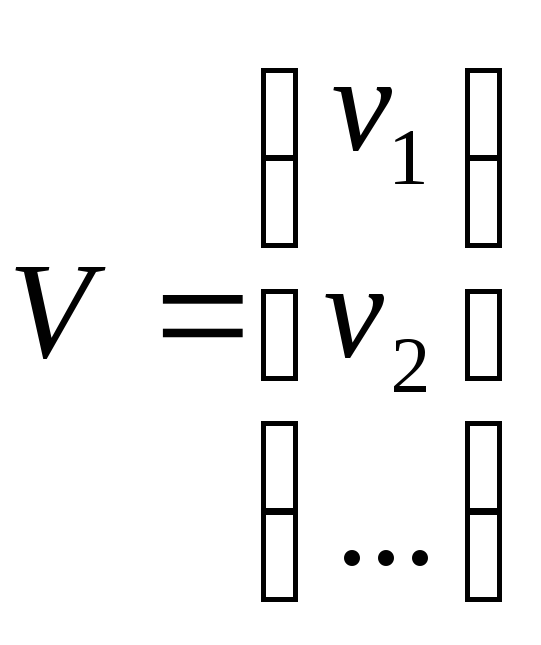
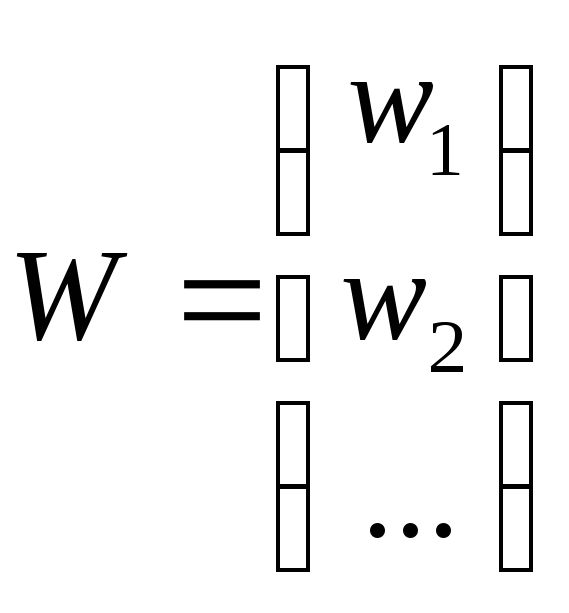
![]() =VTPV+2KT(BV+W)=минимально,
где КТ=(К1 К2….)
=VTPV+2KT(BV+W)=минимально,
где КТ=(К1 К2….)
![]() =2VTP+2KT*B=0
=2VTP+2KT*B=0
VT=-KTBP-1
V=-(KTBP-1)=P-1BTK
B*P-1BTK+W=0
N=BP-1BT
NK+W=0
K= -N-1W
Порядок уравнивания:
1. Составляем систему условных уравнений:
B*V+W=0
2. Составляем и решаем системы нормальных уравнений:
K=-N-1W
3. Находим поправки:
V=P-1BTK
4. Считаем поправки:
V1=K1*a1+K2*a2